Решение:

A11 = (-1)1 + 1·M11 = (-1)2·

1 0 0 3

= 1·3 - 0·0 = 3 - 0 = 3

A12 = (-1)1 + 2·M12 = (-1)3·

-4 0 2 3

= -(-4·3 - 0·2) = -(-12 -0) = 12

A13 = (-1)1 + 3·M13 = (-1)4·

-4 1 2 0

= -4·0 - 1·2 = 0 - 2 = -2

A21 = (-1)2 + 1·M21 = (-1)3·

7 1 0 3

= -(7·3 - 1·0) = -(21 - 0) = -21

A22 = (-1)2 + 2·M22 = (-1)4·

5 1 2 3

= 5·3 - 1·2 = 15 - 2 = 13

A23 = (-1)2 + 3·M23 = (-1)5·

5 7 2 0

= -(5·0 - 7·2) = -(0 - 14) = 14

A31 = (-1)3 + 1·M31 = (-1)4·

7 1 1 0

= 7·0 - 1·1 = 0 - 1 = -1

A32 = (-1)3 + 2·M32 = (-1)5·

5 1 -4 0

= -(5·0 - 1·(-4)) = -(0 + 4) = -4

A33 = (-1)3 + 3·M33 = (-1)6·

5 7 -4 1

= 5·1 - 7·(-4) = 5 + 28 = 33

Теорема Лапласа

Теорема 1. (Теорема Лапласа) Зафиксируем в квадратной матрице произвольные строк с номерами . Тогда определитель матрицы равен сумме произведений всевозможных миноров, построенных на этих строках, на их алгебраическое дополнение. То есть .

Если зафиксировать в матрице только одну строку с номером , то, как частный случай из теоремы Лапласа, получим следующую формулу: .

Пример 6. Вычислим определитель матрицы из примера 3 с помощью разложения по первой строке: .

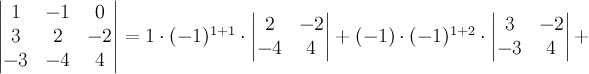
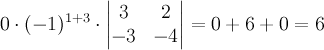Теорема Лапласа

Теорема

Пусть - определитель -го порядка. Выберем в нем произвольные строк (или столбцов), причем . Тогда сумма произведений всех миноров -го порядка, которые содержатся в выбранных строках (столбцах), на их алгебраические дополнения равна определителю.

Пример

Задание. Используя теорему Лапласа, вычислить определитель

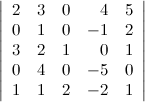
Решение. Выберем в данном определителе пятого порядка две строки - вторую и третью, тогда получаем (слагаемые, которые равны нулю, опускаем):

Ответ.

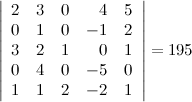
Вопрос 4

mathprofi.ru›Действия с матрицами

Матрицы и действия над ними.

Рассмотрим матрицу вида:

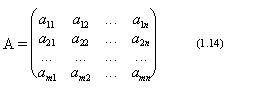
Можно пользоваться сокращенной формой записи:

A = ( a_ij ); i = 1, 2, 3, .... , m ; j = 1, 2, 3, ....., n .

О. Нулевой матрицей называется матрица все элементы которой равны 0.

О. Две матрицы одинаковой размерности mxn называются равными, если на пересечении i-й строки и j-го столбца в одной и в другой матрице стоит одно и то же число; i=1, 2, ..., m ; j=1, 2, ..., n .

Пусть A = (a_ij) – некоторая матрица и g–произвольное число,тогда g A = (g a_ij), то есть при умножении матрицы A на число g все числа, составляющие матрицу A, умножаются на число g.

Пусть A и B – матрицы одинаковой размерности A = (a_ij), B = (b_ij), тогда их сумма A + B – матрица C = (c_ij) той же размерности, опреде­ляемая из формулы c_ij = a_ij + b_ij, то есть при сложении двух матриц попарно складываются одинаково расположенные в них числа.

Матрицу A можно умножить на матрицу B, то есть найти матрицу C = AB, если число столбцов n матрицы A равно числу строк матрицы B, при этом матрица C будет иметь столько строк, сколько строк у матрицы A и столько столбцов, сколько столбцов у матрицы B. Каждый элемент матрицы C определяется формулой

Элемент c_ij матрицы-произведения C равен сумме произведений элементов i -строки первой матрицы- сомножителя на соответствующие элементы j -го столбца второй матрицы - сомножителя.

Таким образом, формула (1.16) является записью системы m линейных уравнений с n неизвестными в матричной форме. Ниже будет показано, что, записывая систему в сжатом виде, кроме краткости написания мы получаем и другие очень важные преимущества.

Пусть имеются две квадратные матрицы А и В одинаковой размерности.

Требуется найти матрицу X, удовлетворяющую матричному уравнению

AX = В.

О. Обратной матрицей к матрице A называется такая матрица A^–1, для которой справедливы равенства:

AA ^–1 = A ^–1 A = E (1.17)

Очевидно, что A^–1 – квадратная матрица того же размера, что и матрица A. Сразу заметим, что не всякая квадратная матрица имеет обратную матрицу. Матрица А имеет обратную матрицу, если detA не равно 0.

Обратная матрица имеет вид:

5 вопрос

Обратная матрица

Высшая математика Гусак стр.115-118 Или

На множестве матриц не определена операция деления, она заменена умножением на обратную матрицу.

Определение

Невырожденной называется квадратная матрица, определитель которой не равен нулю. Квадратная матрица называется вырожденной, если ее определитель равен нулю.

Квадратная матрица называется обратной к невырожденной матрице , если , где - это единичная матрица соответствующего порядка.

Замечание

Обратная матрица существует только для квадратных матриц с не равными нулю определителями.

Свойства обратной матрицы:

1°   

2°   

3°   

4°   

Нахождение обратной матрицы с помощью присоединённой матрицы

Теорема

Если к квадратной матрице дописать справа единичную матрицу того же порядка и с помощью элементарных преобразований над строками добиться того, чтобы начальная матрица, стоящая в левой части, стала единичной, то полученная справа будет обратной к исходной.

Пример

Задание. Для матрицы найти обратную методом присоединенной матрицы.

Решение. Приписываем к заданной матрице справа единичную матрицу второго порядка:

От первой строки отнимаем вторую (для этого от элемента первой строки отнимаем соответствующий элемент второй строки):

От второй строки отнимаем две первых:

Первую и вторую строки меняем местами:

От второй строки отнимаем две первых:

Вторую строку умножаем на (-1), а к первой строке прибавляем вторую:

Итак, слева получили единичную матрицу, а значит матрица, стоящая в правой части (справа от вертикальной черты), является обратной к исходной.

Таким образом, получаем, что

Ответ.

Замечание

Если на некотором этапе в "левой" матрице получается нулевая строка, то это означает, что исходная матрица обратной не имеет.

Облегченный способ для матрицы второго порядка

Для матрицы второго порядка можно немного облегчить нахождение обратной, используя следующий алгоритм:

Шаг 1. Находим определитель заданной матрицы, если он равен нулю, то делаем вывод, что обратной матрицы не существует, иначе переходим к следующему шагу.

Шаг 2. Элементы, стоящие на главной диагонали меняем местами, а у элементов побочной диагонали меняем знак на противоположный.

Шаг 3. Делим все элементы на и получаем обратную матрицу.

Пример

Задание. Найти обратную матрицу для

Решение. Шаг 1. , тогда обратной матрицы не существует.

Ответ. Так как определитель матрицы равен нулю, то она не имеет обратной.

Пример

Задание. Найти обратную матрицу для

Решение. Шаг 1. Находим определитель:

Шаг 2.

Шаг 3.

Ответ.

Нахождение обратной матрицы с помощью союзной матрицы

Определение

Матрица называется союзной к квадратной матрице , если элементы матрицы равны алгебраическим дополнениям соответствующих элементов матрицы .

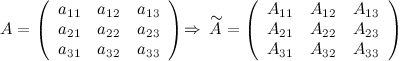
Имеет место следующее свойство:

Тогда, если , то , а тогда

Таким образом, матрица имеет союзную тогда и только тогда, когда она невырожденная.

Пример

Задание. Найти обратную матрицу к матрице

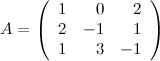
Решение. Вычисляем определитель матрицы:

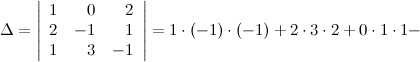
Так как определитель не равен нулю, то матрица имеет обратную. Обратная матрица к матрице находится по формуле:

Найдем союзную матрицу , для этого вычислим алгебраические дополнения к элементам матрицы :

Таким образом,

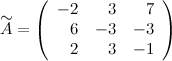
Транспонируем эту матрицу (т.е. строки матрицы делаем столбцами с тем же номером):

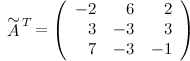
Итак,

Ответ.