1 Вопрос Высшая математика Гусак стр.104-111 Или
Определители 2-го и 3-го порядков linal.ru›opredeliteli-2-go-i-3-go-poryadkov/
Определители 2-го и 3-го порядка появились в связи с решением систем линейных уравнений 2-го и 3-го порядков. Этот факт мы будем наблюдать при изучении определителей произвольного порядка. В настоящем параграфе рассматриваются только формальные правила вычисления определителей 2-го и 3-го порядков: этого будет достаточно при изучении векторного произведения двух векторов, а также в некоторых геометрических задачах на плоскости и в пространстве.
Определители 2-го порядка.
Определителем
2-го порядка
называют число, представленное в виде
специальной конструкции:
=
,
которой ставят в соответствие число:
.
Записывают:
= = . (1)
Говорят, что правая часть выражения (1) определяет правило его вычисления определителя 2-го порядка.
При использовании определителя применяют термины:
элементы определителя – числа a11, a12, a21, a22;
строки определителя: 1-я строка: пара чисел: a11,a12 , 2-я строка: пара чисел a21,a22;
столбцы определителя: 1-й столбец: пара чисел: a11,a21, 2-й столбец: пара чисел a12,a22;
члены определителя: (a11·a22) и (–a21·a12).
При внимательном рассмотрении соответствия (1) нетрудно заметить правило использования элементов определителя для записи суммы левой части выражения (1). Для записи положительного члена определителя (a11·a22) используют схему:
Для записи отрицательного члена определителя (–a21·a12) используют схему:
Рассмотрим несколько примеров вычисления определителей 2-го порядка, использующих в качестве своих элементов числа, или некоторые аналитические выражения.
Пример
В–02:
Вычислить определитель 2-го порядка:
d=
.
Решение:
1). Воспользуемся общей формулой: = .
2). В нашем примере: d=(-1)·2–(-5)·4 = 18.
Ответ: d=18.
Пример
В–03:
Вычислить определитель 2-го порядка:
d=
.
Решение:
1). Воспользуемся общей формулой: = .
2).
В нашем примере: d=(a+b)·(a+b)–(a–b)·(a–b) =
.
Ответ: d = .
Замечание: формальное применение правила вычисления определителей 2-го порядка не вызывает никаких затруднений!
Определители 3-го порядка.
Определителем
3-го порядка
называют число, представленное в виде
специальной конструкции:
=
,
которой ставят в соответствие число,
определяемое суммой, составленной из
шести слагаемых (членов определителя):
=
+
+
–
–
–
. (2)
Говорят, что правая часть выражения (2) определяет правило его вычисления определителя 3-го порядка. Соответствие, представленное выражением (2), легко запоминается, если использовать геометрическую схему составления членов определителя:
Рассмотрим несколько примеров вычисления определителей 3-го порядка, использующих в качестве своих элементов числа, или некоторые аналитические выражения.
Пример
В–04: Вычислить определитель 3-го порядка:
=
.
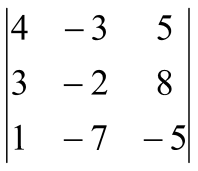Решение:
Вычислим определитель, применяя правило (2) и учитывая принятые обозначения:
= + + – – – , или:
=
=100.
Ответ: d = 100.
Пример
В–05: Вычислить определитель 3-го порядка:
=
.
Решение:
Вычислим определитель, применяя правило (2) и учитывая принятые обозначения:
= + + – – – , или:
=
=1.
Ответ: d = 1.
Оказывается, есть правило сведения вычисления определителя 3-го порядка к вычислению нескольких определителей 2-го порядка, а именно:
=
= 
–
+
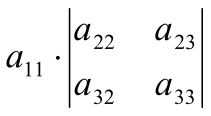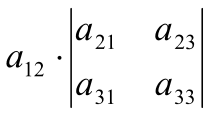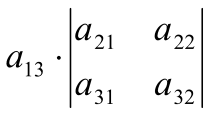, (3)
или
=
=
–
+
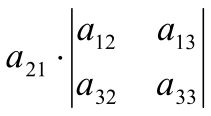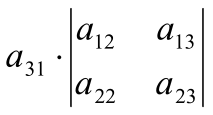, (4)
Обоснование
правил (3) и (4) вычисления определителя
3-го порядка мы получим в теории
определителей
-
го порядка.
Замечание: правило (3) называют: вычисление определителя разложением по первой строке, а правило (4): разложение по первому столбцу.
Рассмотрим несколько примеров вычисления определителей 3-го порядка, использующих в качестве своих элементов числа, или некоторые аналитические выражения.
Пример В–06: Вычислить определитель 3-го порядка: d= .
Решение:
Вычислим определитель тремя способами: сначала применим правило (2), затем правило (3) и правило (4).
Способ 1. В соответствии с определением определителя 3-го порядка:
= + + – – – , или:
=100.
Способ 2. В соответствии с правилом (3) вычислим определитель 3-го порядка разложением по 1-й строке:
= = – + , или
=100.
Способ 3. В соответствии с правилом (4) вычислим определитель 3-го порядка разложением по первому столбцу:
= = – + , или
=100.
Ответ: d = 100.