Точечные и интервальные оценки параметров распределения по данным выборки.

Точечная оценка – оценка, даваемая одним числом (точкой на числовой оси), которому приближенно равна оцениваемая характеристика.

Генеральное среднее (Х)

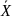= 1/N ∑ х_i

Оценкой генерального среднего является выборочное среднее.

= 1/n ∑ m_i x_i

Генеральная дисперсия:

α = 1/N ∑ (x_i – X)²

Выборочная дисперсия:

S² = 1/n ∑ m_i (x_i – x)²

Оценкой генеральной дисперсии является выборочная дисперсия. Наилучшей оценкой генеральной дисперсии является исправленная выборочная дисперсия.

Исправленная выборочная дисперсия:

S²= 1/n-1 ∑ m_i (x_i – x)²

Если объем выборки меньше или равен тридцати, то пользуются исправленной выборочной дисперсией; если же объем больше тридцати, то можно пользоваться просто формулой для выборочной дисперсии. Наилучшей оценкой для генерального среднего квадратического отклонения является выборочное среднее квадратическое отклонение, равное корню квадратному из выборочной дисперсии.

Интервальные оценки.

Чтобы дать представление о точности и надежности полученной оценки (точечной) используют доверительные интервалы и доверительные вероятности, то есть ответ задается в виде интервала на числовой оси.

Доверительным называется интервал, который с заранее заданной надежностью гамма покрывает оцениваемый параметр. Это может использоваться для оценки мат. ожидания случайной величины Х, распределенной по нормальному закону при известном среднем квадратическом отклонении.

Надежность (доверительная вероятность) обозначается буквой гамма – это степень уверенности в том, что доверительный интервал будет содержать истинное значение параметра Х (среднее) генеральной совокупности. Традиционно значение гамма берут равным 95% и по этому значению находят ширину доверительного интервала.

Распределение Стьюдента:

Пусть величина Ч имеет нормальное распределение. Уильям Госсек исследовал свойства величины Т.

Т = (Х –х)/ S_x

Величина Т отражает связь между отклонением Х от х и среднеквадратическим отклонением с учетом объема выборки. Сейчас говорят, что величина Т подчиняется распределению Стьюдента, свойства которого нам известны. Тогда обозначив, дельта х полуширину доверительного интервала, мы можем записать формулу Стьюдента.

При этом учитывается число степеней свободы f = n – 1

(табл. 2)

Из генеральной совокупности извлечена выборка объема 50, после анализа выборки был построен ряд распределения. Оценить с надежностью 95% математическое ожидание величины х, если мы считаем, что х распределена нормально. Находим точечную оценку х (среднее) и находим среднее квадратическое отклонение.

Для нормального распределения известно, какая часть совокупности попадает в любой интервал вокруг среднего значения:

67% всех выборочных средних попадут в интервал ±S

95% в интервал ±2S

97% в интервал ±3S

Последовательность действий при построении доверительного интервала:

1. По выборке вычисляются х и s

2. Выбирается доверительная вероятность у подсчитывается f и соответствующее им значение параметра t

3. Вычисляется дельта х

4. Строится интервал х± дельта х

Определение объема репрезентативной выборки

T = (Δх корень из n)/S

n – необходимый объем выборки для того, чтобы выборка была репрезентативной.

В этой формуле S получается из анализа предварительной выборки (пробной) и неизвестна заранее, поэтому такое исследование является двухэтапным.