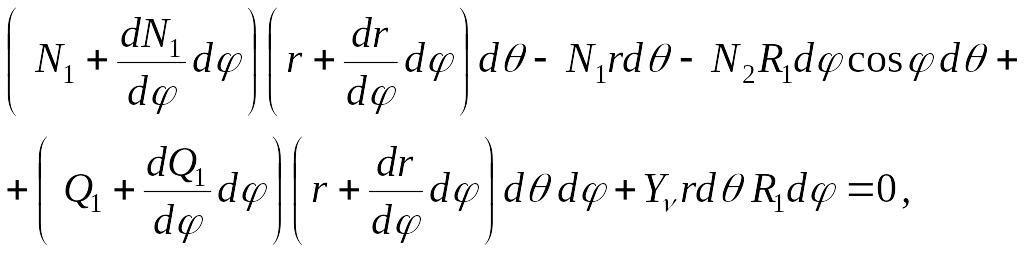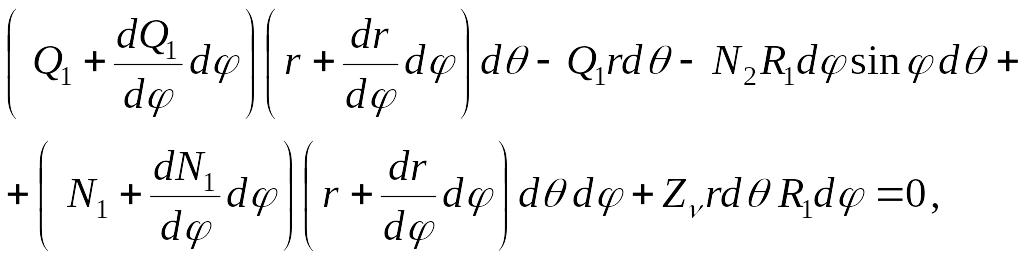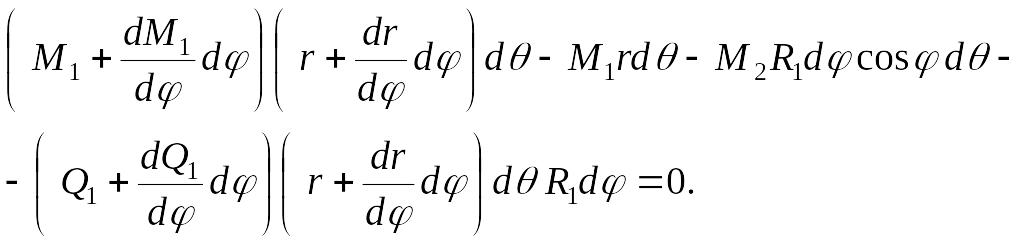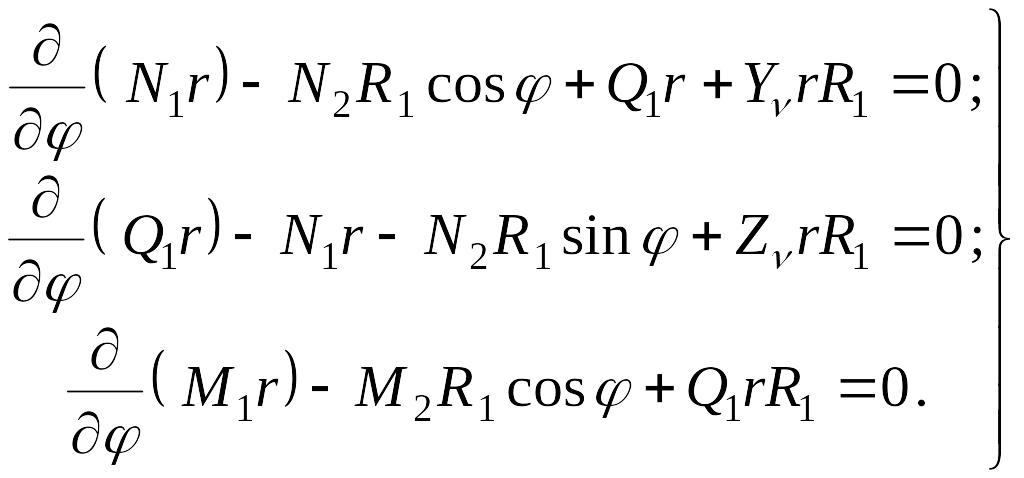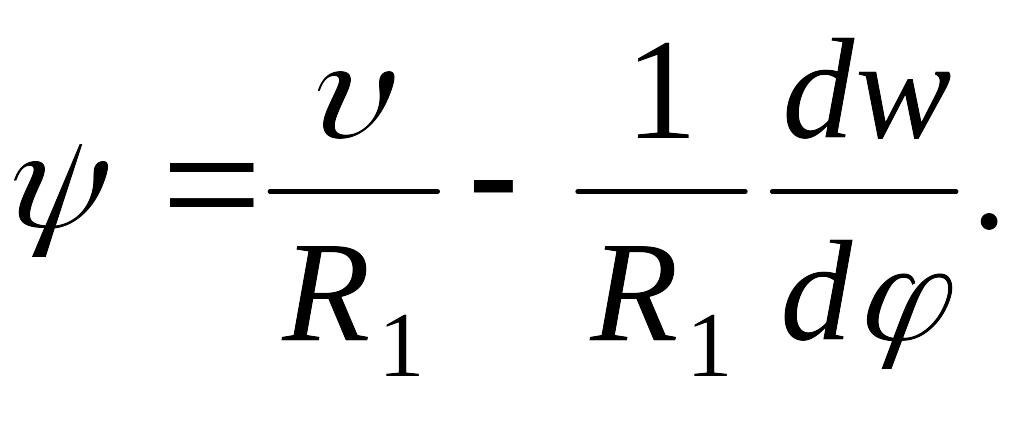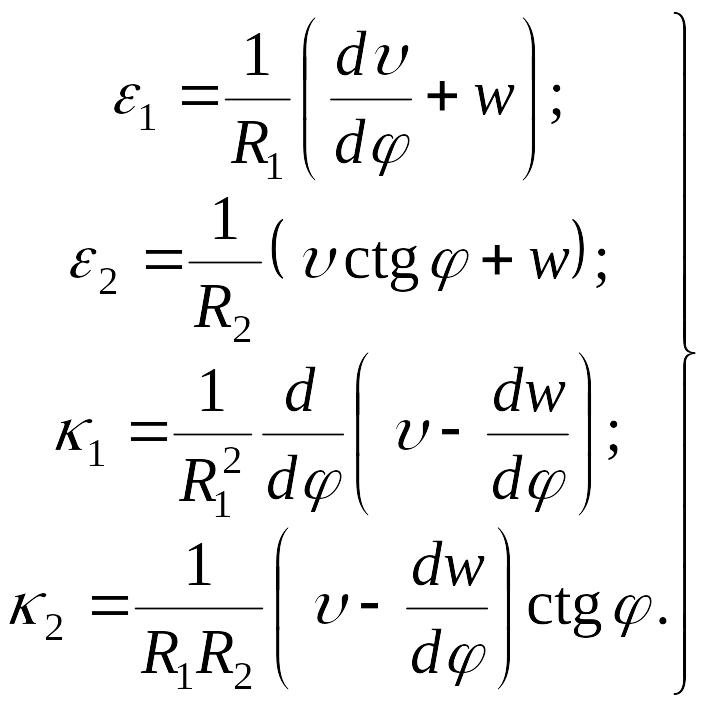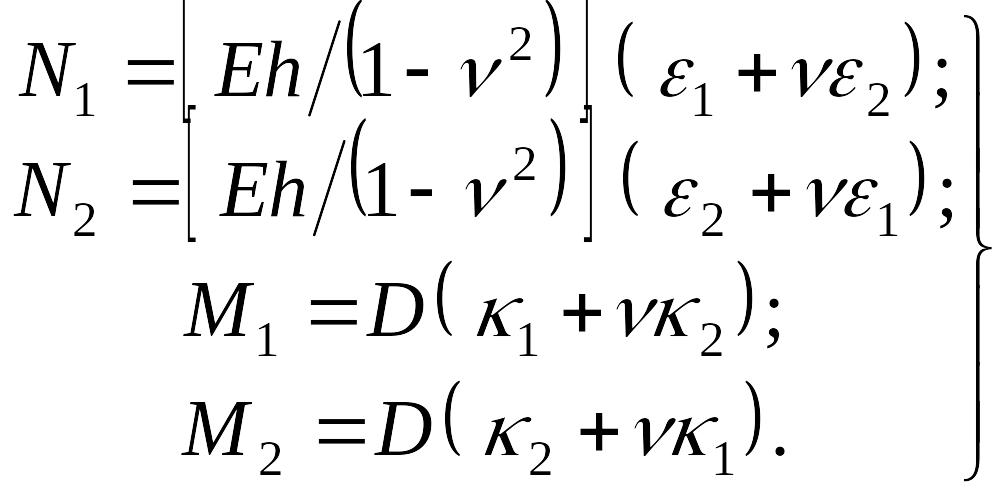7.10 Расчет оболочек вращения на симметричную нагрузку по моментной теории.

Рассмотрим равновесие элемента abcd, вырезанного из оболочки вращения двумя смежными меридиональными плоскостями и двумя сечениями, перпендикулярными меридианам (рис. 7.19).

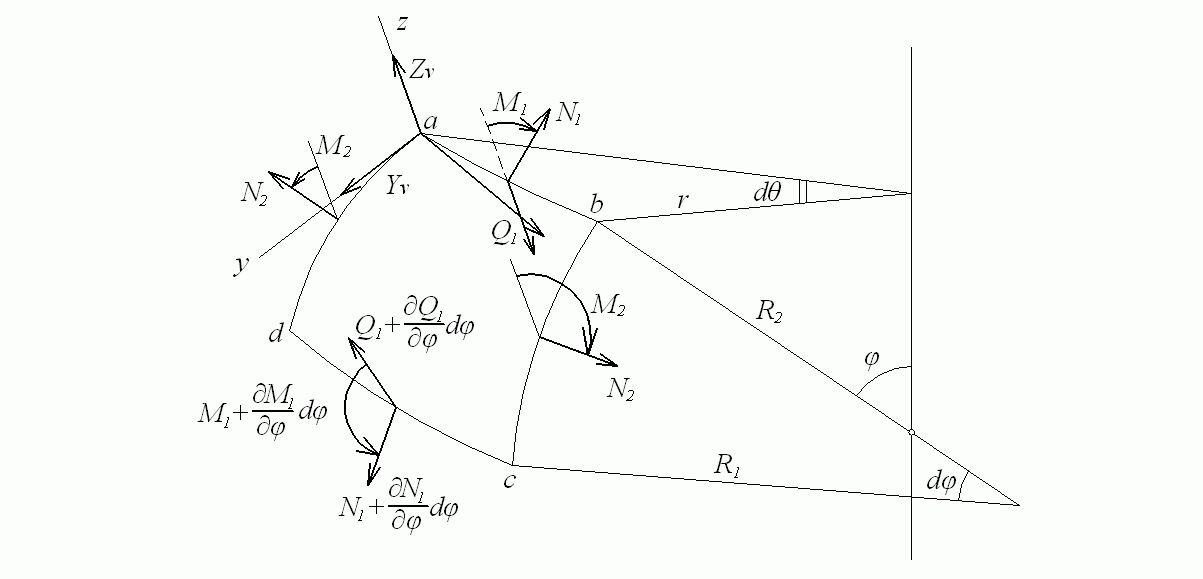
Рис. 7.19. Равновесие элемента оболочки

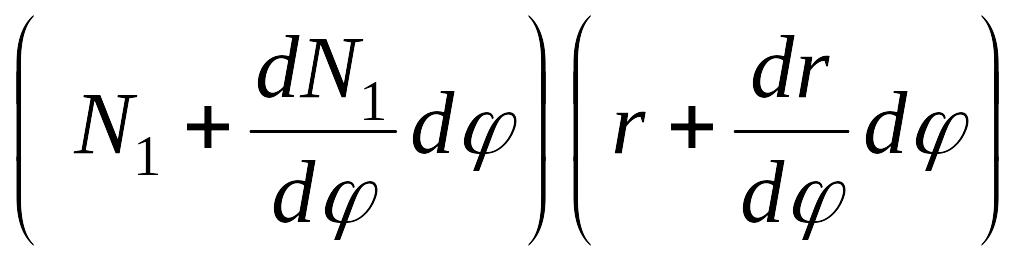Ввиду осевой симметрии на сторонах элемента, расположенных в меридиональных плоскостях, действуют только нормальные силы и изгибающие моменты , независящие от угла . На стороне ab действуют нормальная сила, изгибающий момент и поперечная сила , а на стороне cd — нормальная сила , изгибающий момент 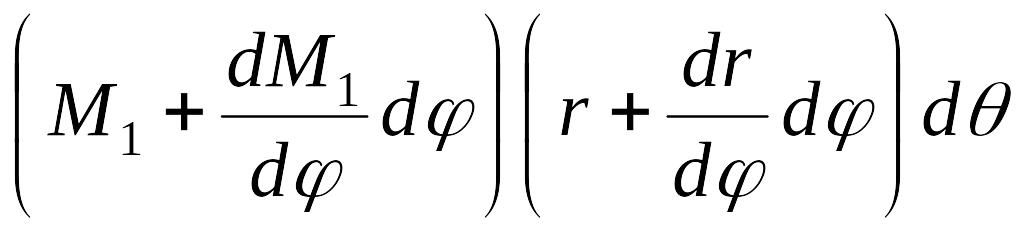и поперечная сила 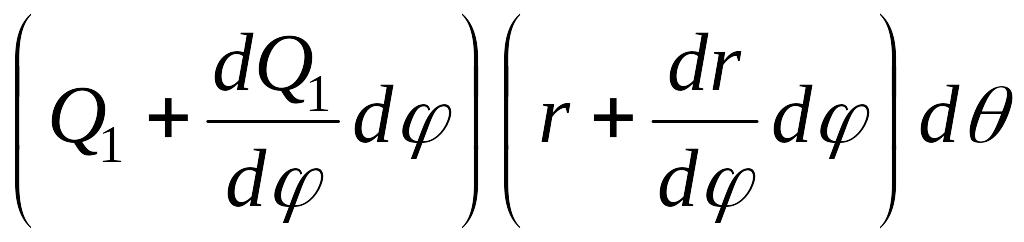. Составляющих поверхностной нагрузки благодаря симметрии будет две: касательная к меридиану и нормальная к срединной поверхности оболочки .

Сумка проекций всех сил, приложенных к рассматриваемому элементу:

на ось y

(а)

на ось z

(б)

Сумма моментов всех сил относительно оси x

(в)

После упрощения уравнений (а), (б) и (в) получаем следующие уравнения равновесия:

(7.28)

В эти три уравнения входят пять неизвестных усилий: , , , и . Следовательно, задача статически неопределима и для решения необходимо рассмотреть еще уравнения деформаций.

В случае симметричной деформации оболочки вращения в каждой точке возникнут только две составляющие перемещения: — перемещение по направлению касательной к меридиану (тангенциальное перемещение) и — перемещение по направлению нормали к срединной поверхности оболочки (радиальное перемещение).

Рассмотрим деформацию элемента AB меридиана (рис. 7.20).

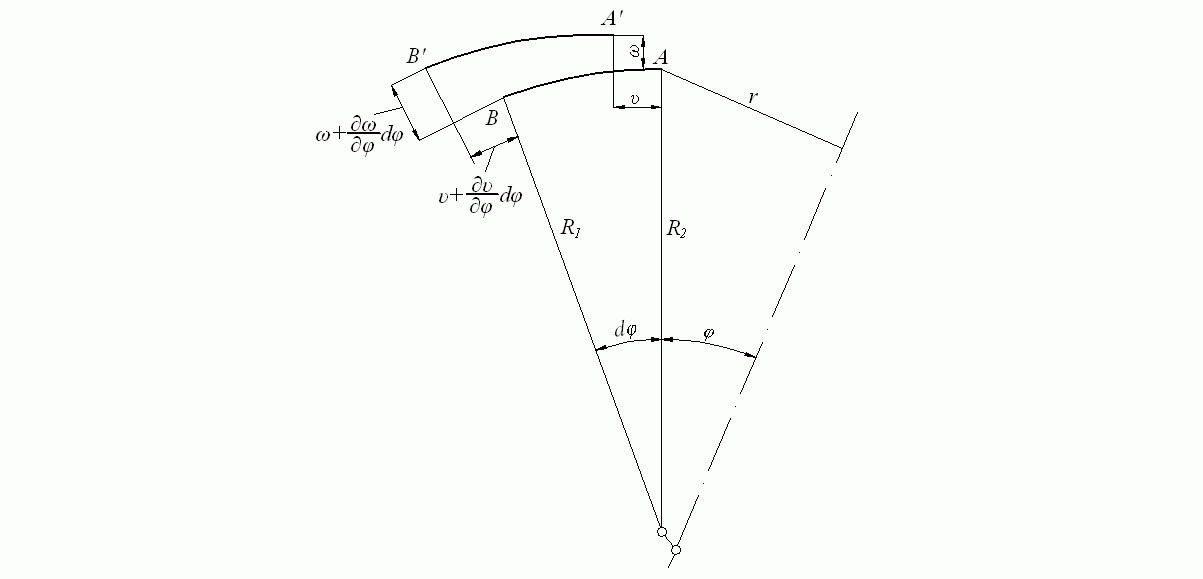
Рис. 7.20. Деформация элемента меридиана оболочки

Удлинение вследствие тангенциальных перемещений точек A и B равно 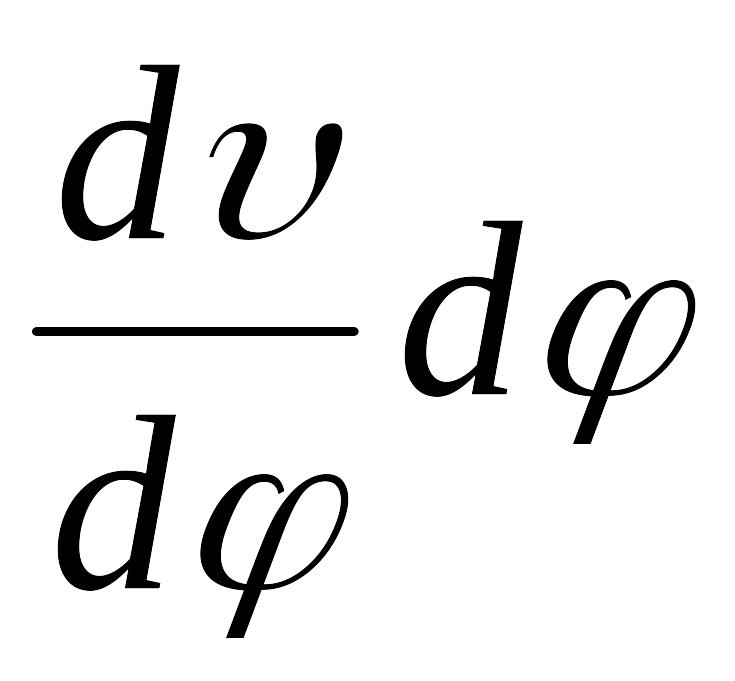, а вследствие радиальных — .

Полное удлинение элемента AB равно сумме . Разделив эту сумму на первоначальную длину элемента, находим линейную деформацию оболочки в меридиональном направлении:

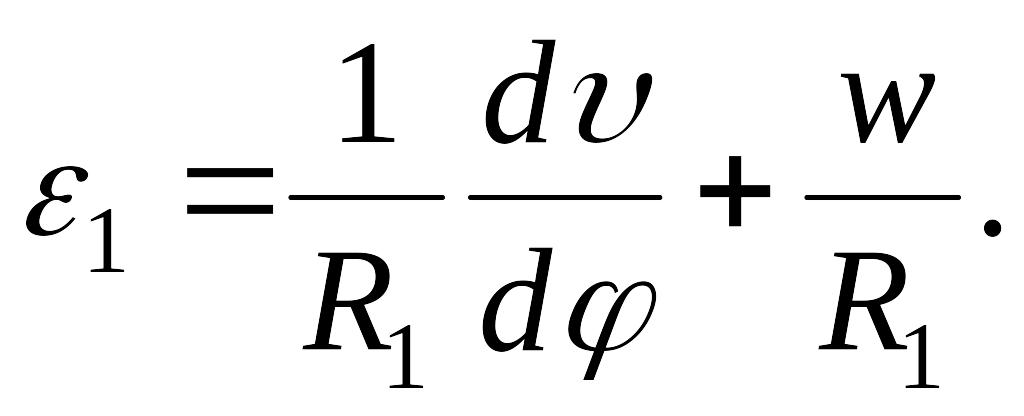
Вследствие перемещений и w радиус r параллельного круга возрастает на величину . Длина окружности параллельного круга возрастает в том же отношении, что и радиус. Поэтому линейная деформация в кольцевом направлении

или после подстановки

Кроме линейных деформаций происходит изменение кривизны оболочки. Вследствие перемещений сторона ab элемента (рис. 7.19) поворачивается относительно оси x на угол

(7.29)

Угол поворота стороны cd будет отличаться на бесконечно малую величину:

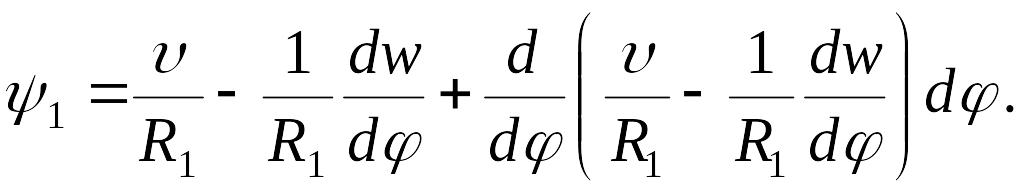
Разделив разность углов поворота этих сторон на первоначальную длину дуги bc, найдем изменение кривизны меридиана:

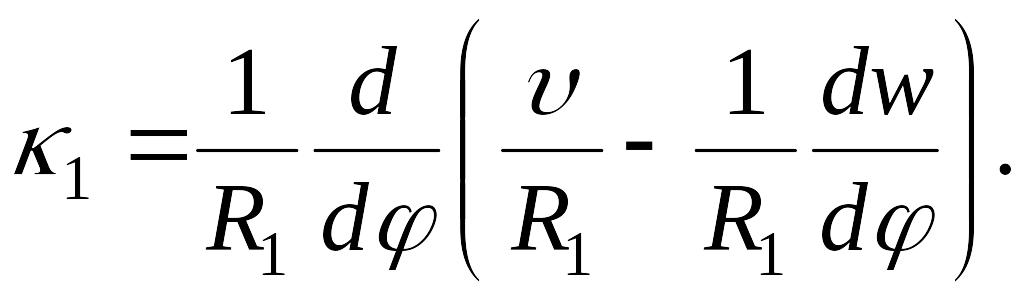
Каждая из боковых сторон элемента abcd благодаря симметрии повернется в меридиональной плоскости на угол . При этом угол их поворота относительно оси y составит

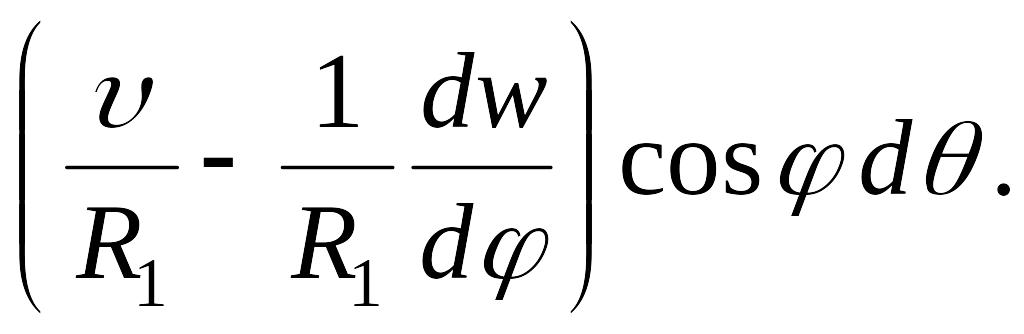
а изменение кривизны в плоскости, перпендикулярной меридиану, будет равно

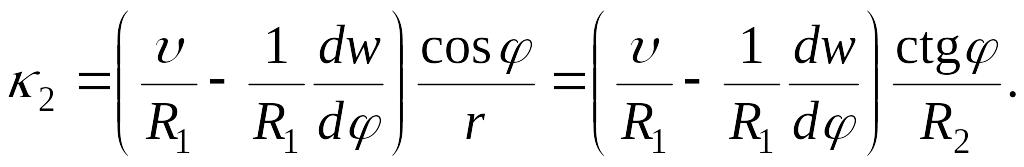
Таким образом, получаем четыре формулы, дающие связь между деформациями и перемещениями в оболочке вращения, находящейся под действием нагрузки, симметричной относительно оси:

(7.30)

Чтобы установить связь между усилиями и деформациями, воспользуемся упрощенными физическими уравнениями теории тонких оболочек (7.11), которые в данном случае будут иметь вид

(7.31)

Формулы (7.28), (7.30) и (7.31) представляют собой систему уравнений с 11 неизвестными: , , , , , , , , , , w. Подставляя формулы (7.31) и (7.30) в уравнение (7.28), можно получить систему трех уравнений с тремя неизвестными: , w, .