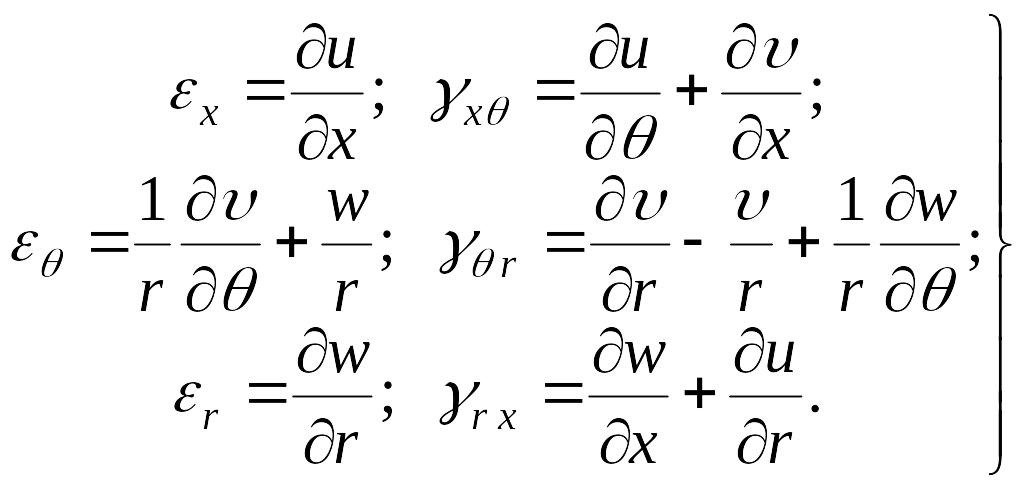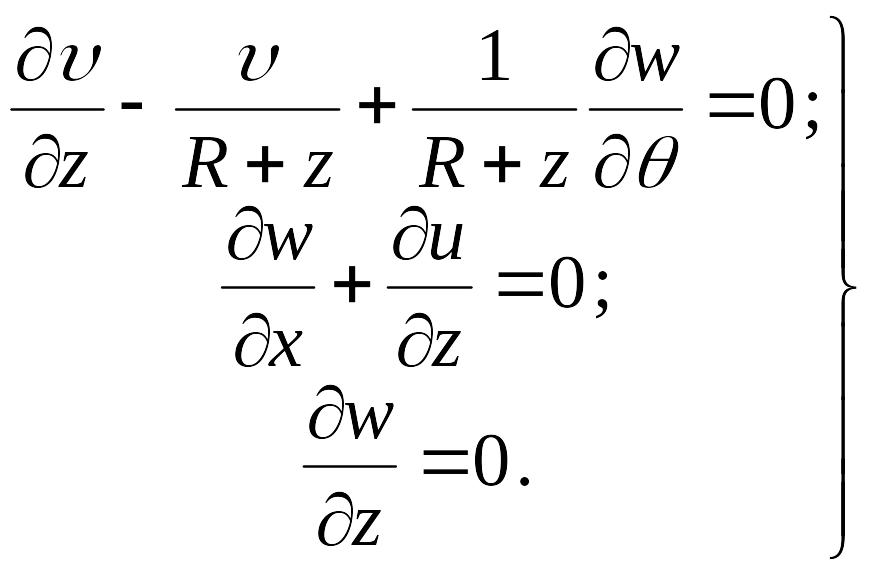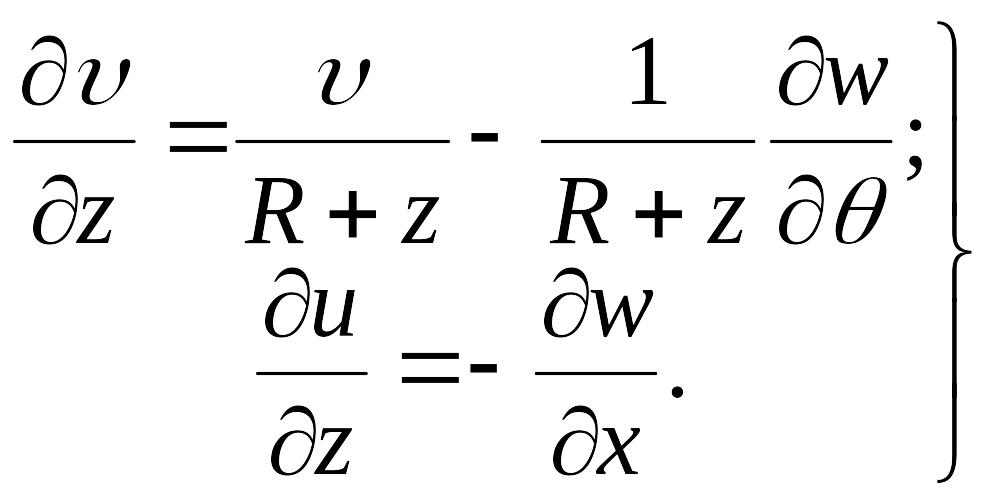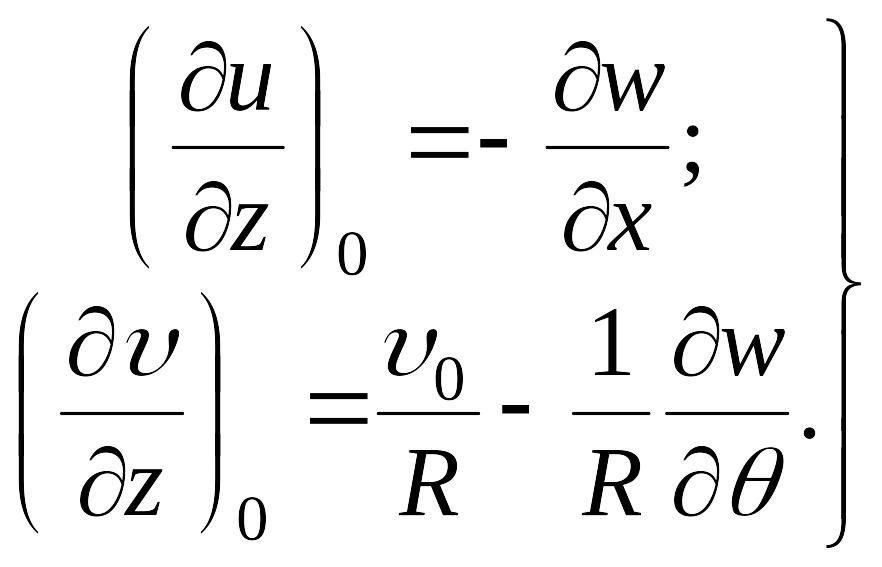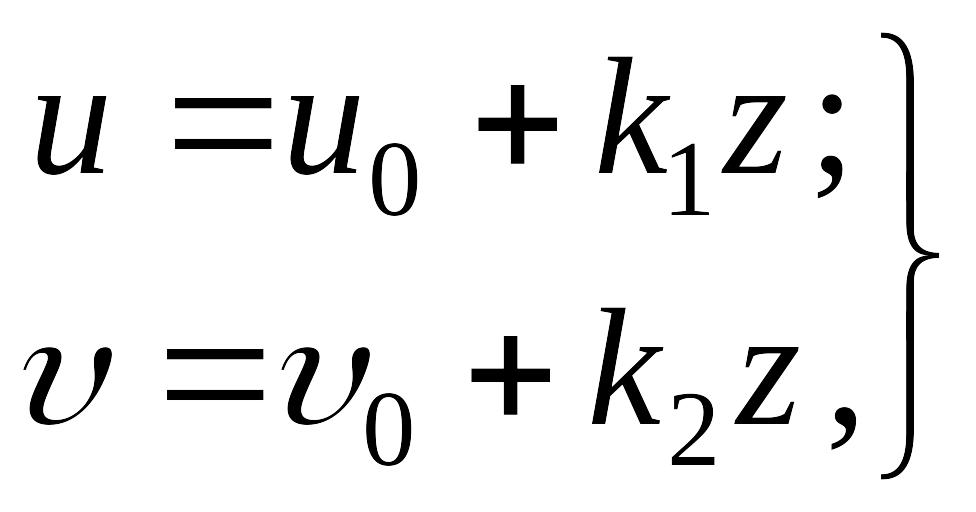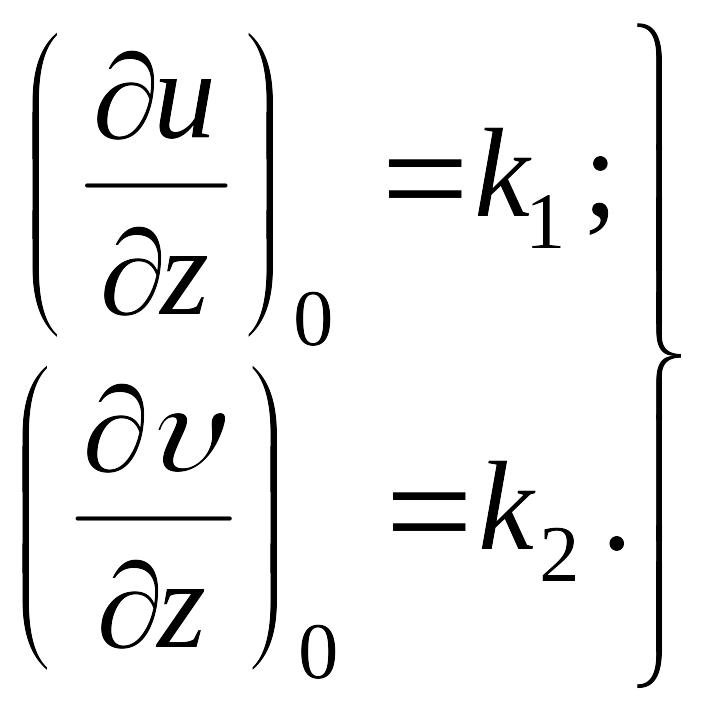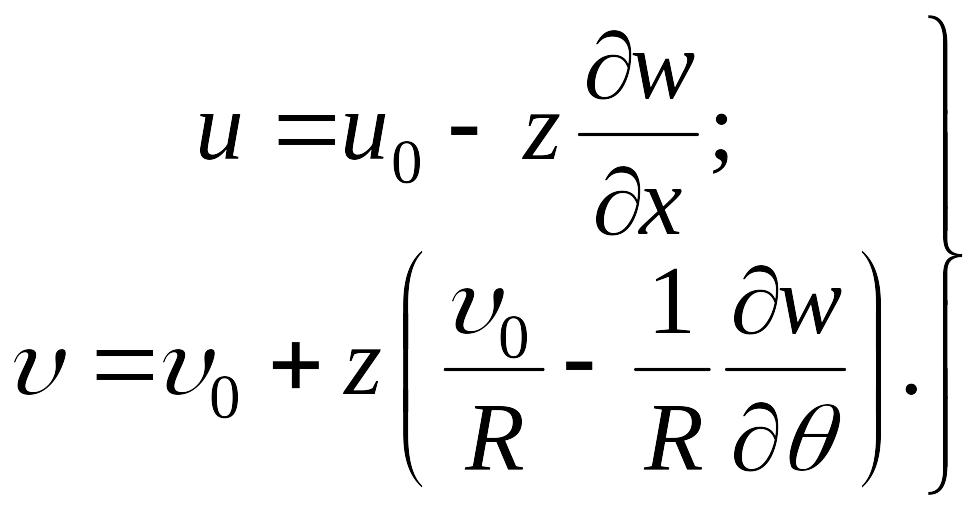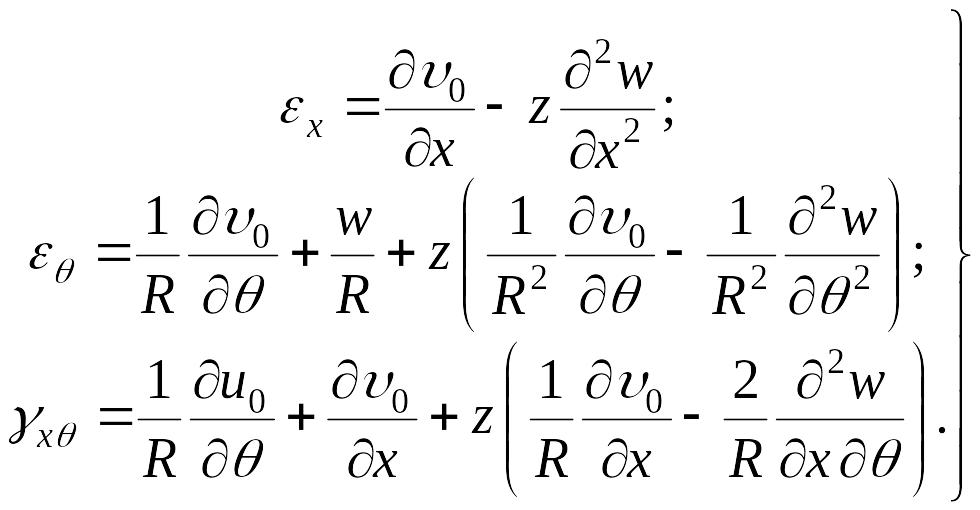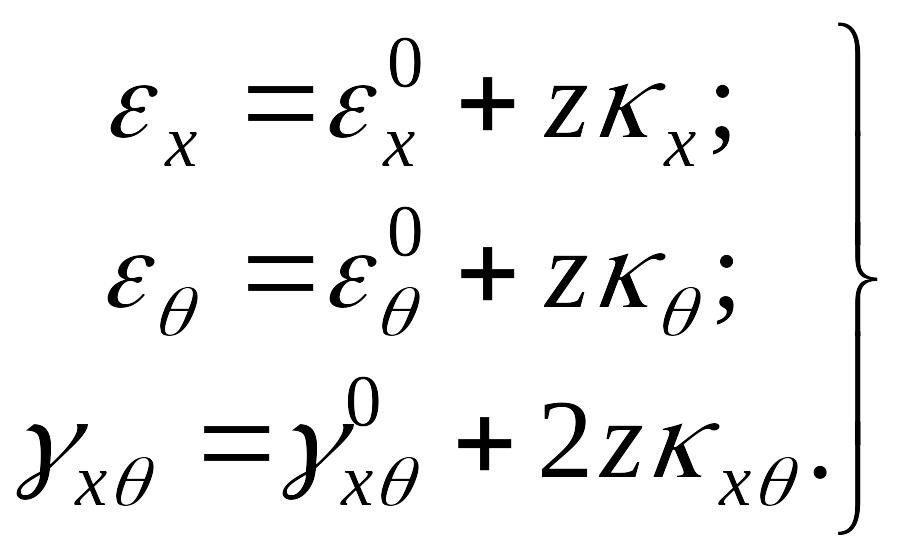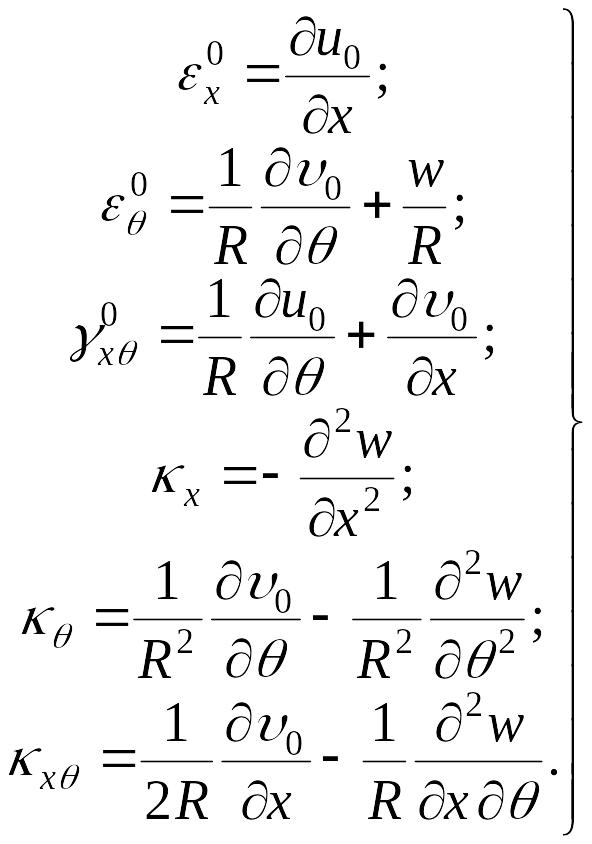7.4 Перемещения и деформации в круговой цилиндрической оболочке

Связь между перемещениями и деформациями в круговой цилиндрической оболочке можно получить из геометрических соотношений Коши в цилиндрической системе координат x, , r (рис. 7.13).

Составляющие перемещения в этой системе имеют следующий смысл: u — составляющая вдоль оси x; — составляющая в направлении оси , т. е. перпендикулярная в каждой точке плоскости xOr; — составляющая в направлении оси r.

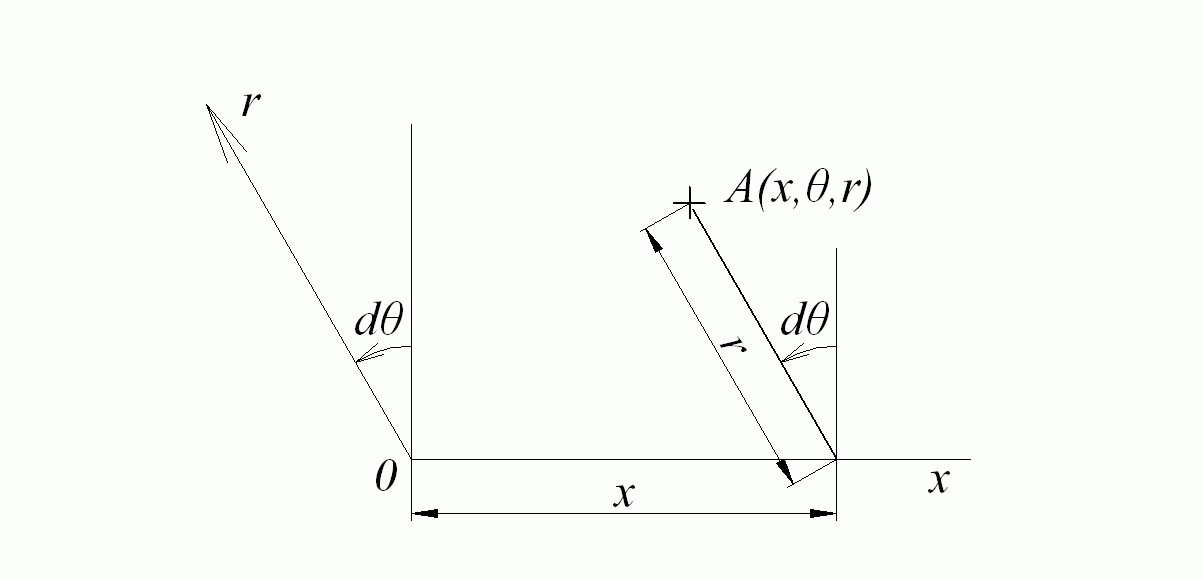
Рис. 7.13. Цилиндрическая система координат

Составляющие линейной деформации в цилиндрической системе координат x, , r будем обозначать , и , а составляющие угловой деформации — , , . Уравнения Коши в цилиндрической системе координат (без вывода):

(7.6)

Для перехода от пространственного тела к оболочке вместо цилиндрической системы координат x, , r введем систему координат x, , z, связанную со срединной поверхностью оболочки. При этом координаты x и сохранят свое значение, а координата r преобразуется к координате z:

(а)

где R — радиус срединной поверхности; здесь — величина постоянная.

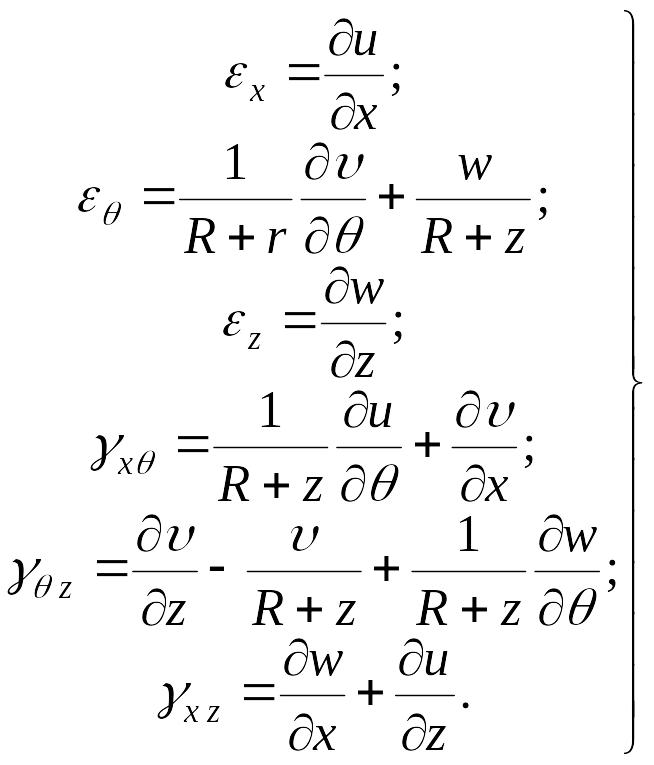
Переход от одной системы координат к другой в выражениях производных сводится к простой замене переменной r на z. Таким образом, геометрические соотношения Коши в системе координат x, , z примут вид:

(б)

Из гипотезы прямых нормалей следует, что

(7.7)

Подставляя в эти условия выражения составляющих деформации из соотношений (б), получаем

(в)

Третья строка формул (в) указывает на то, что перемещение по нормали к срединной поверхности оболочки не зависит от координаты z, т. е. w=w(x, y), и все точки, лежащие на нормали, получают одинаковые перемещения в направлении этой нормали, равные перемещению точки срединной поверхности.

Из двух первых формул (в) получаем

(г)

Производные и в точках срединной поверхности оболочки, т. е. при , принимают следующие значения:

(д)

Здесь, как и в дальнейшем, индекс 0 относится к значениям функций в точках срединной поверхности оболочки.

На основании гипотезы прямых нормалей составляющие перемещения u и должны быть линейными функциями относительно координаты z, т. е. их можно представить в такой форме:

(е)

где k₁ и k₂ — угловые коэффициенты нормали к срединной поверхности соответственно в координатных плоскостях zCx и . Они являются функциями координат x и . Для определения угловых коэффициентов продифференцируем формулы (е) по z и, подставив , найдем значения этих производных на срединной поверхности:

(ж)

Сравнивая (д) и (ж), получаем значения угловых коэффициентов:

Подставляя эти значения в формулы (е), находим составляющие перемещения u и , являющиеся решениями уравнений в частных производных (г):

(з)

Таким образом, составляющие перемещения произвольной точки оболочки выражены через составляющие перемещения точки ее срединной поверхности u₀ , ₀ и . Подставляя соотношения (з) в формулы (б) и пренебрегая при этом величиной z ввиду ее малости по сравнению с R, находим

(7.8)

Это – геометрические уравнения теории круговой цилиндрической оболочки. Они устанавливают связь между деформациями в произвольной точке оболочки и перемещениями соответствующей точки срединной поверхности. Эти уравнения удобно представить в таком виде:

(7.9)

Первые слагаемые в этих формулах представляют собой деформации точек срединной поверхности, а вторые связаны с изгибом и кручением срединной поверхности, а именно: k_x – кривизна оболочки в направлении оси x после деформирования; k_θ – изменение кривизны в направлении дуги; k_xθ – относительное кручение срединной поверхности оболочки.

Из сопоставления формул (7.8) и (7.9) получаем

(7.10)