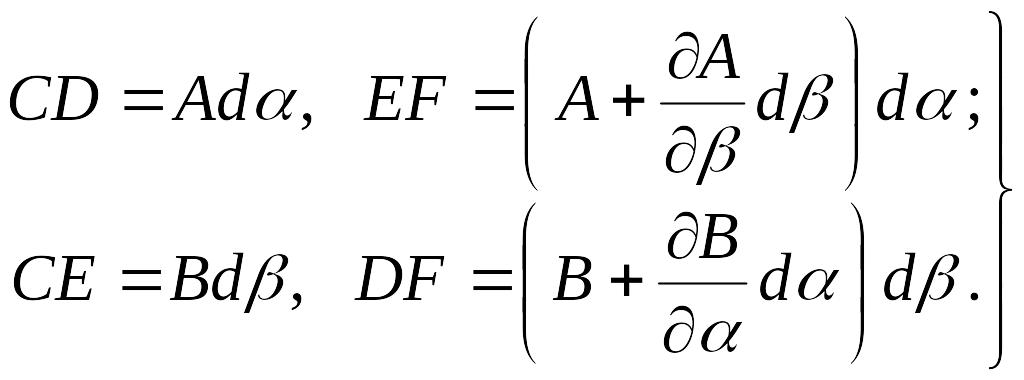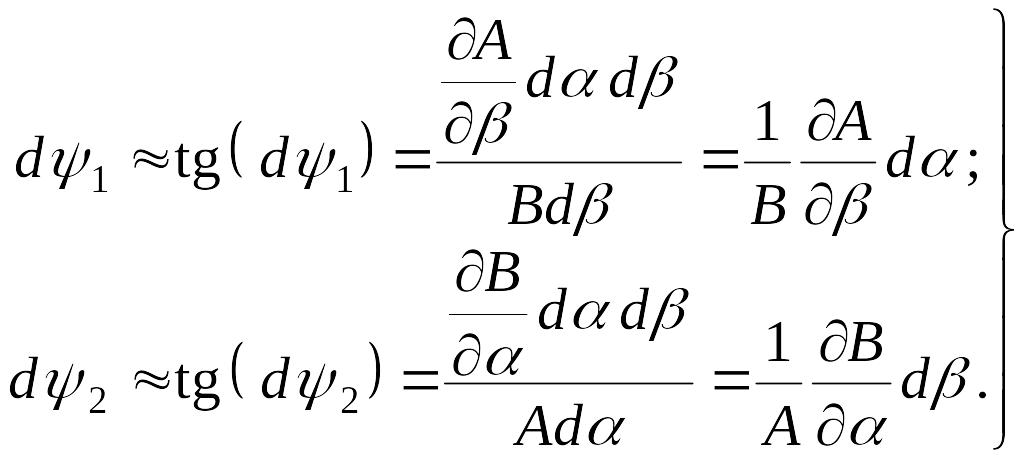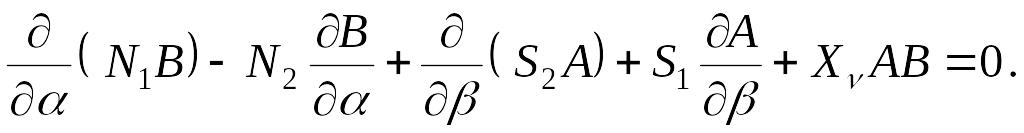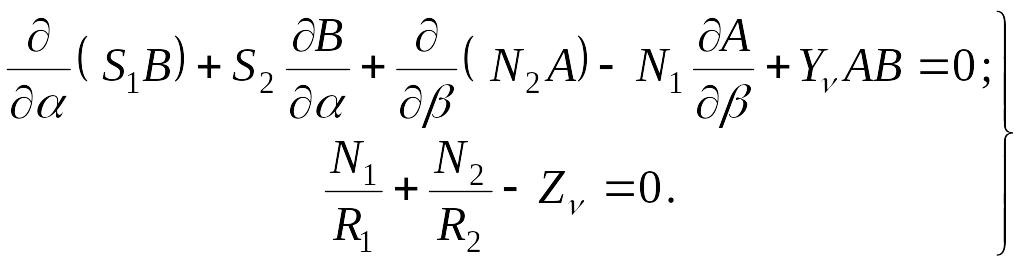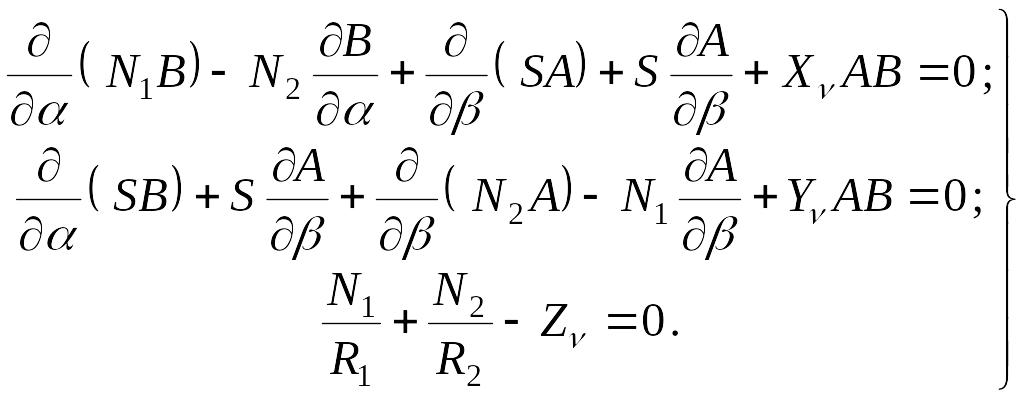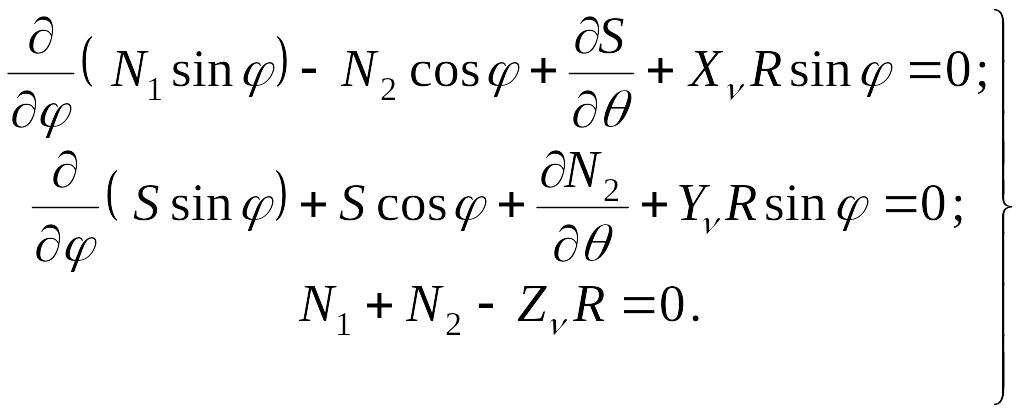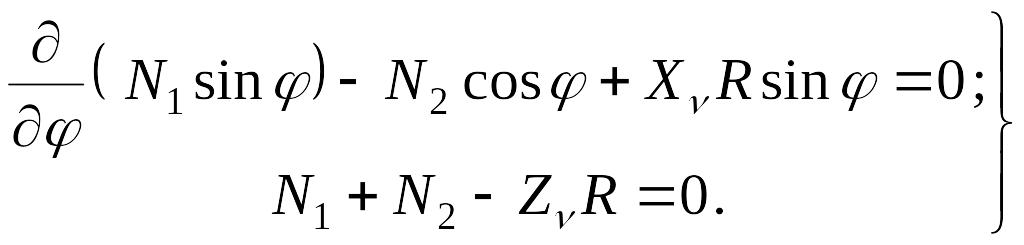53

Спец. Разделы. Лекции. Расчет оболочки произвольной формы по моментной теории

Для оболочки произвольной формы применяют криволинейные ортогональные координаты α и β (рис. 7.4). Бесконечно малые дуги ds₁ и ds₂ на криволинейной поверхности можно рассматривать как прямые. В теории поверхностей их называют линейными элементами. Длины линейных элементов пропорциональны дифференциалам независимых переменных:

(а)

Коэффициенты пропорциональности A и B преобразуют приращения криволинейных координат в линейные отрезки. В общем случае эти коэффициенты являются функциями координат α и β.

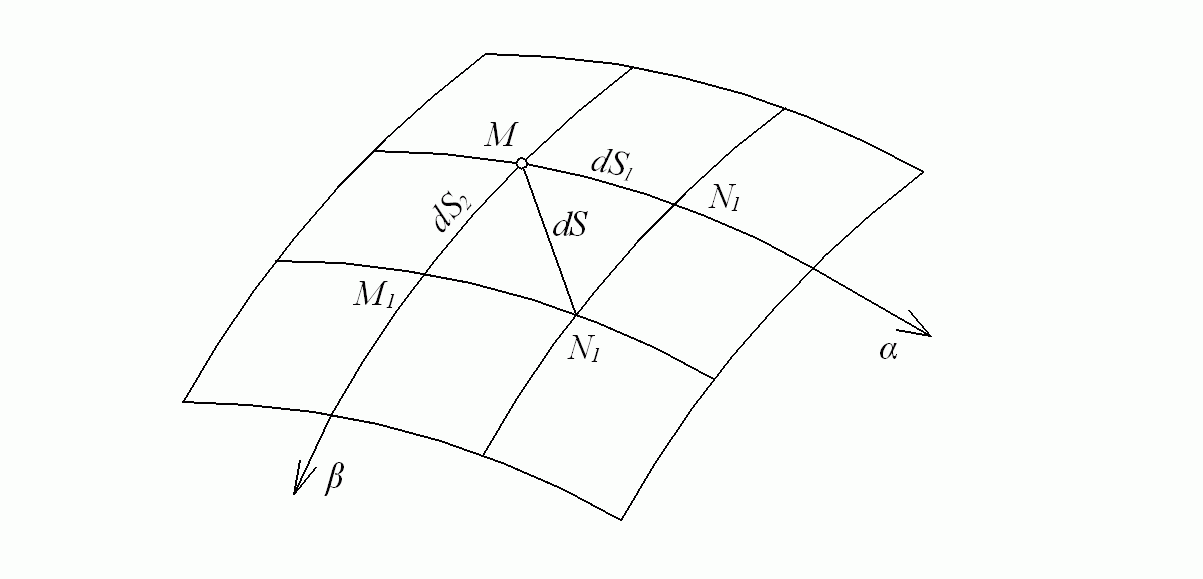
Рис. 7.4. Система криволинейных координат

Квадрат линейного элемента в ортогональных координатах составляет

или с учетом зависимостей (а)

(б)

Выражение (б) называется первой квадратичной формой поверхности, а величины A и B — коэффициентами первой квадратичной формы.

Для исследования внутренних усилий выделим из срединной поверхности оболочки линиями , , и бесконечно малый элемент CDFE (рис. 7.5). В координатах α и β он имеет форму ортогонального криволинейного четырехугольника со сторонами

(в)

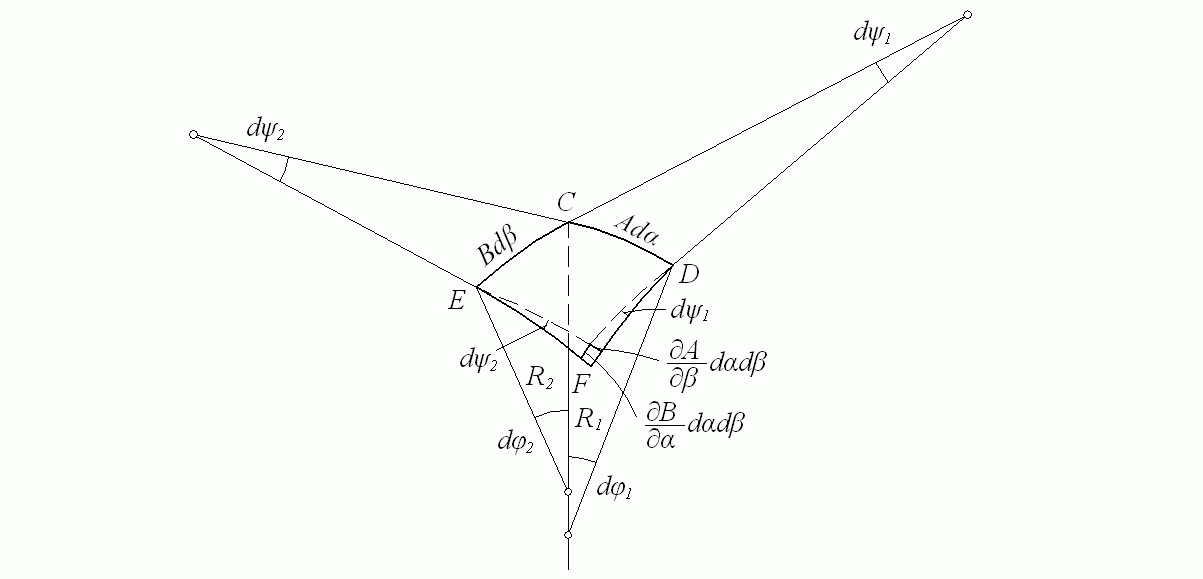
Рис. 7.5. К исследованию внутренних усилий

Углы dφ₁ и dφ₂, соответствующие сторонам четырехугольника Adα и Bdβ, расположены в двух взаимно перпендикулярных главных нормальных плоскостях, проходящих через точку C. Согласно рисунку, эти углы определяются формулами

(г)

Углы dψ₁ и dψ₂ лежат в касательной плоскости и образованы направлениями смежных касательных к линиям кривизн, проходящих через точки C, D и E. Для этих углов получаем

(д)

В случае безмоментного напряженного состояния на гранях рассматриваемого элемента действуют отнесенные к единице длины сечения оболочки нормальные N₁, N₂ и сдвигающие S₁, S₂ усилия, являющиеся функциями координат α и β. Эти усилия изображены на рис. 7.6.

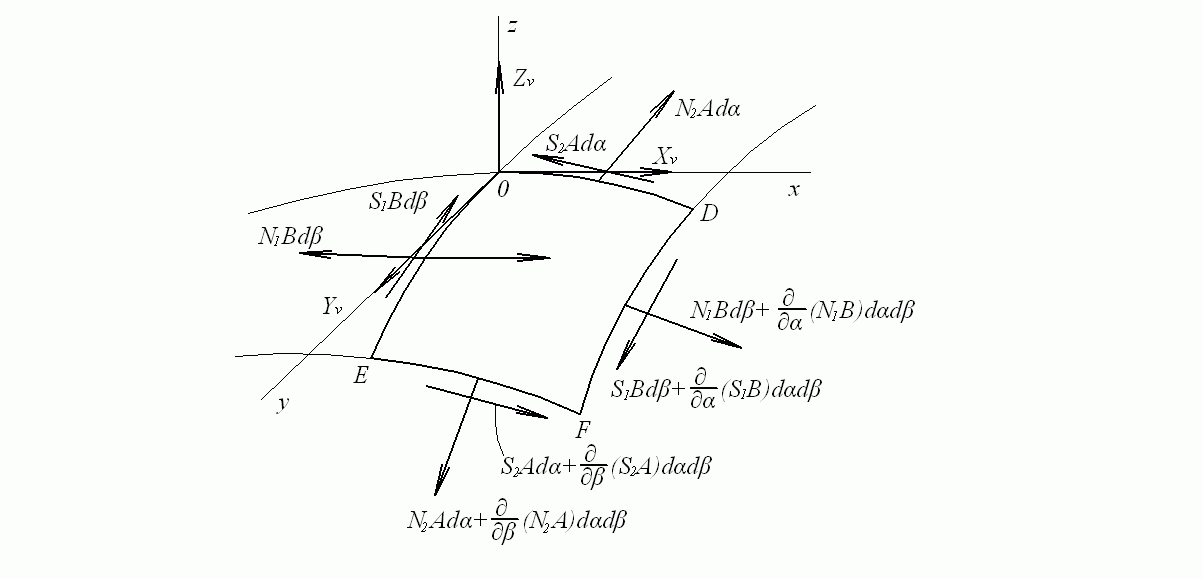
Рис. 7.6. Нормальные и сдвигающие усилия

Поверхностная нагрузка показана в виде составляющих интенсивности нагрузки X_ν, Y_ν, Z_ν по осям подвижной ортогональной системы координат xyz с началом в точке С.

Рассмотрим условия равновесия элемента CDFE. Сумма проекций всех сил на ось Cx

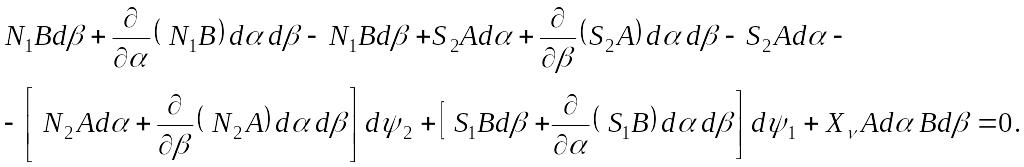
Приведем подобные члены и отбросим стоящие в квадратных скобках величины высшего порядка малости:

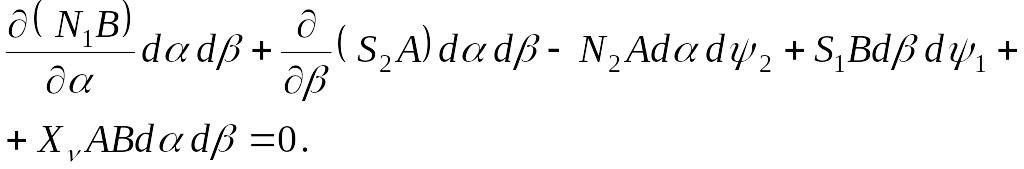
Отсюда после подстановки значений углов (д) и упрощения находим

(е)

Аналогично получаем еще два уравнения равновесия, проецируя все силы на оси и :

(ж)

Из уравнения моментов относительно оси Cz получаем соотношение

называемое законом парности сдвигающих усилий. С его учетом дифференциальные уравнения равновесия безмоментной теории оболочек можно представить в таком виде:

(7.1)

Уравнения (7.1) представляют собой полную систему основных уравнений безмоментной теории оболочек, выведенную в линиях главных кривизн срединной поверхности оболочки. Число неизвестных функций N₁, N₂ и S₁ соответствует числу уравнений, т. е. при расчете по безмоментной теории оболочка в бесконечно малом представляет собой статически определимую систему.

Решение системы уравнений (7.1) относится к статической задаче безмоментной теории оболочек. Чтобы найти деформации и перемещения в оболочке, к этим уравнениям следует добавить геометрические и физические уравнения. Здесь ограничиваемся исследованием только статической стороны задачи и рассмотрим основные уравнения для двух частных случаев.

Сферическая оболочка. В этом случае главные радиусы кривизны одинаковы:

Заменяя координату на , а на , согласно рис. 7.7 получаем следующие значения длин линейных элементов:

(з)

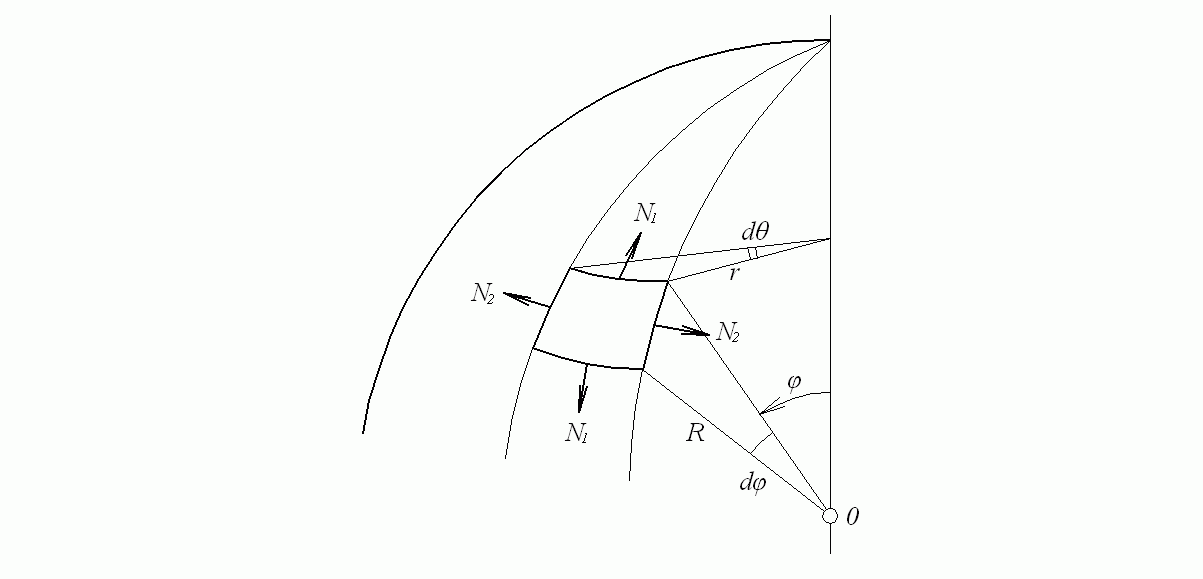
Рис. 7.7. Преобразование координат в сферической оболочке

Сравнивая соотношения (з) и (а), заключаем, что коэффициенты первой квадратичной формы принимают вид

и уравнения (7.1) преобразуются в следующие:

(7.2)

Осесимметричное нагружение сферической оболочки. В этом случае усилия не зависят от угла и все производные по обращаются в нуль. Кроме того, сдвигающие усилия . Действительно, в силу симметрии в любом меридиональном сечении слева и справа должны существовать одинаковые сдвигающие усилия, направленные в одну сторону. Это противоречит условиям равновесия и возможно лишь при . Из уравнений (7.2) остаются только два:

(7.3)

В связи с определенностью направлений главных кривизн усилия в сферической оболочке имеют следующие названия: N₁ – меридиональное усилие (направление совпадает с направлением меридианов на сфере), N₂ – кольцевое усилие.

Рассмотрим решение системы уравнений (7.3) на примере сферического купола, к которому приложена равномерно распределенная нагрузка интенсивностью q на единицу площади горизонтальной проекции оболочки (рис. 7.8). Согласно этому рисунку, составляющие поверхностной нагрузки таковы:

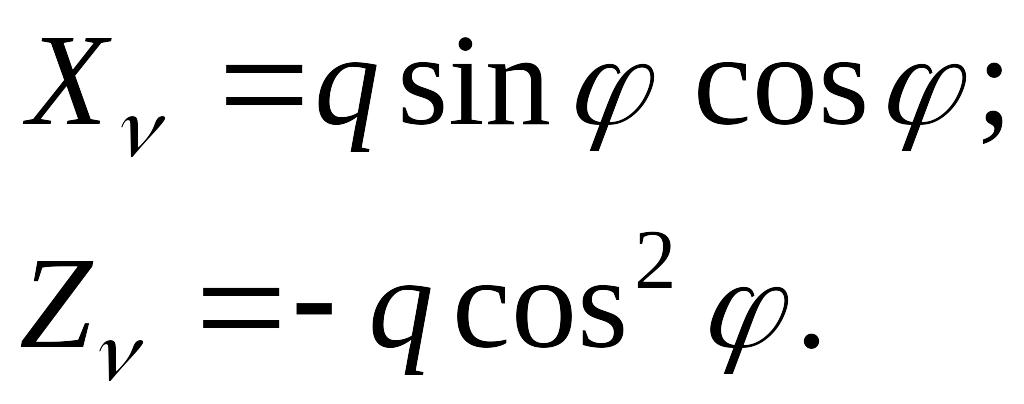
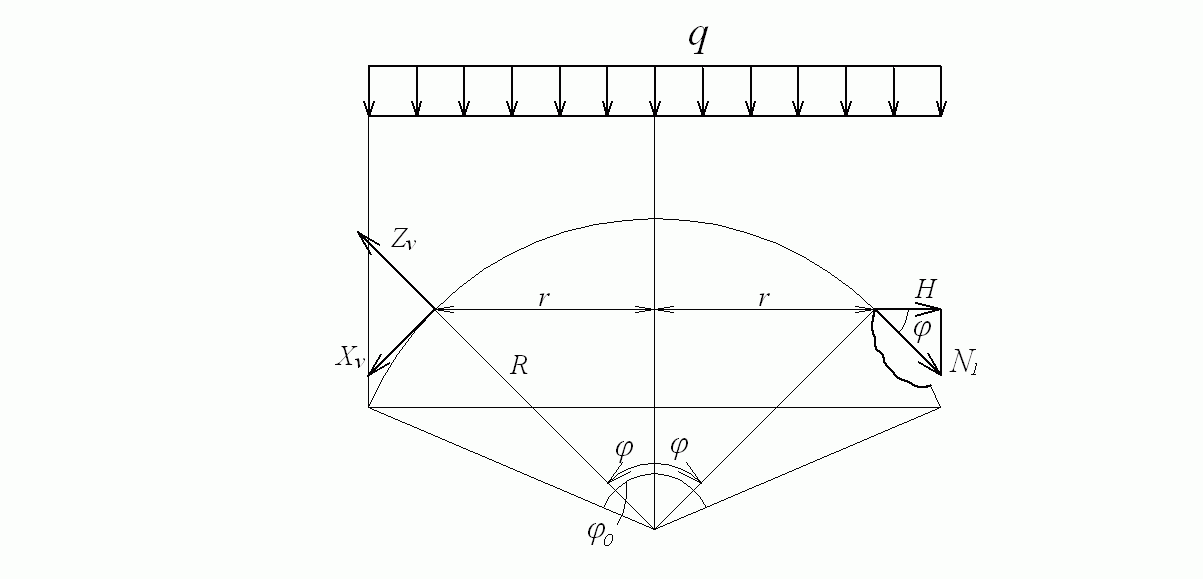
Рис. 7.8. Сферический купол

Подставляя их значения в уравнения (7.3), получаем:

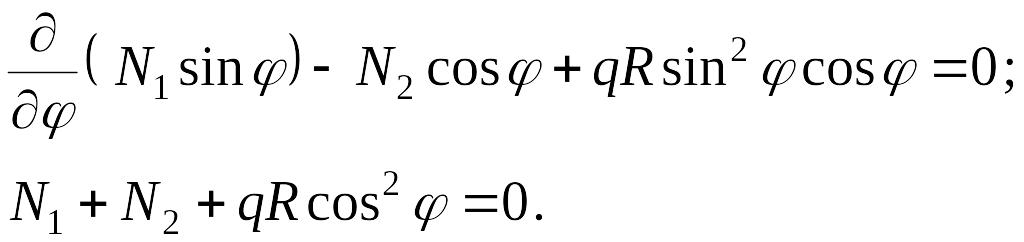
Решение этой системы уравнений дает

Эпюры меридиональных и кольцевых усилий по высоте купола изображены на рис. 7.8.

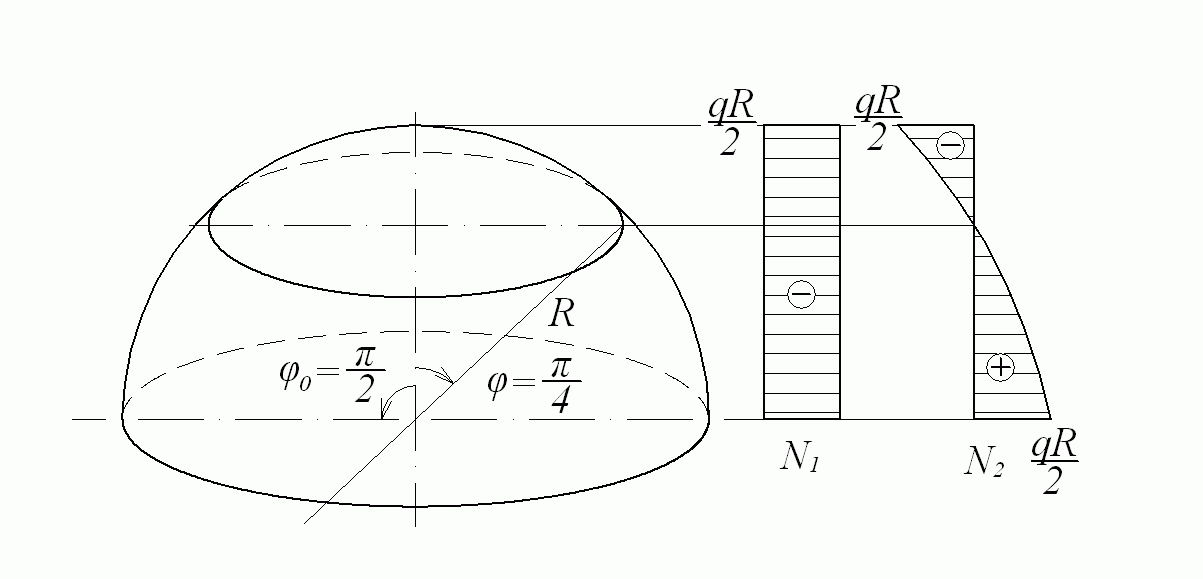
Рис. 7.8. Эпюры меридиональных и кольцевых усилий

Сжимающее кольцевое усилие имеет максимальное абсолютное значение в вершине купола при φ = 0. По мере продвижения вниз кольцевое усилие уменьшается и при φ = 45º равно нулю. Далее оно становится растягивающим и возрастает. Меридиональное усилие остается постоянно сжимающим.

Для определения горизонтальной составляющей меридионального усилия рассмотрим рис. 7.7, откуда

На нижнем краю купола при возникает горизонтальная составляющая реакции

(и)

для восприятия которой купол ставят на опорное кольцо. Реакция создает в кольце растягивающие усилия. Значение этих усилий определим из рассмотрения равновесия половины опорного кольца (рис. 7.9).

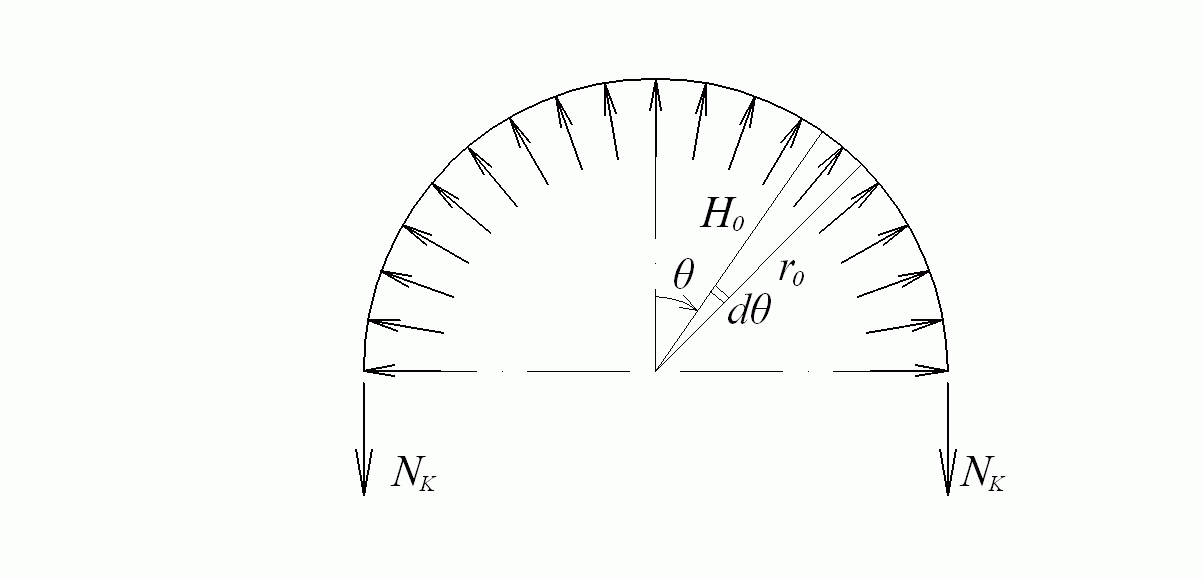
Рис. 7.9. Равновесие половины опорного кольца

Проецируя все силы на вертикальную ось, получаем

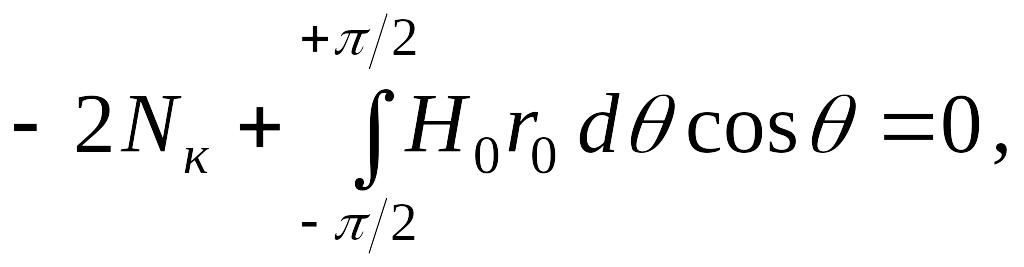
откуда после интегрирования искомое усилие

или с учетом формул (з) и (и)

Наибольшего значения растягивающее усилие в опорном кольце достигает при угле φ₀ = 45º. При φ₀ = 90º усилие становится равным нулю и необходимость в опорном кольце отпадает.