- •Предмет и метод статистики
- •4Понятие и виды группировок.Принципы построения группировок.Количественные и атрибутивные признаки. Групприровочный признак.Интервальные группировки.
- •5.Понятие статистического показателя.Абсолютные,относительные и среднии показатели.Средняя арифметическая,гармоническая,геометрическая,квадратическая простая и взвешенная.
- •7)Понятие рядов распределения. Дискретные и интервальные ряды распределения
- •1.1. Атрибутивные ряды распределения
- •1.2. Вариационные ряды распределения
- •8. Показатели вариации и способы их расчета. Виды дисперсии в совокупности, распределенной на части. Правило сложения дисперсии.
- •9. Моменты распределения. Показатели формы распределения.
- •13. Понятие доверительного интервала для среднего и доли генеральной совокупности и его определение по показателям выборки.
- •14. Понятие доверительного интервала для среднего и доли генеральной совокупности и его определение по показателям выборки
- •15. Понятие корреляционной зависимости. Поле корреляции. Методы выявления корреляционных связей. Коэффициент Фехнера.
- •17. Понятие ранга. Коэффициент ранговой корреляции Спирмена.
- •18. Уравнение регрессии и его виды. Определение параметров линейного уравнения регрессии. Коэффициент эластичности.
- •2 Типа взаимосвязей между х и у:
- •19. Теоретический коэффициент детерминации и теоретическое корреляционное отношение.
- •20. Оценка значимости коэффициента регрессии и уравнения связи.
- •Вопрос 21. Понятие временного ряда. Виды прогнозов. Общая характеристика методов прогнозирования.
- •Вопрос 22. Аналитические показатели динамики временных рядов.
- •Вопрос 23. Средние показатели динамики временных рядов. Прогнозирование по среднему абсолютному приросту и среднему темпу роста.
- •Вопрос 24. Стационарные временные ряды, проверка ряда на стационарность, построение доверительного интервала для прогноза.
- •Вопрос 25. Выявление основной тенденции в рядах динамики Метод скользящей средней.
- •35. Статистика материальных оборотных средств
- •36.Статистика трудовых ресурсов.
- •26. Определение параметров уравнения тренда. Прогнозирование на основе тренда. Доверительный интервал прогноза.
- •1) Индекс физического объема продукции:
- •2) Индекс цен:
- •3) Индекс себестоимости:
- •29. Индексы Ласпейреса, Пааше и Фишера. Индекс Эджворта и их экономический смысл.
- •30. Индексы фиксированного и переменного состава. Индекс структурных сдвигов. Взаимосвязь индексов и их экономическое содержание.
- •Вопрос 31. Система национальных счетов (снс)
- •Вопрос 32. Макроэкономические показатели и их взаимосвязь. Расчет ввп производственным, распределительным методом и методом конечного использования
- •Вопрос 33. Национальное богатство.
- •Вопрос 34. Статистика основных фондов (оф).
- •35. Статистика материальных оборотных средств
- •36.Статистика трудовых ресурсов.
14. Понятие доверительного интервала для среднего и доли генеральной совокупности и его определение по показателям выборки
Основные
характеристики параметров генеральной
и выборочной совокупностей обозначаются
символами: N
– объем генеральной совокупности
(число входящих в нее единиц); n
– объем выборки (число обследованных
единиц);
 - генеральная средняя (среднее значение
признака в генеральной совокупности);
- генеральная средняя (среднее значение
признака в генеральной совокупности);
 -
выборочная средняя; p
–
генеральная доля (доля единиц, обладающих
данным значением признака в общем числе
единиц генеральной совокупности); w
– выборочная доля. Доля
выборки
есть отношение числа единиц выборочной
совокупности к числу единиц генеральной
совокупности:
-
выборочная средняя; p
–
генеральная доля (доля единиц, обладающих
данным значением признака в общем числе
единиц генеральной совокупности); w
– выборочная доля. Доля
выборки
есть отношение числа единиц выборочной
совокупности к числу единиц генеральной
совокупности:
 .
Обычно используют: среднюю
величину количественного признака и
относительную величину альтернативного
признака
(долю или удельный вес единиц в
статистической совокупности, которые
отличаются наличием изучаемого
признака). Выборочная
доля ( w
)
определяется отношением числа единиц,
обладающих изучаемым признаком т,
к общему числу единиц выборочной
совокупности п:
w
= т / п .
Для характеристики надежности выборочных
показателей различают среднюю
и предельную ошибки выборки. Ошибка
выборки
.
Обычно используют: среднюю
величину количественного признака и
относительную величину альтернативного
признака
(долю или удельный вес единиц в
статистической совокупности, которые
отличаются наличием изучаемого
признака). Выборочная
доля ( w
)
определяется отношением числа единиц,
обладающих изучаемым признаком т,
к общему числу единиц выборочной
совокупности п:
w
= т / п .
Для характеристики надежности выборочных
показателей различают среднюю
и предельную ошибки выборки. Ошибка
выборки
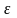 или, иначе говоря, ошибка репрезентативности
- разность соответствующих выборочных
и генеральных характеристик: для
средней количественного признака
или, иначе говоря, ошибка репрезентативности
- разность соответствующих выборочных
и генеральных характеристик: для
средней количественного признака
 ;
для
доли (альтернативного признака)
;
для
доли (альтернативного признака)
 .
Выборочная средняя и выборочная доля
- случайные величины принимающие
различные значения в зависимости от
того, какие единицы совокупности попали
в выборку. Поэтому определяют среднюю
из возможных ошибок – среднюю ошибку
выборки. Средняя
ошибка выборки при повторном отборе
рассчитывается по следующим формулам:
для
средней количественного признака:
.
Выборочная средняя и выборочная доля
- случайные величины принимающие
различные значения в зависимости от
того, какие единицы совокупности попали
в выборку. Поэтому определяют среднюю
из возможных ошибок – среднюю ошибку
выборки. Средняя
ошибка выборки при повторном отборе
рассчитывается по следующим формулам:
для
средней количественного признака:
 ;
для
доли (альтернативного признака):
;
для
доли (альтернативного признака):
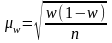 .
Средняя
ошибка выборки при бесповторном отборе
рассчитывается по следующим формулам:
для
средней качественного признака
.
Средняя
ошибка выборки при бесповторном отборе
рассчитывается по следующим формулам:
для
средней качественного признака
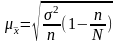 ;
для
доли (альтернативного признака)
;
для
доли (альтернативного признака)
 .
В каждой конкретной выборке расхождение
между выборочной средней и генеральной
.
В каждой конкретной выборке расхождение
между выборочной средней и генеральной
 может
быть меньше средней ошибки
может
быть меньше средней ошибки
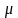 ,
равно ей или больше ее. Каждое из этих
расхождений имеет различную вероятность.
Поэтому фактические расхождения между
выборочной средней и генеральной
рассматривают как предельную
ошибку,
связанную со средней ошибкой и
гарантируемую с определенной вероятностью
Р.
Предельную
ошибку выборки
можно рассчитать по следующим формулам:
при
повторном отборе:
для средней
,
равно ей или больше ее. Каждое из этих
расхождений имеет различную вероятность.
Поэтому фактические расхождения между
выборочной средней и генеральной
рассматривают как предельную
ошибку,
связанную со средней ошибкой и
гарантируемую с определенной вероятностью
Р.
Предельную
ошибку выборки
можно рассчитать по следующим формулам:
при
повторном отборе:
для средней
 ,
где t
– нормированное отклонение – «коэффициент
доверия», зависящий от вероятности, с
которой гарантируется предельная
ошибка выборки;
,
где t
– нормированное отклонение – «коэффициент
доверия», зависящий от вероятности, с
которой гарантируется предельная
ошибка выборки;
 -
средняя ошибка выборки; для
доли
-
средняя ошибка выборки; для
доли
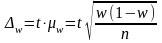 ;
при бесповторном отборе: для
средней
;
при бесповторном отборе: для
средней
 ;
для
доли
;
для
доли
 .
При вероятности 0,683 коэффициент t
= 1;
при вероятности 0,954 коэффициент t
= 2;
при вероятности 0,997 коэффициент t
= 3.
Предельная ошибка выборки позволяет
определить предельные
значения характеристик генеральной
совокупности и их доверительные
интервалы:
для средней
.
При вероятности 0,683 коэффициент t
= 1;
при вероятности 0,954 коэффициент t
= 2;
при вероятности 0,997 коэффициент t
= 3.
Предельная ошибка выборки позволяет
определить предельные
значения характеристик генеральной
совокупности и их доверительные
интервалы:
для средней
 ;
;
 ;
для
доли
;
для
доли
 ;
;
 .
Наряду с абсолютным значением предельной
ошибки выборки рассчитывается также
и предельная
относительная ошибка выборки (процентное
отношение предельной ошибки выборки
к соответствующей характеристике
выборочной совокупности: для
средней), %:
.
Наряду с абсолютным значением предельной
ошибки выборки рассчитывается также
и предельная
относительная ошибка выборки (процентное
отношение предельной ошибки выборки
к соответствующей характеристике
выборочной совокупности: для
средней), %:
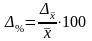 ;
для доли, %:
;
для доли, %: