13. Понятие доверительного интервала для среднего и доли генеральной совокупности и его определение по показателям выборки.

Выборочное наблюдение - это такой вид статистического наблюдения, при котором обследованию подвергается не вся изучаемая совокуп­ности, а лишь часть её единиц, отобранных в определённом порядке.

Вся исследуемая совокупность называется генеральной, а единицы, подлежащие наблюдению, составляют выборочную совокупность или выборку.

Цель выборочного наблюдения - определение параметров генераль­ной совокупности (генеральной средней и генеральной доли p) на осно­ве параметров выборочной совокупности (выборочной средней и выбо­рочной доли ω).

Разница между генеральными и выборочными параметрами называ­ется ошибкой выборки.

Различают два типа отбора: повторный и бесповторный. При по­вторном отборе после регистрации значений признаков единица возвра­щается в генеральную совокупность, а при бесповторном не возвращает­ся. В социально-экономической статистике, как правило, не применяется повторный отбор.

К наиболее распространённым на практике видам выборочного на­блюдения относятся:

• собственно случайная выборка;

• механическая выборка;

• типическая выборка;

• серийная выборка.

1. Собственно случайная выборка

Её суть заключается в том, что отбор единиц из генеральной сово­купности осуществляется наудачу, без каких-либо элементов системности. Все без исключения единицы генеральной совокупность имеют абсолютно равные шансы попасть в выборку.

Средняя ошибка собственно случайной выборки в случае повтор­ного отбора определяется по формуле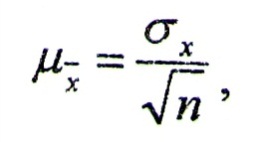

а для бесповторного отбора:

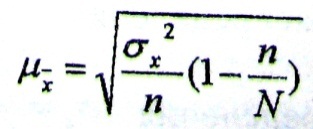
2. Механическая выборка

Данная выборка применяется в тех случаях, когда генеральная совокупность каким-либо образом упорядочена (табельные номера работни­ков, номера телефонов и т.п.). Устанавливается пропорция отбора, которая определяется соотношением объёмов выборочной и генеральной совокуп­ностей (например, отбирается каждая 50-я единица при соотношении 1:50). при решении задач на определение средней ошибки механической выборки, а также необходимой её численности, следует использовать при­ведённые выше формулы, применяемые при собственно случайном беспо­вторном отборе.

3. Типическая выборка

Эта выборка используется тогда, когда единицы генеральной сово­купности объединены в несколько крупных типических групп (например, при обследовании населения это районы, возрастные или социальные группы, отрасли промышленности и т.п.). Отбор единиц в выборку внутри этих групп производится пропорционально их объёму на основе исполь­зования собственно случайной или механической выборки.

Средняя ошибка типической выборки определяется по следующим формулам:

-для повторного отбора

-для бесповторного отбора , где 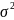- средняя из внутригрупповых дисперсий.

4) Серийная выборка

Эта выборка используется в тех случаях, когда единицы изучаемой совокупности объединены в небольшие равновеликие группы или серии. В выборочную совокупность отбираются серии с использованием собст­венно случайной или механической выборки. Внутри серий производится сплошное обследование единиц.

Средняя ошибка выборки определяется по следующим формулам: