36.Статистика трудовых ресурсов.

Трудовыми ресурсами считается та часть населения, которая фактически занята в экономике или не занята, но способна к труду по возрасту и состоянию здоровья.

В составе трудовых ресурсов выделяют следующие категории:

1) трудоспособное население в трудоспособном возрасте;

2) фактически работающих подростков моложе 16 лет;

3) фактически работающих лиц старше трудоспособного возраста.

Общую численность трудовых ресурсов можно рассчитать двумя методами.

В соответствии с первым методом в состав трудовых ресурсов включают население трудоспособного возраста за исключением инвалидов 1 и 2 групп и пенсионеров трудоспособного возраста, получающих пенсии по возрасту на льготных условиях, и прибавляют численность фактически работающих подростков и лиц пенсионного возраста.

В соответствии со вторым методом при определении численности трудовых ресурсов в рамках отдельных регионов учитывается также сальдо маятниковой миграции.

Сальдо маятниковой миграции рассчитывается как разность числа ежедневно приезжающих на работу в данный регион и возвращающихся к месту своего жительства в другие регионы и числа ежедневно уезжающих из данного региона к месту работы и возвращающихся обратно к месту своего жительства в данный регион.

Изменение численности трудовых ресурсов, не связанное с миграцией населения, называется естественным движением трудовых ресурсов. Естественное движение трудовых ресурсов характеризуется следующими показателями:

1) естественное пополнение трудовых ресурсов ПТРест происходит за счет вступления в трудоспособный возраст подростков, а также за счет привлечения к общественному труду пенсионеров и лиц в возрасте до 16 лет;

2) естественное выбытие трудовых ресурсов ВТРест происходит за счет смертности, перехода на пенсию или инвалидность, прекращения работы лицами нетрудоспособного возраста;

3) естественный прирост трудовых ресурсов ЕПТР рассчитывается как разность между естественным пополнением и естественным выбытием трудовых ресурсов:

ЕПТР= ПТРест — ВТРест.

Изменение численности трудовых ресурсов только за счет миграционных процессов называется механическим движением трудовых ресурсов.

Интенсивность изменения численности трудовых ресурсов характеризуют следующие показатели:

1) коэффициент естественного пополнения трудовых ресурсов:

где TP – среднегодовая численность трудовых ресурсов:

ТРi (i=1, n) – численность трудовых ресурсов на i-ую дату;

2) коэффициент естественного выбытия трудовых ресурсов:

3) коэффициент естественного прироста трудовых ресурсов:

Кест.пр. = Кест.поп. – Кест.выб.;

4) коэффициент миграционного прироста трудовых ресурсов:

где МП – миграционный прирост, определяемый на основе статистической отчетности.

26. Определение параметров уравнения тренда. Прогнозирование на основе тренда. Доверительный интервал прогноза.

Покажем пример подробного расчета параметров уравнения тренда на основе следующих данных (см. таблицу) с использованием калькулятора.

Линейное уравнение тренда имеет вид y = at + b. 1. Находим параметры уравнения методом наименьших квадратов. Система уравнений МНК: a₀n + a₁∑t = ∑y a₀∑t + a₁∑t² = ∑y•t

Прогнозирование на основе тренда

Прогнозирование возможных в будущем значений признаков изучаемого объекта - одна и основных задач науки. В ее решении роль статистических методов очень значительна. Одним из статистических методов прогнозирования является расчет прогнозов на основе тренда и колеблемости динамического ряда до настоящего времени. Методика статистического прогноза по тренду и колеблемости основана на их экстраполяции, т.е. на предположении, что параметры тренда и колебаний сохраняются до прогнозируемого периода. Такая экстраполяция справедлива, если система развивается эволюционно в достаточно стабильных условиях. Чем крупнее система, тем более вероятно сохранение параметров ее изменения, конечно, на срок не слишком большой! Обычно рекомендуют, чтобы срок прогноза не превышал одной трети длительности базы расчета тренда.

В отличие от прогноза на основе регрессионного уравнения прогноз по тренду учитывает факторы развития только в неявном виде, и это не позволяет «проигрывать» разные варианты прогнозов при разных возможных значениях факторов, влияющих на изучаемый признак. Зато прогноз по тренду охватывает все факторы, в то время как в регрессионную модель невозможно включить в явном виде более 10-20 факторов в самом лучшем случае.

Средняя ошибка прогноза положения линейного треида на год (момент) с номером tk вычисляется по формулам:

А) • Для однократного выравнивания:

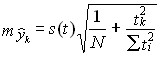                                                             (9.48)

где    tk - номер года прогноза,

          Σti2 - по всей длине ряда N, т. е. .

Б) • Для многократного скользящего выравнивания При/сдвигах базы и длине ее n:

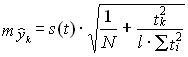                                       (9.49)

где    .

Однако, фактические уровни ряда отклоняются от тренда. Ошибка прогноза конкретного уровня включает две неопределенности: во-первых, мы не знаем точно, где окажется тренд ., а во-вторых - в какую сторону и на сколько уровень ряда отклонится от положения тренда. Считая, как уже было сказано, колебания случайно (в основном, случайно) распределенными во времени, т. е. независимыми от тренда, определим ошибку прогноза уровня конкретного года по правилу сложения независимых дисперсий.

                                                                 (9.50)

Методика анализа и прогнозирования тоже имеет значение. Она определяет степень полноты извлечения информации, содержащейся в исходном ряду динамики. С помощью методики многократного выравнивания удается более полно извлечь информацию о тренде и уменьшить среднюю ошибку прогноза его положения в прогнозируемом периоде. Однако, как видно из (9.50), главной составляющей ошибки прогноза конкретного уровня в нашем расчете является не ошибка прогноза положения тренда, а колеблемость уровней около тренда. Поэтому ошибка прогноза конкретного уровня незначительно сократилась за счет многократного выравнивания. При слабой колеблемости уровней и прогнозировании на значительное удаление от базы, главную роль станет играть ошибка положения тренда. Тогда многократное выравнивание даст значительное сокращение средней ошибки прогноза конкретных уровней. Но в любом случае эта ошибка всегда больше показателя колеблемости уровней - среднего квадратического отклонения Sy(t)1

. В частности, в указанной литературе содержатся формулы для вычисления средней ошибки прогноза положения линии тренда при параболической и экспоненциальной его формах2

. Если средняя ошибка положения тренда вычислена, ошибку конкретного уровня при любой форме тренда вычисляют по формуле (9.50).

Доверительный интервал прогноза

Одна из основных задач, возникающих при прогнозировании, заключается в определении доверительных интервалов прогноза. Интуитивно понятно, что в основе расчета доверительности интервала прогноза должен быть положен измеритель колеблемости ряда. Чем выше эта колеблемость, тем шире интервал для прогноза. Следовательно, вопрос о доверительном интервале прогноза следует начать с рассмотрения измерителя колеблемости. Обычно таким измерителем является среднее квадратическое отклонение:

,

где - соответственно фактическое и расчетное значения ряда;

f – число степеней свободы, определяемое в зависимости от числа наблюдений (n) и числа оцениваемых параметров.

f = n – z,

где z – число оцениваемых параметров.

Например, для параболы второй степени f = n – 3, третьей степени f = n – 4 и т.д.

Сумму квадратов отклонений от тренда можно разложить следующим образом:

Последнее выражение можно упростить. Допустим, что начало отсчета находится в середине ряда, тогда , а параметры а и b будут равны:

; .

После преобразований получим:

Разность первых двух членов правой стороны равна сумме квадратов отклонений от средней арифметической, т.е. .

Таким образом,

Последнее выражение показывает, что сумма квадратов отклонений от линий тренда меньше, чем от средней арифметической.

Сумма квадратов отклонений от линий тренда, т.е. и среднее квадратическое отклонение от тренда Sy является основой при определении средней квадратической ошибки параметров.

Прежде чем приступить к определению доверительного интервала прогноза, следовало бы сделать оговорку. Дело в том, что предположение о нормальности распределения отклонений вокруг линии регрессии не может ни утверждаться и не быть проверено при анализе рядов. Дискуссии еще в 30-40-х годах пролили свет на трудности, связанные с этой проблемой. В итоге, принципиальный новый подход так и не был найден. Все предложения так или иначе связаны с определением доверительного интервала на основе оценки среднего квадратического отклонения членов ряда.

Полученные в ходе оценивания параметры не свободны от погрешности. Расчетные значения несут на себе груз неопределенности, связанной с ошибками в значении параметров.

В общем виде доверительный интервал прогноза определяется как

,

где - средняя квадратическая ошибка;

- расчетное значение у_t;

- значение t-критерия Стьюдента.

Если t = I + L, то последнее определит значение доверительного интервала на L единиц времени.

Доверительный интервал прогноза должен учитывать не только неопределенность, но возможность отклонения, т.е. диапазон варьирования. Если обозначим среднюю квадратическую ошибку как S_p, тогда доверительный интервал прогноза составит:

28. Понятие индексов. Индивидуальные индексы. Агрегатные индексы и средние из индивидуальных.

Индекс (Index) означает указатель, показатель.

В статистике индекс – это относительная величина, характеризующая изменения во времени и в пространстве уровня изучаемого общественного явления (процесса), или степень выполнения плана.

Индивидуальные индексы характеризуют соотношение отдельных элементов совокупности.

Индивидуальный индекс обозначается буквой Он определяется методом сопоставления двух величин, характеризующих уровень исследуемого статистического процесса или явления во времени или в пространстве, т. е. за два сравниваемых периода. Период (уровень которого сравнивается) называется отчетным, или текущим, периодом и обозначается подстрочным знаком «I», а период, с уровнем которого проводится сравнение, называется базисным и обозначается подстрочным знаком «О» или «ря», если при внутрифирменном планировании сравнение проводится с планом. Если изменение явлений изучается за ряд периодов, то каждый период обозначается соответственно подстрочным знаком «О», «1», «2», «3» и т. д.

В статистике количество обозначают буквой «q», цену – «р», себестоимость – «z», затраты времени на производство единицы продукции – «t».