Виды дисперсий и правило их сложения. Свойства дисперсии.
Свойство 1. Дисперсия постоянной величины равна нулю.
Свойство 2. Уменьшение (увеличение) всех значений признака на одну и ту же величину А не меняет величины дисперсии.
Свойство 3. Уменьшение (увеличение) всех значений признака в k раз уменьшает (увеличивает) дисперсию в k² раз, а среднее квадратическое отклонение - в k раз.
Для целей сравнения колеблемости различных признаков в одной и той же совокупности или же при сравнении колеблемости одного и того же признака в нескольких совокупностях представляют интерес показатели вариации, приведенные в относительных величинах. Базой для сравнения должна служить средняя арифметическая. Эти показатели вычисляются как отношение размаха вариации, среднего линейного отклонения или среднего квадратического отклонения к средней арифметической или медиане. Чаще всего они выражаются в % и определяют не только сравнительную оценку вариации, но и дают характеристику однородности совокупности. Совокупность считается однородной, если коэффициент вариации не превышает 33% (для распределений, близких к нормальному).
Различают следующие относительные показатели вариации (V):
Коэффициент
осцилляции (
):
отражает относительную колеблемость
крайних значений признака вокруг средней
Линейный
коэффициент вариации ( ):
характеризует долю усреднённого значения
абсолютных отклонений признака от средней величины
Коэффициент
вариации ( ):
используется для оценки типичности
средних величин
Наряду с изучением вариации признака по всей совокупности в целом часто бывает необходимо проследить количественные изменения признака по группам, на которые разделяется совокупность, а также и между группами. Такое изучение вариации достигается посредством вычисления и анализа различных видов дисперсии. Выделяют:
дисперсию общую
межгрупповую
внутригрупповую.
Общая дисперсия измеряет вариацию признака во всей совокупности под влиянием всех факторов, обусловивших эту вариацию:
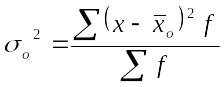
где хо – общая средняя арифметическая для всей изучаемой совокупности.
Межгрупповая дисперсия ( ) характеризует систематическую вариацию, т. е. различия в величине изучаемого признака возникающие под влиянием признака-фактора, положенного в основание группировки.
Рассчитывается по формуле:
где
-
средняя по отдельной группе;
ni – число единиц в определенной группе.
Внутригрупповая дисперсия ( ) отражает случайную вариацию, т. е. часть вариации, происходящую под влиянием неучтенных факторов и не зависящую от признака-фактора, положенного в основание группировки.
Рассчитывается
по формуле:
На
основании внутригрупповой дисперсии
по каждой группе можно определить общую
среднюю из внутригрупповых дисперсий
( ):
Указанные
дисперсии взаимосвязаны между собой
следующим равенством: величина общей
дисперсии равна сумме средней из
внутригрупповых и межгрупповой дисперсий:
соотношение
называют правилом сложения дисперсии.
Согласно этому правилу, общая дисперсия,
возникающая под действием всех факторов,
равна сумме дисперсии, появляющейся
под влиянием всех прочих факторов, и
дисперсии, возникающей за счет
группировочного признака.
В
статистическом анализе широко используется
показатель, представляющий собой долю
межгрупповой дисперсии в общей дисперсии
- эмпирический коэффициент детерминации
( ):
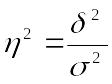показывает
долю (удельный вес) общей вариации
изучаемого признака, обусловленную
вариацией группировочного признака.
Корень квадратный из эмпирического коэффициента детерминации – это эмпирическое корреляционное отношение ( ):
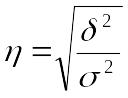
характеризует
влияние признака, положенного в основание
группировки (группировочного), на
вариацию результативного признака.
Эмпирическое корреляционное отношение
изменяется в пределах от 0 до 1.
Если
= 0, то группировочный признак не
оказывает влияния на результативный.
Если
= 1, то результативный признак изменяется
только в зависимости от признака,
положенного в основание группировки,
а влияние прочих факторных признаков
равно нулю.
Промежуточные значения
оцениваются в зависимости от их близости
к предельным значениям.
Кривые распределения. Показатели формы распределения.
Ряды динамики: понятие, виды, составные элементы.
Показатели анализа рядов динамики.
Структура ряда динамики. Сглаживание рядов динамики с помощью скользящей средней.
Аналитическое выравнивание ряда динамики. Интерполяция и экстраполяция.
Понятие и значение экономических индексов, их виды. Правило построения агрегатных индексов количественных и качественных показателей.
Индексы физического объема, цен, стоимости продукции, их взаимосвязь.
Индексы производительности труда, затрат времени на производство продукции.
Индексы себестоимости продукции и издержек производства. Их взаимосвязь.
Изучение динамики качественных показателей по нескольким единицам (индексы переменного состава, постоянного состава, структурных сдвигов).
Использование индексного метода в изучении взаимосвязи экономических явлений.
Виды связей между социально-экономическими явлениями. Задачи корреляционного и регрессионного анализа.
Показатели тесноты связи в парной корреляции между количественными признаками.
Показатели тесноты связи в парной корреляции между качественными признаками.
Множественная корреляционная зависимость. Определение тесноты связи между признаками. Коэффициенты эластичности.
Понятие выборочного наблюдения и его виды. Значение выборочного метода в статистике.
Генеральная и выборочная совокупности, их характеристики.
Формы организации выборочного наблюдения.
Ошибки наблюдения.
Система национальных счетов и баланс народного хозяйства.
Основные счета внутренней экономики и их взаимосвязь в СНС.
Основные макроэкономические показатели Системы национальных счетов.
Классификация секторов внутренней экономики.
Методы определения валового внутреннего продукта.
Понятие национального богатства. Классификация активов национального богатства.
Понятие и классификация основных фондов.
Виды оценки основных фондов.
Показатели движения, состояния и использования основных фондов.
Показатели объема, структуры и использования оборотных фондов.
Определение потребности в основных оборотных фондах.