11. Структурные средние. Их расчет в дискретном и интервальном рядах распределения.

Структурные средние - мода и медиана - в отличие от степенных средних, которые в значительной степени являются абстрактной характеристикой совокупности, выступают как конкретные величины, совпадающие с вполне определенными вари­антами совокупности.

Модой называется значение признака, которое наиболее часто встречается в совокупности (в статистическом ряду).

Для совокупности 3;4;2;4;3;3 мода равна 3

Медианой называется значение признака, которое лежит в середине ранжированного ряда и делит этот ряд на две равные по численности части. Если число n вариант нечётно, то медиана равна варианте под номером (n + 1)/2

12. Математические свойства средней величины. Расчет средней арифметической по способу моментов.

Средняя арифметическая обладает некоторыми математическими свойствами, более полно раскрывающими ее сущность и в ряде случаев используемыми при ее расчетах.

Произведение средней на сумму частот равно сумме произведений отдельных вариантов на соответствующие им частоты:

Сумма отклонений индивидуальных значений признака от средней арифметической равна нулю:

3. Если все осредняемые варианты уменьшить или увеличить на постоянное число А, то средняя арифметическая соответственно уменьшится или увеличится на ту же величину:

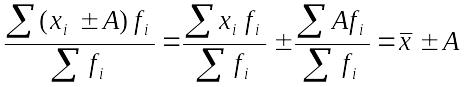
4. Если все варианты значений признака уменьшить или увеличить в А раз, то средняя также соответственно увеличится или уменьшится в А раз:

5. Если все веса уменьшить или увеличить в А раз, то средняя арифметическая от этого не изменяется:

13. Вариация признака в совокупности, ее значение и изучение. Абсолютные и относительные показатели вариации.

Конкретные условия в которых находится каждый из изучаемых объектов, а также особенности их собственного развития (социальные, экономические и пр.) выражаются соответствующими числовыми уровнями стат. показателей.

Т. О., вариация, т.е. несовпадение уровней одного и того же показателя у разных объектов имеет объективный характер и помогает познать сущность изучаемого явления. Для измерения вариации в статистике применяют несколько способов.

Размах вариации (R) – это разность между наибольшим и наименьшим наблюдаемыми значениями.

R = Xmax – Xmin

Более строгими характеристиками являются показатели колеблемости относительно среднего уровня признака.

2. Простейший показатель такого типа – среднее линейное отклонение. Оно вычисляется как средняя арифметическая из абсолютных значений отклонений вариант хi, и (взвешенная или простая в зависимости от исходных условий) по следующим формулам:

для несгруппированных данных:

где n – число членов ряда;

для несгруппированных данных:

где - сумма частот вариационного ряда.

Поскольку сумма отклонений значений признака от средней величины равна нулю, приходится все отклонения брать по модулю, на что указывают прямые скобки в числителе формул

3.Дисперсия представляет собой средний квадрат отклонений индивидуальных значений признака от их средней величины и вычисляется по формулам простой и взвешенной дисперсий (в зависимости от исходных данных):

простая дисперсия для несгруппированных данных:

взвешенная дисперсия для сгруппированных данных:

Формула для расчета дисперсии может быть преобразована в т.е. дисперсия равна средней из квадратов индивидуальных значений признака минус квадрат средней величины.

Дисперсия есть средняя величина квадратов отклонений.

4. Если извлечь корень из дисперсии получим среднее квадратическое отклонение:

для несгруппированных данных

для сгруппированных данных

Среднее квадратическое отклонение - это обобщающая характеристика размеров вариации признака в совокупности. Оно выражается в тех же единицах измерения, что и признак (в метрах, тоннах, рублях, процентах и т. д.).