Понятие о средних величинах, их значение. Виды средних величин и их расчет.
Средняя величина — это обобщающий показатель, характеризующий типичный уровень варьирующего количественного признака на единицу совокупности в определенных условиях места и времени.
Объективность и типичность статистической средней обеспечивается лишь при определенных условиях.
Первое условие - средняя должна вычисляться для качественно однородной совокупности. Для получения однородной совокупности необходима группировка данных, поэтому расчет средней должен сочетаться с методом группировок.
Второе условие - для исчисления средних должны быть использованы массовые данные. В средней величине, исчисленной на основе данных о большом числе единиц (массовых данных), колебания в величине признака, вызванные случайными причинами, погашаются и проявляется общее свойство (типичный размер признака) для всей совокупности.
Средняя величина всегда именованная, она имеет ту же размерность, что и признак у отдельных единиц совокупности.
При использовании средних в практической работе и научных исследованиях необходимо иметь в виду, что за средним показателем скрываются особенности различных частей изучаемой совокупности, поэтому общие средние для однородной совокупности должны дополняться групповыми средними, характеризующими части совокупности.
Средние величины делятся на два больших класса:
степенные средние, относятся такие наиболее известные и часто применяемые виды, как средняя геометрическая, средняя арифметическая и средняя квадратическая.
структурные средние. рассматриваются мода и медиана.
Степенные средние в зависимости от представления исходных данных могут быть:
простыми
взвешенными
Простая средняя считается по несгруппированным данным и имеет следующий общий вид:
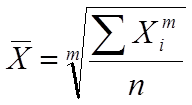
где
хi - варианта (значение) определенного признака,
m – показатель степени средней.
n – число вариант (значений).
Взвешенная средняя считается по сгруппированным данным и имеет вид:
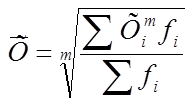
где
хi - варианта (значение) определенного признака или серединные значения интервала, в котором измеряется варианта,
m – показатель степени средней.
fi – частота, показывающая сколько раз встречается i-е значение осредняемого признака.
Общие формулы расчета степенных средних имеют показатель степени m.
В зависимости от того, какое значение он принимает, различают следующие виды степенных средних:
средняя гармоническая, если m = -1
средняя геометрическая, если m > 0
средняя арифметическая, если m = 1
средняя квадратическая, если m = 2
средняя кубическая, если m = 3
Средняя арифметическая и средняя гармоническая наиболее распространенные виды средней, получившие широкое применение в плановых расчетах, при расчете общей средней из средних групповых, а также при выявлении взаимосвязи между признаками с помощью группировок. Выбор средней арифметической и средней гармонической определяется характером имеющейся в распоряжении исследователя информации.
Средняя квадратическая применяется для расчета среднего квадратического отклонения ( σ ), являющегося показателем вариации признаков, а также в технике (например, при сооружении трубопроводов).
Средняя геометрическая (простая) используется при вычислении среднего коэффициента роста (темпа) в рядах динамики.