Точечные и интервальные оценки законов распределения результатов наблюдений

При анализе же дискретных случайных величин возникает задача нахождения точечных оценок параметров их функции распределения на основании выборок — ряда значений хi, принимаемых случайной величиной х в п независимых опытах.  Оценку параметра называют точечной, если она выражается одним числом. К точечным характеристикам погрешности относятся СКО случайной погрешности и среднее арифметическое значение измеряемой величины.  Задача нахождения точечных оценок — частный случай статистической задачи определения оценок параметров функции распределения случайной величины на основании выборки. В отличие от самих параметров их точечные оценки являются случайными величинами, значения которых зависят от объема экспериментальных данных, а закон распределения — от законов распределения самих случайных величин.  К точечным оценкам предъявляются требования состоятельности, несмещенности и эффективности.  Состоятельной называется оценка, которая при увеличении объема выборки стремится по вероятности к истинному значению числовой характеристики.  Несмещенной называется оценка, математическое ожидание которой равно оцениваемой числовой характеристике. Эффективной считают ту из нескольких возможных несмещенных оценок, которая имеет наименьшую дисперсию.  Оценим математическое ожидание m и СКО σ для ограниченной группы (выборки) наблюдений, обозначив их через  хi Результат измерений при распределении наблюдений по нормальному закону определяют, учитывая известную в теории вероятностей закономерность (закон больших чисел): при достаточно большом числе n независимых наблюдений хiсреднее арифметическое значений случайной величины приближается к ее математическому ожиданию топределяемому подобно оценке по формуле

                                   (4.26)

Соответственно, при оценке СКО σ используют выражение для СКО σ, справедливое для достаточно больших п:

                                  (4.27)

Для оценки рассеяния отдельных результатов измерения (хi) относительно среднего арифметического значения   определяют оценку СКО этого среднего арифметического

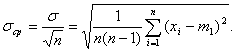                             (4.28)

Применение формулы (4.28) правомерно при условии постоянства измеряемой величины х в процессе измерения. Если при измерении величина х изменяется, как, например, при измерении потенциала проводника через равные отрезки длины, то в формуле (4.28) в качестве т следует брать какую-то постоянную величину, например, начало отсчета.  Формулы (4.27) и (4.28) связаны соотношением

                                                (4.29)

Среднее арифметическое значение из ряда измерений всегда имеет меньшую погрешность, чем погрешность каждого отдельного измерения. Это и отражает формула (4.29), определяющая фундаментальный закон теории погрешностей, из которого следует, что если требуется повысить точность результата (при исключенной систематической погрешности) в 2 раза, то число измерений нужно увеличить в 4 раза; если необходимо повысить точность в 3 раза, то число измерений увеличивается в 9 раз и т. д. При этом необходимо четко разграничивать применение средних квадратических отклонений σ ср и σ: величину σ ср применяют при оценке погрешностей окончательного результата, σ — при оценке погрешности метода измерения.