
- •Классификация погрешностей
- •По характеру проявления
- •Погрешность прямых измерений - вычисляется по формуле
- •Погрешность измерения и принцип неопределенности Гейзенберга.
- •Классификация и основные характеристики измерений
- •Основные характеристики, виды, методы и методики измерений
- •Качество, точность и погрешности измерений
- •Систематические погрешности
- •Методы исключения систематических погрешностей
- •Случайные погрешности
- •Точечные и интервальные оценки законов распределения результатов наблюдений
- •4.7 Прямые многократные измерения
- •4.8. Прямые однократные измерения
- •4.9. Косвенные измерения
- •Анализ формулы (4.56) позволяет получить простые правила оценивания погрешности результата косвенного измерения.
- •4.10. Совместные измерения
Анализ формулы (4.56) позволяет получить простые правила оценивания погрешности результата косвенного измерения.
Правило 1. Погрешности в суммах и разностях. Если аргументы (для упрощения возьмем два) x1 и х2 измерены с погрешностями Δх1 и Δх2 и измеренные значения используются для вычисления суммы или разности А=х1 ± х2, то суммируют абсолютные погрешности без учета знака: ΔA= Δх1 + Δх2.
Правило 2. Погрешности в произведениях и частных. Если измеренные значения х1 и х2 используют для вычисления А = x1 • x2, или А=x1/х2, то суммируют относительные погрешности δА=δх1 + δx2, где δx = Δх/х.
Правило 3. Измеренная величина умножается на константу. Если* используют для вычисления произведения A = В•x, в котором В не имеет погрешности, то δА = δх.
Правило 4. Возведение в степень. Если аргумент х используют для вычисления степени А = х^n, то δA = nδх.
Правило 5. Погрешность в произвольной функции одной переменной. Если величину х используют для вычисления функции А(х), то относительная погрешность
![]() (4.57)
(4.57)
4.10. Совместные измерения
Совместными называют выполняемые одновременно измерения двух или нескольких неодноименных физических величин с целью установления зависимости между ними. Пусть требуется определить зависимость у =f(x) между параметрами х и у. Для этого необходимо изменять величину х и при каждом ее установленном значении выполнять одновременное измерение величин х и у. В результате подобных измерений находят координаты (xi, уi) искомой зависимости y=f(x). Экспериментальные координаты хi, уi(где i = 1,2, ... , n — число совместных измерений) отличаются от истинных координат (х, у) из-за систематических и случайных погрешностей. Поэтому возникает задача наилучшей аппроксимации экспериментальной зависимости у =f(x) по координатам хi,уi. Оптимальный подход к решению подобных задач возможен на основе применения метода наименьших квадратов. Метод наименьших квадратов. В математике это один из методов теории ошибок для оценки неизвестных величин по результатам измерений, содержащим случайные погрешности. Данный метод применяют и для приближенного представления заданной Функции более простыми функциями. Суть метода наименьших квадратов состоит в том, что наивероятнейшими значениями аргументов искомой аналитической зависимости будут те, при которых сумма квадратов отклонений экспериментальных значений функции уi от значений самой функции у будет наименьшей
![]() (4.59)
(4.59)
Пусть у является функцией нескольких аргументов:
y=f(xi,a,b,c,...,s),
где а, b, с, ... , s— неизвестные коэффициенты. Тогда на основании n экспериментальных пар yi и хi следует определить т+1 искомых аргументов аналитической зависимости, которая наилучшим образом описывает массив уiи хi, т. е. метод наименьших квадратов требует выполнения условия
![]() (4.60)
(4.60)
На основе метода наименьших квадратов можно проводить аппроксимацию различных аналитических зависимостей, например, выражаемых полиномами вида: у - а + bх + сх2 +...+ sxn, где коэффициенты а, b, с, ... , s— константы. Рассмотрим важный для практики случай, когда искомая зависимость имеет линейный характер вида
у = а + bх.(4.61)
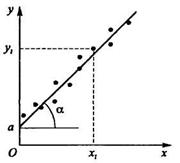
Рис. 4.8. Аппроксимация исследуемой зависимости
При использовании метода наименьших квадратов необходимо по набору из п экспериментальных координат (хi, уi) найти такие оценки неизвестных постоянных а и b, при которых получают прямую, наилучшим образом отражающую истинную анализируемую линию. График функции (4.61) представляет собой прямую линию с коэффициентом b = tgα, пересекающую ось ординат в точке у = а (рис. 4.8). В соответствии с методом наименьших квадратов наилучшим оценкам искомым постоянным а и Ь соответствует минимальное значение следующего выражения:
![]() (4.62)
(4.62)
где [уi- (а + bхi)] — отклонение измеренных значений у, от вычисленных по формуле (4.61) при х = хi. Из курса математики известно, что
![]() (4.63)
(4.63)
Здесь коэффициенты
![]()
![]()
![]()
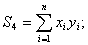
![]() (4.64)
(4.64)
Степень приближения найденных значений постоянных а и bк истинным значениям этих коэффициентов оценивают с помощью их СКО σ а и σ ь;
![]()
![]() (4.65)
(4.65)
где σ у — СКО погрешности измерения величины у, значение которой можно получить из паспортных данных на средство измерения или вычислить по формуле:
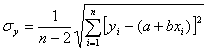 (4.66)
(4.66)
