4.9. Косвенные измерения
Напомним, что при косвенных измерениях измеряемая физическая величина A является известной функцией ряда других измеряемых величин — аргументов x1, х2, ..., хi, ... , хm. Аргументы, т. е. перечисленные измеряемые величины, подвергаются прямым измерениям, а величину А вычисляют по формуле
(4.50)
Каждый из аргументов измеряется с некоторой погрешностью, вносящей определенный вклад в результат косвенного измерения. Для оценки этих погрешностей важно разделение косвенных измерений на линейные и нелинейные косвенные измерения. При линейных косвенных измерениях формула (4.50) запишется в следующем виде:
(4.51)
где bi— постоянные коэффициенты при искомых аргументах хi,
В случае нелинейных косвенных измерений соотношение (4.50) будет представлять собой уже другие, отличные от (4.51), функциональные зависимости. Погрешности измерения аргументов могут быть заданы либо своими границами Δх i либо доверительными границами Δx(Рд)i с доверительными вероятностями РДi. Если число аргументов невелико (меньше пяти), то простая оценка погрешности результата ΔA получается суммированием предельных погрешностей (без учета знака), т.е. подстановкой границ Δх1, Δx2,... , Δхm в формулу
(4.52)
На
практике эта оценка завышена, поскольку
подобное суммирование сводится к
тому, что погрешности измерения всех
аргументов одновременно совпадают по
знаку и имеют максимальное значение.
Обычно вероятность такого совпадения
близка к нулю. Чтобы найти более
реалистичную оценку, проводят
статистическое суммирование погрешностей
аргументов. Полагая, что в заданных
границах погрешности аргументов
распределены равномерно, доверительные
границы ΔA(РД) погрешности результата
косвенного измерения рассчитывают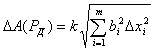 к
ак
(4.53)
Здесь коэффициент к определяют так же, как и аналогичные коэффициенты для формулы (4.42). Если погрешности измерения аргументов заданы доверительными границами с одинаковыми доверительными вероятностями, то, считая распределение этих погрешностей нормальным, доверительные границы находят по формуле
(4.54)
При нелинейных косвенных измерениях возникают существенные сложности статистической обработки результатов и Погрешностей, связанные с изменением законов распределения аргументов хi при их функциональных преобразованиях. Поэтому проводят приближенную оценку погрешности результата косвенного измерения на основе линеаризации функции (4.50).
Запишем выражение для полного дифференциала функции А через частные производные по аргументам хi:
(4.55)
Согласно известному в математике определению, полный дифференциал функции является приращением этой функции, вызванным малыми приращениями ее аргументов. Поскольку погрешности измерения аргументов всегда величины малые по сравнению с номинальными значениями аргументов, то справедлива замена в (4.55) дифференциалов аргументов dx, на погрешности измерений Ахi, а дифференциала функции dA на погрешность результата измерения ДЛ:
(4.56)