Зміст
1. Вступ 2
4
1.1. Способи представлення графів в пам'яті ЕОМ 4
2. Постановка задачі 5
3. Вхідні данні 6
4. Вхідні форми 7
5. Вхідний формат текстового файла 8
6. Вихідні данні 9
7. Вихідні форми 9
8. Метод вирішення 10
9. Аномалії 11
10. Функціональні тести 12
11. Нисхідна проектування 14
Література 42
Вступ
При вирішенні багатьох завдань, що зустрічаються в комп'ютерних науках, математиці, техниче ¬ ських дисциплінах, часто виникає необхідність наочного подання відно ¬ шений між якими об'єктами. Гра ¬ фи - природна модель для таких відносин. Вони широко застосовуються для алгоритмічного дослідження структур дискретних систем.
Граф - сукупність безлічі V вершин і безлічі Е зв'язків між ними, яка позначається G = (V, Е). Зв'язок, що має напрям, називається дугою, в іншому випадку - ребром.
Граф, у якого всі зв'язки - ребра, називається неорієнтованим (або неорграфом).
Діаметр графа - це максимальне з відстаней між парами його вершин. Відстань між вершинами визначається як найменше число ребер, які необхідно пройти, щоб дістатися з однієї вершини в іншу. Інакше кажучи, це відстань між двома вершинами графа, максимально віддаленими один від одного. Висячої (або листом) вершина називається, якщо вона є кінцем рівно одного ребра.
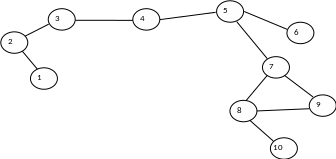
Малюнок 1.1 – Неорієнтований граф
Неорієнтованим графом називається зв'язаним, якщо для будь-якої пари вершин існує шлях з однієї в іншу. Для неорграфа відносин «бути досяжним з» є відношенням еквівалентності на множині вершин. Класи еквівалентності називаються пов'язаними компонентами графа. Неорієнтовані граф пов'язаний тоді і тільки тоді, коли він складається з єдиної пов'язаної компоненти. Незв'язаний граф складається принаймні з двох компонент пов'язаності.
1.1. Способи представлення графів в пам'яті еом
Для представлення графів можна використовувати різні структури даних. Вибір структури даних залежить від операторів, які будуть застосовуватися до вершин і ребрах (дугам) графа.
Матриця смежностей графа
Одним з найбільш загальних уявлень орграфа G = (V, Е) є матриця суміжності. Припустимо, що безліч вершин V = {1, 2, ..., n}. Матриця суміжності для орграфа G - це матриця розмі ¬ ра n х n із значеннями булевого типу, де A [i, j] = true тоді і тільки тоді, коли існує дуга з вершини i в вершину j. Часто в матрицях суміжності значення true замінюється на 1, а значення false - на 0. Час доступу до елементів матриці суміжності залежить від розмірів множини вершин і безлічі дуг.
Для неорграфа матриця симетрична щодо головної діагоналі і сума елементів матриці в кожному рядку і в кожному стовпці дорівнює ступенями відповідних вершин.
Масив FI формується так: спочатку записують номери вершин (в будь-якому порядку), з яких виходять дуги в першу вершину, потім ставлять роздільник 0, далі записують номери вершин, з яких виходять дуги в другу вершину, і ставлять роздільник 0 і т.д. Таким чином, для неорграфа і мультіграф будується масив FI довжиною 2xт + N, оскільки кожне ребро враховується двічі.
Приклад Fi представлення для графа на мал.1:
Таблица 1
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
1 |
|
1 |
|
|
|
|
|
|
|
|
2 |
1 |
|
1 |
|
|
|
|
|
|
|
3 |
|
1 |
|
1 |
|
|
|
|
|
|
4 |
|
|
1 |
|
1 |
|
|
|
|
|
5 |
|
|
|
1 |
|
1 |
1 |
|
|
|
6 |
|
|
|
|
1 |
|
1 |
|
|
|
7 |
|
|
|
|
1 |
1 |
|
1 |
1 |
|
8 |
|
|
|
|
|
|
1 |
|
1 |
1 |
9 |
|
|
|
|
|
|
1 |
1 |
|
|
10 |
|
|
|
|
|
|
|
1 |
|
|
Завдання графа масивом попередником вершин (Fi - подання).
FI-виставу для графа 1.2 буде виглядати так:
Fi = {2 0 1 3 4 6 0 2 4 0 2 3 5 9 0 4 0 2 7 8 0 6 0 6 9 0 4 8 10 0 9 0}