2. Расчет параметров линейной регрессии

Рассмотрим методику расчета параметров линейной регрессии на конкретном примере.

По группе предприятий, выпускающих один и тот же вид продукции, рассматривается функция издержек

Необходимая для расчета оценок параметров и информация представлена в расчетной таблице 1.

Таблица 1–Расчетная таблица

Номер предприятия	Выпуск продукции, тыс.ед.	Затраты на производство, млн. руб.
1	1	30	30	1	900	31,1
2	2	70	140	4	4900	67,9
3	4	150	600	16	22500	141,6
4	3	100	300	9	10000	104,7
5	5	170	850	25	28900	178,4
6	3	100	300	9	10000	104,7
7	4	150	600	16	22500	141,6
Итого

Система нормальных уравнений будет иметь вид:

Решив ее, получим:

Запишем уравнение регрессии:

Подставив в уравнение значения , найдем теоретические значения (последняя графа таблицы 1). В данном случае ве­личина параметра не имеет экономического смысла.

В рассматриваемом примере имеем:

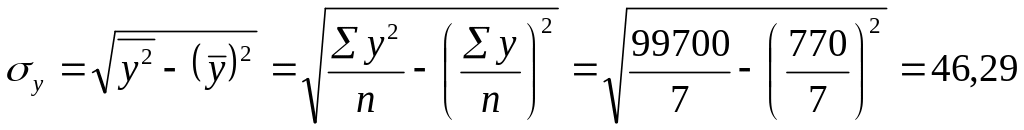
То, что < 0, соответствует опережению изменения результа­та над изменением фактора > .

3.Экономический смысл и содержание показателей тесноты связи в линейных моделях

Уравнение регрессии всегда дополняется показателем тесно­ты связи. При использовании линейной регрессии в качестве та­кого показателя выступает линейный коэффициент корреляции .

Имеются разные модификации формулы линейного коэффи­циента корреляции, например:

, (12)

Как известно, линейный коэффициент корреляции находит­ся в границах:

–1 ≤ ≤ 1

Если коэффициент регрессии > 0, то 0 ≤ ≤ 1

Если коэффициент регрессии < 0, то –1 ≤ ≤ 0

По данным таблицы 1 величина линейного коэффициента кор­реляции составила:

Это означает наличие очень тесной за­висимости затрат на производство от величины объема выпущен­ной продукции.

Следует иметь в виду, что величина линейного коэффициента корреляции оценивает тесноту связи рассматриваемых признаков в ее линейной форме. Поэтому близость абсолютной величины линейного коэффициента корреляции к нулю еще не означает от­сутствия связи между признаками.

При иной спецификации мо­дели связь между признаками может оказаться достаточно тесной.

Для оценки качества подбора линейной функции рассчиты­вается квадрат линейного коэффициента корреляции назы­ваемый коэффициентом детерминации.

Коэффициент детермина­ции характеризует долю дисперсии результативного признака у, объясняемую регрессией, в общей дисперсии результативного признака:

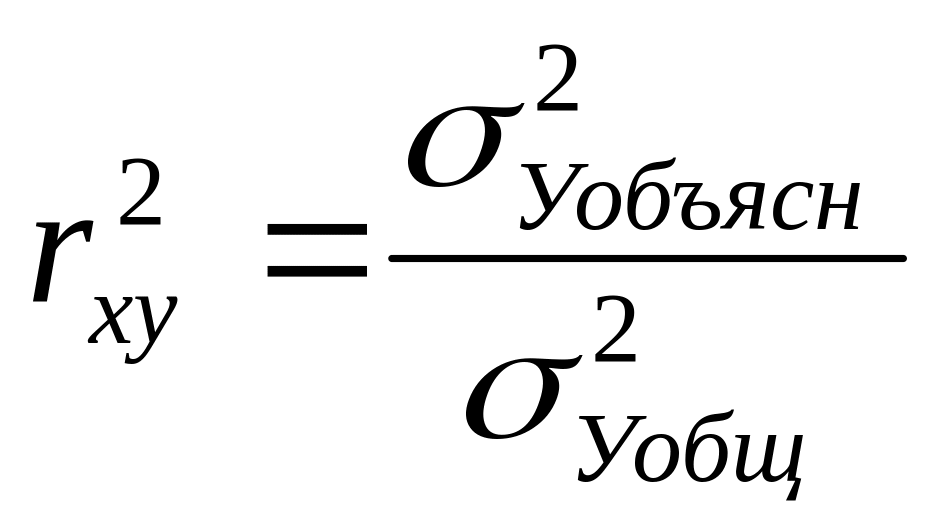, (13)

Соответственно величина характеризует долю диспер­сии , вызванную влиянием остальных, не учтенных в модели факторов.

В нашем примере . Таким образом, уравнением регрессии объясняется 98,2 % дисперсии результативного признака, а на долю прочих факторов приходится лишь 1,8 % ее дисперсии (то есть остаточная дисперсия).

Величина коэффициента детермина­ции является одним из критериев оценки качества линейной мо­дели. Чем больше доля объясненной вариации, тем соответствен­но меньше роль прочих факторов и, следовательно, линейная мо­дель хорошо аппроксимирует исходные данные, и ею можно воспользоваться для прогноза значений результативного признака.

Так, полагая, что объем продукции предприятия, составляет 5 тыс. ед., прогнозное значение для издержек производства составит 178,4 тыс. руб.

Линейный коэффициент корреляции по содержанию отлича­ется от коэффициента регрессии. Выступая показателем силы связи, коэффициент регрессии на первый взгляд может быть использован как измеритель ее тесноты.

Из уравнений и видно, что во втором случае результат изменяется сильнее с ростом фактора на единицу – эта величина в 10 раз больше, чем в первом случае.

Однако вывод о более сильном вли­янии фактора на результат преждевремен.

Величина коэффи­циента регрессии зависит от единиц измерения переменных, от размерности признаков. Если предположить, что выражен в центнерах и , а фактор по экономическому содержанию совпадает с фактором , но выражен в тоннах, то eсть , то понят­но, что по данным обоих уравнений , а разные значения коэффициентов регрессии обусловлены разными единицами из­мерения одного и того же фактора. Кроме того, коэффициенты регрессии – величины именованные, и потому несравнимы для разных признаков. Так, коэффициент регрессии по модели при­были предприятия от состава выпускаемой продукции несопос­тавим с коэффициентом регрессии прибыли предприятия от зат­рат на рекламу.

Линейный коэффициент корреляции как измеритель тесно­ты линейной связи признаков логически связан не только с ко­эффициентом регрессии , но и с коэффициентом эластичности, который является показателем силы связи, выраженным в про­центах.

При линейной связи признаков и средний коэффици­ент эластичности в целом по совокупности определяется как:

, (14)

Формула среднего коэффици­ента эластичности по построению близка к формуле линейного коэффициента корреляции

, (12)

Как и линейный коэффициент корреляции, коэффициент эластичности сравним по разным признакам. Если , а , то можно заключить, что фактор в большей мере влияет на резуль­тат , чем фактор , ибо с ростом на 1 % возрастает на 0,8 %, а с ростом на 1 % – только на 0,2 %.

Несмотря на схожесть этих показателей, измерителем тесно­ты связи выступает линейный коэффициент корреляции , а коэффициент регрессии и коэффициент эластичности – показатели силы связи.

Коэффициент регрессии является абсолютной мерой, так как имеет единицы измерения, присущие изучаемым признакам и , а коэффициент эластичности – от­носительным показателем силы связи, потому что выражен в про­центах.

Несмотря на всю важность измерителя тесноты связи, в эконо­метрике больший практический интерес приобретает коэффици­ент детерминации , так как он дает относительную меру влияния фактора на результат, фиксируя одновременно и роль ошибок, то есть случайных составляющих в формировании моделируемой пере­менной. Чем ближе коэффициент детерминации к 1, тем в боль­шей степени уравнение регрессии пригодно для прогнозирования.