Тема №2 Линейная регрессия и корреляция в эконометрических исследованиях

Вопросы:

1.Оценка параметров линейной регрессии методом наименьших квадратов

2. Расчет параметров линейной регрессии

3.Экономический смысл и содержание показателей тесноты связи в линейных моделях

1.Оценка параметров линейной регрессии методом наименьших квадратов

Линейная регрессия находит широкое применение в экономет­рике ввиду четкой экономической интерпретации ее параметров.

Линейная регрессия сводится к нахождению уравнения вида

или (1)

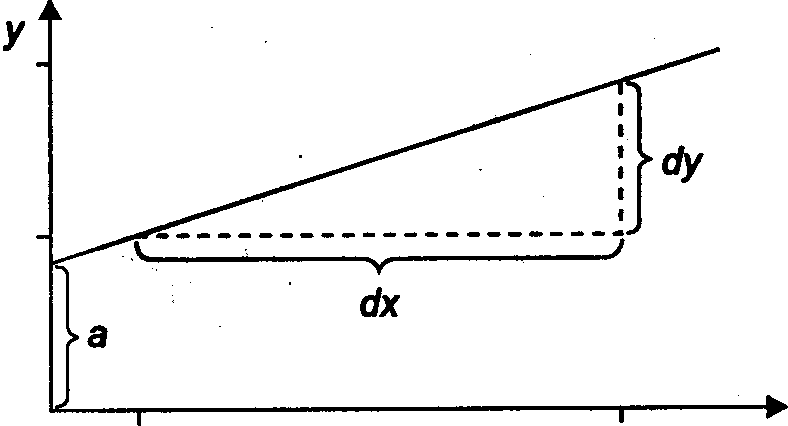
Уравнение вида позволяет по заданным значени­ям фактора иметь теоретические значения результативного признака подстановкой в него фактических значений фактора (рис. 1).

О х

Рис. 1– Графическая оценка параметров линейной регрессии

Построение линейной регрессии сводится к оценке ее пара­метров – и .

Оценки параметров линейной регрессии могут быть найдены разными методами. Можно обратиться к полю корреляции и, выбрав на графике две точки, провести через них прямую линию (см. рис. 1), затем по графику найти значения параметров.

Параметр определим как точку пересечения линии регрессии с осью оу, а параметр оценим исходя из угла наклона линии регрессии как

, (2)

где – приращение результата ;

– приращение фактора .

Классический подход к оцениванию параметров линейной регрессии основан на методе наименьших квадратов (МНК).

Метод наименьших квадратов позволяет получить такие оценки параметров и , при которых сумма квадратов отклоне­ний фактических значений результативного признака от рас­четных (теоретических) минимальна:

, (2)

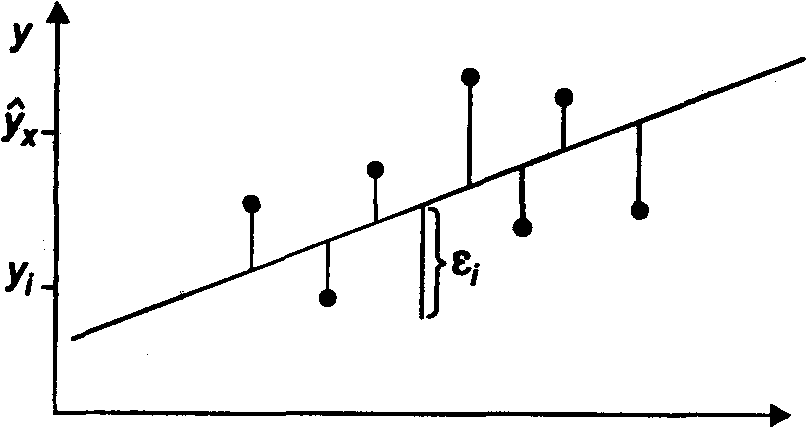
Иными словами, из всего множества линий линия регрессии на графике выбирается так, чтобы сумма квадратов расстояний по вертикали между точками и этой линией была бы минималь­ной (рис. 2);

следовательно,

, (3)

0 х

Рис. 2–  Линия регрессии с минимальной дисперсией остатков

Для того чтобы найти минимум функции (2), надо вычис­лить частные производные по каждому из параметров и , и при­равнять их к нулю.

Обозначим через , тогда:

;

; (4)

;

Преобразуя формулу (4), получим следующую систему нор­мальных уравнений для оценки параметров и :

, (5)

Решая систему нормальных уравнений (5) либо методом последовательного исключения переменных, либо методом оп­ределителей, найдем искомые оценки параметров и .

Можно воспользоваться следующими формулами для и :

, (6)

Формула (6) получена из первого уравнения системы (5), если все его члены разделить на ;

, (7)

где – ковариация признаков;

– дисперсия признака .

Поскольку

, (8)

, (9)

получим сле­дующую формулу расчета оценки параметра :

, (10)

Формула (10) получается также при решении системы (5) ме­тодом определителей, если все элементы расчета разделить на .

Параметр называется коэффициентом регрессии. Его вели­чина показывает среднее изменение результата с изменением фактора на одну единицу.

Так, если функция издержек ( , тыс. руб.) выражается как ( – количество единиц про­дукции), то, следовательно, с увеличением объема продукции на одну единицу издержки производства возрастают в среднем на 2 тыс. руб., то есть дополнительный прирост продукции на одну единицу потребует увеличения затрат в среднем на 2 тыс. руб.

Знак при коэффициенте регрессии показывает направление связи: – при > 0 – связь прямая;

– при < 0 – связь обратная.

Возможность четкой экономической интерпретации коэф­фициента регрессии сделала линейное уравнение регрессии дос­таточно распространенным в эконометрических исследованиях.

Формально – значение у при . Если признак– фактор не имеет и не может иметь нулевого значения, то трактовка сво­бодного члена не имеет смысла. Параметр может не иметь экономического содержания. Попытки экономически интерпре­тировать параметр могут привести к абсурду, особенно при < 0.

Интерпретировать можно лишь знак при параметре . Если > 0, то относительное изменение результата происходит мед­леннее, чем изменение фактора. Иными словами, вариация ре­зультата меньше вариации фактора – коэффициент вариации по фактору выше коэффициента вариации для результата : > .

Для доказательства данного положения сравним относи­тельные изменения фактора и результата :

или ; ; , (11)