25. Исследование сходимости несобственных интегралов.

Для существования определенного интеграла необходимо, чтобы промежуток интегрирования был конечен, а подынтегральная функция ограничена на нем. При решении задач встречаются случаи, когда одно или оба из этих условий не выполняются, т. е. когда промежуток интегрирования бесконечен или подынтегральная функция не ограничена. Такие интегралы называются несобственными. Различают несобственные интегралы 1-го и 2-го рода в зависимости от того, имеем ли мы дело с бесконечностью промежутка интегрирования или с неограниченностью подынтегральной функции.

Начнем со случая, когда промежутком интегрирования является луч[a, +∞) . Предположим, что функция y=f(x) интегрируема на каждой конечной части луча, т. е. что для любого c>a существует интеграл . За значение интеграла естественно принять предел функции I(c), когда с стремится к +∞, т. е. когда промежуток интегрирования стремится заполнить весь луч [a, +∞)

Может, однако, случиться, что этот предел не существует. Поэтому будем различать два случая:

а) Если предел существует и конечен, то несобственный интеграл называют сходящимся, а значение этого предела — значением несобственного интеграла. В этом случае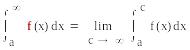 (1)

б) Если предел в правой части равенства (1) не существует, говорят, что несобственный интеграл расходится.

При аналогичных предположениях относительно функции можно рассмотреть случай, когда верхний предел фиксирован, а нижний предел стремится к -∞

(2)Если предел, стоящий в правой части равенства (2), конечен, то несобственный интеграл

называют сходящимся, в противном случае его называют расходящимся.

26 Основные определения и понятия о фмп

При рассмотрении ФМП ограничимся подробным описанием функций двух переменных, т.к. все полученные результаты будут справедливы для функций произвольного числа переменных.

Определение: Если каждой паре независимых друг от друга чисел (х, у) из некоторого множества по какому - либо правилу ставится в соответствие одно или несколько значений переменной z, то переменная z называется функцией двух переменных.

Определение: Областью определения функции z называется совокупность пар (х, у), при которых функция z существует.

Окрестность т. Мо

- окрестность т. Мо – открытый шар( без ограничивающей его сферы) с центром в т. Мо и радиусом r.

N-мерный шаг с центром в т. Мо и радиусом r – это множество точек пр-ва Rn, которые находятся от т.Мо на расстоянии ≤ r

Неравенство, задающее n-мерный шаг



N=1:

N=2: круг с центров в т. Мо и радиусом r

N=3: шар с центров в т. Мо и радиусом r

27 Предел фмп в точке. Свойство фмп, имеющих предел в точке

Пусть функция z = f(x;y) определена в некоторой окрестности точки M₀(x₀;y₀), кроме, самой этой точки. Число А называется пределом функции z = f(x;y) при x -> x₀и при y -> y₀(или при M(x;y) -> M₀(x₀;y₀)), если для любого ε > 0 существует δ > 0 такое, что для всех х != х₀и y != y₀ и удовл. неравенству выполняется неравенство: |f(x;y) – A| < ε. Записывают: