22.Вычисление объемов тел с помощью определенного интеграла

1) Вычисление объема по заданной площади поперечного сечения. Рассмотрим некоторое тело T. Возьмем произвольное x и проведем плоскость, перпендикулярно оси Ox. В сечении получим плоскую фигуру. Предположим, что площадь этой фигуры S(x) нам известна и функция S(x) непрерывна на сегменте [a, b]. Найдем объем этого тела T. Разобьем сегмент [a, b] произвольно на n частей

.

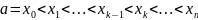Через каждую точку деления проведем плоскость перпендикулярную оси Ox. При этом все тело T разобьется на определенные элементарные слои, вычислим приближенно объем одного слоя. Для этого выберем произвольную точку 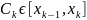и проведем через эту точку плоскость, перпендикулярную оси Ox. Площадь плоской фигуры, полученной в сечении, равна 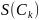. Заменим теперь элементарный слой цилиндром с основанием, площадь которого есть , и высотой . Тогда 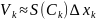и, следовательно,

Полученная сумма есть, очевидно, интегральная сумма, составленная для непрерывной функции S(x), Следовательно эта интегральная сумма имеет конечный предел при 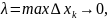независящий ни от способа разбиения [a,b] ни от выбора точек 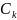. Итак, окончательно

2) Объем тела вращения.

23.Несобственный интеграл I рода. Вычисление, главное значение

Пусть функция f(x) непрерывна на промежутке [a,-∞). Если существует конечный предел 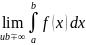, то его называют несобственным интегралом первого рода и обозначают

Таким образом, по определению:

В этом случае говорят,что несобственный интеграл 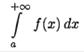сходится. Если же указанный предел не существует или он бесконечен, то говорят, что интеграл расходится.

Аналогично определяется несобственный интеграл на промежутке (-∞;b].

Несобственный интеграл с двумя бесконечными пределами определяется формулой:

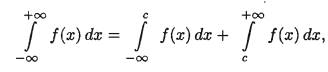
Где с- произвольное число. В этом случае интеграл слева сходится

24.Несобственный интеграл II рода. Вычисление, главное значение

Пусть функция f(x) непрерывна на промежутке [a;b) и имеет бесконечный разрыв при x = b. Если существует конечный предел , то его называют несобственным интегралом второго рода и обозначают .

Таким образом, по определению,

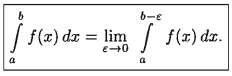
Если предел в правой части существует, то несобственный интеграл сходится. Если же указанный предел не существует или бесконечен, то говорят, что интеграл расходится.

Аналогично, если функция f(x) терпит бесконечный разрыв в точке x = a, то полагают

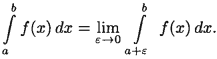
Если функция f(x) терпит разрыв во внутренней точке с отрезка [a;b], то несобственный интеграл второго рода определяется формулой.

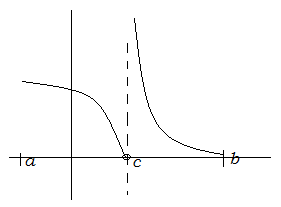
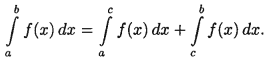
В этом случае интеграл слева называют сходящимся, если оба несобственных интеграла, стоящих справа, сходятся.

В случае, когда f(x)>0, несобственный интеграл второго рода (разрыв в точке x=b) можно истолковать геометрически как площадь бесконечно высокой криволинейной трапеции