
- •Понятие комплексного числа. Алгебр-ая форма представления. Операции над комплексными числами в алгебр. Форме
- •Тригонометрическая форма представления комплексного числа. Умножение и деление чисел.
- •Формула Муавра извлечения корня степени n (n ϵ n) и возведения в целую степень
- •4 Показательная форма комплексного числа. Операции над числами, записанными в показательной форме.
- •5 Многочлен в комплексной области. Основные теоремы о мн-ах.
- •6. Первообразная и неопределенный интеграл. Простейшие свойства неопределенного интеграла.
- •Основные методы интегрирования. Неопределенное (табличное) интегрирование. Таблица основных неопределенных интегралов.
- •2.Метод замены переменной–основан на использовании формулы
- •Интегрирование с подстановкой в неопределенном интеграле.
- •Интегрирование по частям. Классы функций, интегрируемых по частям.
- •10. Алгоритм интегрирования рациональной функции. Интегрирование простейших дробей. Интегрирование дробей I и II типов
- •11. Теорема о разложении правильной рациональной дроби в сумму простейших дробей. Интегрирование дробей III и IV типов.
- •12. Методы интегрирования тригонометрических выражений
- •13. Интегрирование иррациональных выражений
- •14.Задачи, приводящие к понятию определенного интеграла. Определение интеграла Римана.
- •15.Геометрический и механический смысл определенного интеграла. Необходимые условия интегрируемости функции на отрезке [a;b]. Достаточные условия интегрируемости.
- •Необходимое условие интегрируемости функции на отрезке [a;b].
- •17. Интеграл с переменным верхним пределом и его свойства
- •18.Основные теоремы интегрального исчисления.
- •19 Основные методы вычисления определенного интеграла
- •1 Метод подстановки (Теорема)
- •2 Интегрирование по частям.
- •3 Симметрия подинтегральной функции
- •21.Определение длины плоской кривой. Вычисление длины кривой.
- •22.Вычисление объемов тел с помощью определенного интеграла
- •23.Несобственный интеграл I рода. Вычисление, главное значение
- •24.Несобственный интеграл II рода. Вычисление, главное значение
- •25. Исследование сходимости несобственных интегралов.
- •26 Основные определения и понятия о фмп
- •27 Предел фмп в точке. Свойство фмп, имеющих предел в точке
- •28 Непрерывность фмп в точке и на компакте
- •29 Частные и полное приращения фмп. Частные производные и
- •30 Полный дифференциал фмп. Использование в приближенных
- •31 Касательная плоскость и нормаль к поверхности
- •32 Производная по направлению. Градиент.
- •34 Второй дифференциал фмп как квадратичная форма от
- •35 Локальные экстремумы фмп. Необходимые условия экстремума.
- •36.Условные экстремумы фмп. Метод подстановки и метод Лагранжа.
- •37 Нахождение наибольшего и наименьшего значения функции в
- •38. Ду I порядка. Основные определения, понятия и теоремы
- •39. Точные ду. Критерий точного ду. Методы интегрирования
- •40. Уравнения с раздел-ся перем-ми. Однородные ду 1 порядка
- •41.Линейные ду первого порядка. Ду Бернули
- •42 Ду высшего порядка. Основные определения, понятия, теоремы
- •43 Ду высшего порядка, допускающие понижения порядка
- •44 Лоду высшего порядка. Свойства решений лоду. Теорема о
- •45. Линейная зависимость и независимость систем функций на
- •46. Лоду с постоянными коэффициентами. Метод Эйлера. Случаи простых действительных корней и кратных действительных корней характеристического уравнения
- •47. Лоду с постоянными коэффициентами. Метод Эйлера. Случай комплексно-сопряженных корней характеристического уравнения.
- •48. Лоду высшего порядка. Cтруктурa общего решения. Метод Лагранжа.
- •49. Лнду высшего порядка со специальной правой частью
- •50. Фигура и ее мера. Определение интеграла по фигуре. Частные случаи таких интегралов
- •51. Общие свойства интегралов по фигуре. Вычисление кри-1
- •52.Определение и вычисление кри-2. Механический смысл кри-2.
- •Скалярная форма кри-2
- •53.Двойной интеграл геом. И мех. Смысл. Вычисление
- •54.Тройной интеграл. Геометрический и механический смысл. Вычисление
- •Замена переменных в тройном интеграле.
Интегрирование с подстановкой в неопределенном интеграле.
Метод интегрирования подстановкой заключается во введении новой пере мен ной интегрирования (т. е. подстановки). При этом заданный интеграл при водится к новому интегралу, который является табличным или к нему сводящимся (в случае «удачной» подстановки). Пусть требуется вычислить интеграл ∫ f(x) dx. Сделаем подстановку х = φ(t), где φ(t) - функция, имеющая непрерывную производную.
Тогда dx =φ'(t) dt и на основании свойства инвариантности формулы интегрирования неопределенного интеграла получаем формулу интегрирования подстановкой,
∫f(x)dx=∫f(
(t)) φʹ(t)dt.
Эта
формула также называется формулой
замены переменных в неопределенном
интеграле.
φʹ(t)dt.
Эта
формула также называется формулой
замены переменных в неопределенном
интеграле.
После нахождения интеграла правой части этого равенства следует перейти от новой переменной интегрирования t назад к переменной х.
Иногда целесообразно подбирать подстановку в виде t = φ(х), тогда
∫f(φ(x)∙φʹ(x)dx=∫f(t)dt, где t=φ(x).
Другими словами формулу можно применять справа налево.
Интегрирование по частям. Классы функций, интегрируемых по частям.
Пусть u=u(x), v=v(x), тогда

док-во!
 =uv+c;
d(uv)=(uv
=uv+c;
d(uv)=(uv =
= =
= +
+ ;
=
-
;
=
- =uv-
=uv- .
1. Ф-ла интегрирования по частям применяется
для вычисления следующих интегралов:
1)
.
1. Ф-ла интегрирования по частям применяется
для вычисления следующих интегралов:
1)
 ;
2)
;
2)
 dx;
dx;
 -многочлен
степени n;
k
-многочлен
степени n;
k k-некоторое
действительное число;
=u(x);
k-некоторое
действительное число;
=u(x); dx=dv.
2. Ф-ла интегрирования по частям применяется
для вычисления интегралов
dx=dv.
2. Ф-ла интегрирования по частям применяется
для вычисления интегралов
 dx
при вычислении этих интегралов
dx
при вычислении этих интегралов
 =u;
=u;
 =dv.
3. Ф-ла интегрирования по частям применяется
для вычисления интегралов вида
=dv.
3. Ф-ла интегрирования по частям применяется
для вычисления интегралов вида
 dx
такие интегралы наз сводящимися
сами к себе;
dx
такие интегралы наз сводящимися
сами к себе;
 =dv;
=dv;
 =u
=u
10. Алгоритм интегрирования рациональной функции. Интегрирование простейших дробей. Интегрирование дробей I и II типов
Дробно-рациональная
ф-ция
называется ф-ция равная отношению двух
многочленов: f(x)
=
 где Pm(x)
– многочлен степени m,
а Qn(x)
многочлен степени n.
где Pm(x)
– многочлен степени m,
а Qn(x)
многочлен степени n.
Всякую неправильную рац. Дробь можно, путем деления числителя на знаменатель, представить в виде суммы многочлена и правильной рац.дроби.
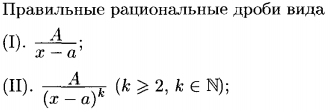
Простейшие рац. Дроби I и II типа.
Всякую правильную рац.дробь знаменатель которой разложен на множители, можно представить в виде следующей сумму простейших дробей (ПРИМЕР):
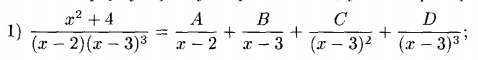
Интегрирование
простейших рац.дробей (I
и II):
I.
 =
A*ln|x-a|+C
II.
=
A*ln|x-a|+C
II.
11. Теорема о разложении правильной рациональной дроби в сумму простейших дробей. Интегрирование дробей III и IV типов.
Интегрирование простейших рац. дробей
III.

IV.
12. Методы интегрирования тригонометрических выражений
Табличное интегрирование


Универсальная подстановка

Интегрирование с помощью понижения степени


Интегрирование по частям

Использование тригонометрических преобразований.
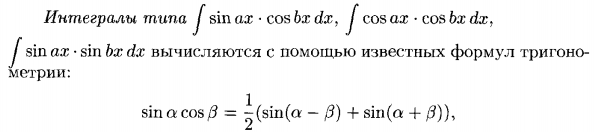
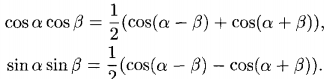
13. Интегрирование иррациональных выражений
Общий принцип интегрирования иррациональных выражений заключается в замене переменной, позволяющей избавиться от корней в подынтегральном выражении. Для некоторых классов функций эта цель достигается с помощью стандартных замен.
Интегралы
вида
 ,
где
,
где  -
рациональная функция своих аргументов,
вычисляются заменой
-
рациональная функция своих аргументов,
вычисляются заменой
 .
.
Интегралы
вида  вычисляются
заменой
вычисляются
заменой  или
или 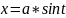 .
.
Интегралы
вида  вычисляются
заменой
вычисляются
заменой  или
или
 .
.
Интегралы
вида  вычисляются заменой
вычисляются заменой  или
или .
.
