1. Понятие комплексного числа. Алгебр-ая форма представления. Операции над комплексными числами в алгебр. Форме

Комплексным числом Z называется выражение вида: z = x+iy (АЛГЕБРАИЧЕСКАЯ ФОРМА КОМЛ,ЧИСЛА), где х и y – действительные числа, а i – мнимая еденица, i² = -1;

Если х = 0, то число 0 + iy = iy называется числом мнимым.

Если y = 0, то число x +i0 = x отождествляется с действительным числом х, а это означает, что множество R всех действительных чисел является подмножеством множества С всех комплексных чисел. Т.е.:

Число х называется действительной частью комплексного числа z и обозначается x = Rez, а y мнимой частью z, y = Imz

Комплексное число можно записать в виде:

z = r (cosφ – isinφ) (тригонометрическая форма записи)

Действия над комплексными числами:

Сумма: Суммой двух К.чисел z₁ = x₁ + iy₁ и z₂ = x₂ + iy₂ наз-ся К.число, определяемое равенством

z₁ + z₂ = (x₁ + x₂) + i(y₁ + y₂)

Сложение обладает переместительным и сочетательными св-вами:

z₁ + z_{2 =} z₂ + z₁

(z₁ + z₂) + z₃ = z₁ + (z₂ + z₃)

Разность: z = z₁ – z₂ если z + z₂ = z₁

Если z₁ = x₁ + iy₁, z₂ = x₂ + iy₂, тогда:

z = z₁ – z₂ = (x₁ – x₂) + i(y₁ – y₂)

Умножение:

z = z₁z₂ = (x₁x₂ – y₁y₂) + i(x₁y₂ + y₁x₂)

Деление:

2. Тригонометрическая форма представления комплексного числа. Умножение и деление чисел.

Комплексное число можно записать в виде:

z = r (cosφ – isinφ) (тригонометрическая форма записи)

Т-ма: Пусть z_i = |z_i|(cos _i + sin _i*i); тогда:

z₁*z₂ = |z₁|*|z₂|(cos( ₁+ ₂) +i* sin( ₁+ ₂));

z₁/z₂ = *(cos( ₁ – ₂)+i* sin( ₁- ₂)).

В частности, 1/z₂ = z₂^-1 = 1/|z₂| *(cos(-Fi₂) + i*sin(-Fi₂)).

Модуль r = | z | определяется по формуле:

r = | z | =

a φ удовлетворяет условиям:

2. Формула Муавра извлечения корня степени n (n ϵ n) и возведения в целую степень

Формула Муавра возведения в целую степень и извлечение корня нат.степени из z != 0

Корнем n-й степени из комплексного числа z называется комлексное число ω, удовлетворяющее равенству

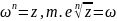
Если положить z = r(cos + i sin , a

z = = r(cos + i sin =

(арифметический корень)

Поэтому равенство примет вид:

4 Показательная форма комплексного числа. Операции над числами, записанными в показательной форме.

Z = r

– Формула Эйлера (показательная, экспоненциальная форма записи)

Модуль r = | z | определяется по формуле:

r = | z | =

ОПЕРАЦИИ:

5 Многочлен в комплексной области. Основные теоремы о мн-ах.

Опр: Выражение вида C_nzⁿ+C_nz^n-1+….+C₁z+C₀ = P_n(z), где C_n ,..,C₀ прин. C(перечеркнутое вертикально), C_n ≠0,z = x+i*y – комплекс.перемен. – называется комплексным многосленом степени n. Число z – корень P_n(z), если P_n(z₀) = 0. Z₀ – простой корен многочлена P_n(z),если P_n(z₀) = 0, но P’_n(z₀) ≠0. Число z₀ – корень кратности k (>=1), если P_n(z₀) = 0, P’_n(z₀) = 0,..,P^(n-1)_n(z₀) = 0,но P⁽ⁿ⁾_n(z₀) ≠0; Основная теорема алгебры(Гаусса): Любой многочлен P_n(z),n >=1,имеет хотя бы один корень,действительный или комплексный. Следствие(т-ма Гаусса): Любой многочлен P_n(z) степени n>=1 имеет ровно n корней, считая любой из низ столько раз,какова его кратность.

Док-во: Пусть дан любой P_n(z), n>=1.По основной т-ме алгебры сущ.его корень z₀.Тогда по т-ме Безу: если z₀ – корень P_n(z),то P_n(z) = (z-z₀)P_n-1(z). Далее по осн.теореме алгебры сущ.корень z₁ мн-ва P_n-1(z) => по т-ме Безу P_n-1(z) = (z-z₁)P_n-2(z); Проделав n аналогичных шагов, приходим к оконч. результату.Сущ. ровно n корней мн-ва P_n(z), при этом P_n(z) = C_n(z-z₀)(z-z₁)….(z-z_n-1), ч.т.д. Рассм. многочлен Q_n(x) = a_nxⁿ+a_n-1x^n-1+…+a₁x+a₀, где a_n,a_n-1,….,a₁,a₀ прин. R(!) Известен след.результат, елси многочлен Q_n(x) имеет корень z₁ = a+b*i, b ≠0, то он имеет и комплекно сопряженный корень = a-b*i. Множители (z-z₁)(z- ) = (z-(a+b*i))*(z-(a-b*i))=(z-a)²+b²; Если z=x прин.R,то: (x-z₁)(x- ) = (x-a)²+b² >0; Вывод: для многочленов Q_n(x) с действительным коэф.справедливо след.разложение на многочлены: Q_n(x) = a_n(x-a)^α+…+(x-b)^β(x²+px+q)^γ+…+(x²+rx+s)^δ, где a,b – действительные корни Q_n(x),кратные α…β; x²+px+q,…,x²+rx+s – квадратич.трехчлены с D<0, a_i+b_i и a_i-b_i кратны γ и δ.