3.2.1 Транспортирование частиц шлама по стволу вертикальных и наклонных скважин

В восходящем потоке жидкости частицы шлама, имея плотность ρ_п больше плотности промывочной жидкости ρ_ж , стремяться опускаться относительно жидкости (рисунок 3.11). Вынос шлама будет обеспечен, если средняя скорость восходящего потока будет больше скорости оседания

U_ж > U_ос (3.25)

отсюда, необходимый расход

Q ≥ 1,15 U_ос S_кп (3.26)

Таким образом, определение расхода сводится к определению скорости оседания частиц в восходящем потоке.

Анализ размерностей позволяет установить, что процесс оседания твердой частицы в потоке жидкости зависит от режима обтекания частицы жидкостью, режима течения самой жидкости, параметра Архимеда, формы твердой частицы, объемного содержания этих частиц и соотношения размеров частицы и канала.

Для жидкости Бингама имеем

Rе_ос = f (Re, Ar, He, ψ, φ, d/D_r) (3.27)

где Rе_ос = U_осdρ_ж/η;

;

He = τ₀D_r²ρ/η² ;

,

φ - объемное содержание выбуренной породы в потоке;

d – характерный размер твердой части;

D_r – гидравлический диаметр кольцевоо пространства;

ψ - коэффициент формы частиц шлама. Его можно оценивать как отношение площади поверхности частицы к площади поверхности равновеликого по объему шара.

Расчет скорости оседания одиночной частицы в восходящем потоке ньютоновской жидкости. Пусть в восходящем потоке имеется одиночная частица шарообразной формы, которая движется относительно жидкости со скоростью U_ос.

На частицу действует сила веса сила Архимеда

(3.28)

и сила, обусловленная скоростным напором жидкости F_р (рисунок 3.11).

Скоростной напор жидкости в т.А, согласно уравнению Бернулли, будет равен

Р_А = 0,5ρ_ж U_ос² (3.29)

Сила, с которой жидкость воздействует на частицу

F_р = Р_АS С_f (3.30)

где S = πd²/4 – площадь проекции частицы на плоскость, нормальную к вектору U_ос;

С_f - коэффициент сопроптивления, учитывающий неравномерность скоростного напора жидкости по поверхности частицы. В условиях установившегося движения (U_ос = const) сумма всех действующих сил будет равна нулю.

G - F_ar - F_р=0 (3.31)

Подставляя (3.28) - (3.30) в (3.31), получим

(3.32)

Формула (3.32) носит название уравнение Риттингера. Величина коэффициента сопротивления С_f зависит от свойств жидкости и режима обтекания. Экспериментальная зависимость С_f от (Rе) для шарообразной частицы в ньютоновской жидкости показана на рисунок 3.12.

Рисунок 3.12 - Зависимость коэффициента сопротивления среды С_f от режима обтекания шарообразных частиц ньютоновской жидкостью

При Rе_ос<2 имеет место ламинарное обтекание частицы (рисунок 3.13 а) и

С_f = 24\Rе_ос (3.33)

Рисунок 3.13 - Схема ламинарного (а) и турбулентного (б) обтекания твердой частицы жидкостью

Подставляя (3.33) в (3.32), получим уравнение Стокса для скорости оседания шарообразной частицы в ньютоновской жидкости при ламинарном обтекании.

U_ос= ∆ρgd²⁄18μ (3.34)

При Rе>10³ наблюдается турбулентное обтекание C_f ≈ 0,44 и формула Риттингера получает вид

(3.35)

Расчеты по формулам (3.34) и (3.35) неудобны тем, что для выбора той или иной формулы нужно знать режим обтекания, а для этого необходимо знать скорости оседания.

Этого недостатка лишена аппроксимационная формула, предложенная О.М. Тодесом и Р.Б. Розенбергом

(3.36)

Для мелких частиц, у которых , обтекание ламинарное и формула (3.36) переходит в формулу Стокса. Для крупных частиц ( ), оседающих с турбулентным обтеканием, формула (3.36) переходит в формулу Риттингера.

Вынос твердых частиц потоком вязкопластичной жидкости Бингама

Картина движения твердой частицы в восходящем потоке ВПЖ значительно сложнее. При ламинарном (структурном) режиме течения ВЖП в кольцевом пространстве образуется ядро течения, где скорость практически постоянна (рисунок 3.14).

Рискнок 3.14 - Профиль скорости восходящего потока ВПЖ в кольцевом пространстве

В ядре течения, где жидкость движется с неразрушенной структурой, твердым частицам для оседания необходимо преодолеть прочность структуры. Поэтому мелкие частицы размером

(3.37)

практически не оседают, у них U_ос ≈ 0. В градиентных зонах, где структура раствора в той или иной мере разрушена, все частицы оседают. Это обстоятельство затрудняет строгое аналитическое решение задачи определения скорости оседания.

Силу сопротивления частиц, оседающих с ламинарным обтеканием в ядре течения, найдем методом раздельного учета сил вязкости F₂ и сил пластичности F_τ0.

F_p = F_η+F_τ (3.38)

При ламинарном обтекании силу вязкого трения найдем из формулы Стокса

F_η = 3πdηU_ос (3.39)

Силу, обусловленную динамическим напряжением сдвига, найдем из выражения

F_τ = τ₀f = τ₀πd² (3.40)

Подставляя (3.39), (3.40) и (3.28) в (3.31) получим

(3.40 а)

или (3.40 б)

По аналогии с ньютоновской жидкостью обобщим формулу (3.40 б) и на область турбулентного обтекания

(3.41)

При Аr < 6Не, т.е. при , считается, что U_ос ≈ 0.

3) Расчет выноса частиц шлама потоком степенной жидкости (Оствальда де Вааля).

Уолкер и Мейз предлагают следующую методику.

Определяется среднее напряжение сдвига на поверхности падающей частицы

(3.42)

где d- диаметр частицы в м.

По реограмме находится градиент скорости на поверхности частицы j .

Он сравнивается с критическим градиентом скорости, определяемым из выражения

(3.43)

Если j < j_кр- обтекание частицы ламинарное . Скорость оседания частицы при этом предлагается находить из выражения

(3.44)

При j > j кр – обтекание частицы жидкостью турбулентное. В этом случае

(3.45)

Пример. Определить скорость оседания твердой частицы диаметром 5 мм и плотностью ρ = 2500 кг/м^з в ламинарном потоке жидкость плотностью ρ_ж = 1200 кг/м, реограмма которой показана на рисунок 3.15.

2,5

Рисунок 3.15 - Реограмма промывочной жидкости

Реологические характеристики этой жидкости по модели Бингама – τ₀ = 5 Па, η = 0,01 Па∙с, по модели Оствальда-де Вааля- m = 0,33, к = 1,27 Па∙с^0,33.

Если жидкость считать Бингамовской, скорость оседания определяется по формуле (3.41), в которой

При расчете по методике Уолкера и Мейза имеем

По реограмме определяем j = 50 с^-1,

Критический градиент скорости

Поскольку j < j_кр, обтекание частицы ламинарное. Скорость оседания находим из уравнения (44)

В таблице 3.3 приведены расчетные скорости оседания, найденные по обеим методикам.

Таблица 3 - Расчетные скорости оседания частиц шлама, м/с

Диаметр частиц , мм	1	5	10
По методике Уодкера и Мейза	0,006	0,1	0,34
По уравнению (17)	0,0	0,096	0,38

Из приведенных данных следует, что обе методики дают практически одинаковые результаты. Зависимости (3.41) - (3.44) справедливы при ламинарном течении ВПЖ в кольцевом пространстве. Если же жидкость движется в турбулентном режиме, в котором структура раствора разрушена, скорости оседания рассчитываются по формуле Риттингера

Форма частиц бурового шлама отличается от сферы. Чаще всего это пластинки, пирамидки или частицы неправильной формы. Скорость оседания твердых частиц, форма которых отличается от сферы в покоящейся жидкости всегда меньше скорости оседания сферических частиц равного объема, поскольку частицы неправильной формы занимают положение, в котором сила сопротивления максимальна.

В движущемся потоке из-за градиента скорости по сечению канала частицы все время вращаются, это в какой-то мере уменьшает влияние формы частиц, и, по нашему мнению, можно считать скорость оседания частиц шлама как сферических частиц.

Очевидно, что при расчете необходимого для транспортирования шлама расхода в зависимости (3.26) следует подставлять скорость оседания наиболее крупных частиц и максимальную площадь кольцевого пространства. Естественно, размер частиц шлама зависит от свойств разбуреваемых пород, режима бурения, типоразмера долота.

Размер наиболее крупных частиц, образующихся при бурении шарошечными долотами, может быть найден из следующих зависимостей

; (3.46)

(3.47)

где t - максимальный шаг зубьев;

b – ширина зуба;

l - высота зуба;

D_д - диаметр долота, м.

3.3 Расход, обеспечивающий заданный режим течения в кольцевом пространстве

Как указывалось выше, при проходке ММП, минимальное их растепление достигается при ламинарном режиме течения в КП, а наилучший транспорт шлама в эксцентричном кольцевом пространстве - при турбулентном.

Для жидкости, описываемой уравнением Бингама критическое значение параметра Rе, при котором ламинарный режим течения переходит в ламинарный, определяется выражением

Rе_кр = 2100 + 7,3Hе^0,58 (3.48)

отсюда критическое значение расхода

(3.49)

где D_г- гидравлическоий диаметр кольцевого пространства;

Не = τ₀D_r²ρ/η² – параметр Недстрема.

При Не > 5∙10⁵

, отсюда

(3.50)

Для жидкости Оствальда-де Вааля , известны следующие диапазоны режимов течения

Rе_m < 3470-1370m- ламинарное течение (3.51)

Rе_m > 4270-1370m- турбулентное течение, в интервале между этими значениями- переходное течение,

(3.52)

отсюда

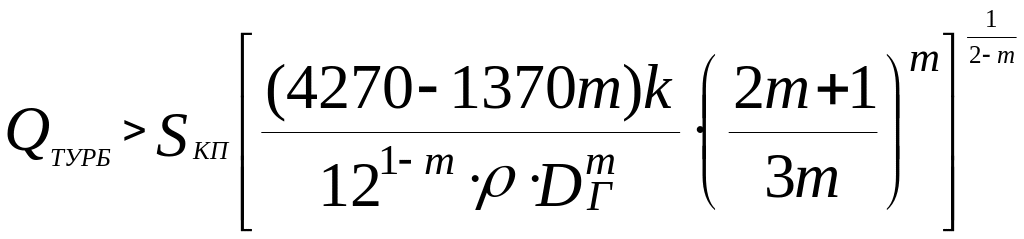
3.4 Расход жидкости, необходимый для нормальной работы гидравлического забойного двигателя

Для этого необходимо, чтобы момент, создаваемый двигателями, был больше момента, требуемого для вращения долота М_д при заданной осевой нагрузке G_д.

Момент, создаваемый турбиной турбобура, пропорционален плотности и квадрату расхода жидкости, и может быть найден из выражения

(3.54)

где М_с, Q_c, ρ_c- момент турбины при расходе Q_с жидкости плотностью ρ_с, полученный при стендовых испытаниях турбины (приводятся в справочниках). Однако, не весь момент, создаваемый турбиной, доходит до долота, часть его теряется в подшипниках турбобура, в основном в осевой опоре. Ориентировочно можно считать, что в резинометаллической осевой опоре теряется до 30%, а в осевой шаровой опоре- до 10% момента турбины. Следовательно, для нормальной работы турбобура необходимо иметь

где к - коэффициент, учитывающий потери момента в осевой опоре турбобура. к ≈ 0,3 при резинометаллической и к ≈ 0,1 при шаровой опоре турбобура. Отсюда необходимый расход промывочной жидкости, обеспечивающий нормальную работу турбобура

(3.55)

М_д=М₀+М_уд∙G_д (3.56)

где М₀ - момент на долоте при нулевой осевой нагрузке (за счет трения о стенки скважины и о жидкость);

М_уд - удельный момент на долоте, зависящий от механических свойств разбуреваемых долот и типоразмера долота;

G_д- нагрузка на долоте, с учетом (3.56) выражение (3.55) принимает вид

(3.57)

где G – нагрузка на долото.

У гидравлических двигателей объемного типа создаваемый момент пропорционален расходу в первой степени. Необходимый для их нормальной работы расход

(3.58)

3.5 Расход, при котором содержание шлама в восходящем потоке жидкости в КП не превышает заданной величины

Практика бурения показала, что содержание шлама в потоке жидкости в КП не должна превышать 3-5%. В противном случае увеличивается вероятность налипания выбуренной породы на элементы бурильной колонны, (образование сальников), что может привести к затяжкам и прихватам.

Объемное содержание шлама в КП определяется выражением

(3.59)

где Q_шл = V_м ∙πD_д²/4 - объемный расход выбуреваемой породы;

V_м - механическая скорость проходки;

S_кп - площадь кольцевого пространства;

U_ж,U_ос - соответственно, скорость восходящего потока жидкости и скорость оседания частиц шлама, U_шл = U_ж - U_ос.

Из (3.59) получим необходимый расход промывочной жидкости, при котором содержание шлама в восходящем потоке жидкости в КП не будет больше критического

(3.60)

4 Расчет потерь давления при течении бурового раствора в трубах и кольцевом пространстве

4.1 Рассмотрим данный вопрос с помощью Пи – теоремы

Для вязкой (ньютоновской) жидкости, движущейся в ламинарном режиме, перепад давления на единицу длины канала ∆Р/l , очевидно, будет зависит от вязкости жидкости и скорости течения U и диаметра канала. Плотность жидкости ρ и шероховатости стенок Ɛ ,при ламинарном течении не оказывают влияния.

(4.1)

Выбрав в качестве основных величин 𝛍, U, d (их размерности независимы), получим один безразмерный параметр

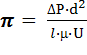
Следовательно, размерное соотношение (4.1) преобразуется в

(4.2)

Известно, что если функция одной величины равна нулю, то эта величина равна постоянной, т.е.

(4.3)

Из Пи – теоремы получили, что при ламинарном режиме ньтоновской жидкости перепад давления прямо пропорционален вязкости жидкости и скорости потока и обратно пропорционален квадрату размера канала.

Для ВПЖ Бингама, имеющих два реологических параметра, будем иметь

(4.4)

Выбрав в качестве основных величин , из (4.4) получим два безразмерных параметра

Величина, обратная , есть параметр Сен – Венана

Таким образом, из размерного соотношения (4.4) получим

(4.5)

т.е. перепад давления при ламинарном течении бингамовской жидкости зависит от безразмерного параметра Сен – Венана.

При ламинарном течении ППЖ, описываемой уравнением Освальда – де – Вааля, аналогично (4.1) и (4.4) запишем

f( ) = 0 (4.6)

Постоянная вязкости имеет размерность [k]= показатель нелинейности m - безразмерный.

Проведя аналогичные процедуры получим

(4.7)

Если жидкость движется в турбулентном режиме, то определяющими параметрами, кроме скорости течения и диаметра канала, будет плотность ρ жидкости и шероховатость стенок , т.е.

(4.8)

Из пяти размерных параметров можно получить два безразмерных

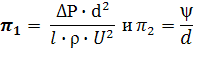
- есть относительная шероховатость, тогда

(4.9)

т.е. перепад давления при турбулентном течении прямо пропорционален плотности жидкости, квадрату скорости и обратно пропорционален диаметру канала и зависит от относительной шероховатости стенок канала.

Для эксцентричного кольцевого пространства перепад давления будет зависеть и от относительного эксцентриситета где ∆ - расстояние между центрами внешней и внутренней труб, D и d – соответственно их диаметры.