7 Закон сохранения импульса и реактивное движение.

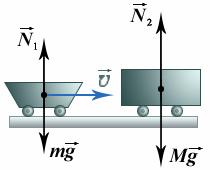
Импульсом системы тел называется сумма векторов импульсов всех тел этой системы.Силы, действующие между телами системы, называются внутренними. Силы, характеризующие воздействие тел, не входящих в систему, на тела системы, называются внешними.

На основе второго и третьего законов Ньютона может быть доказан закон сохранения импульса системы тел: в инерциальной системе отсчета импульс системы тел остается неизменным, если на систему не действуют внешние силы.

Приближенно он выполняется и в случаях, когда внешние силы конечны, а процессы, происходящие в системе, являются быстрыми и вызваны большими внутренними силами (столкновение тел, взрыв, выстрел и т. п.). Кроме того, если сумма внешних сил не равна нулю, но проекция суммы внешних сил на выбранную ось равна нулю, то сохраняется проекция импульса системы на эту ось.

, где  – скорость после сцепки вагона и вагонетки, так как сумма внешних сил равна нулю	, где m1и m2 – массы,  1 и  2– скорости осколков снаряда после его разрыва, а  – его скорость до разрыва. Силы тяжести m1  иm2  конечны, а время взаимодействия мало	, но M 1x + m 2x = (M + m)ux, т.е. M 1 = (M + m)u, так как вдоль горизонтальной оси внешние силы на вагонетку и камень не действуют

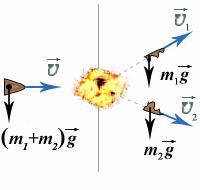
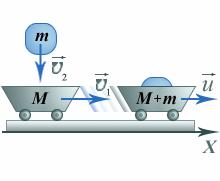
 Следует иметь в виду, что импульс тела – векторная физическая величина и его сохранение в случае равенства нулю суммы внешних сил означает выполнение векторного равенства. Например, при взаимодействии двух тел, движущихся в одной плоскости, это означает выполнение двух скалярных уравнений для проекций импульсов одновременно. Примером может служить нецентральный удар бильярдных шаров:

m_{1 1x} + m_{2 2x} = m₁u_1x + m₂u_2x

m_{1 1y} + m_{2 2y} = m₁u_1y + m₂u_2y

Реактивное движение – движение тела, возникающее при отделении от него с какой-либо скоростью некоторой его части. Если отделение частей тела происходит быстро, то для этих частей (осколки снаряда, ракета (рис. 3) и вылетающая порция продуктов сгорания топлива, тело медузы и порция выброшенной воды) выполняется закон сохранения импульса.

8. Импульс тела. Закон сохранения механической энергии.

Импульс (Количество движения) — векторная физическая величина, характеризующая меру механического движения тела. В классической механике импульс тела равен произведению массы m этой точки на её скорость v, направление импульса совпадает с направлением вектора скорости:  Закон сохранения импульса утверждает, что сумма импульсов всех тел (или частиц) замкнутой системы есть величина постоянная.. , при движении в пустом пространстве импульс сохраняется во времени, а при наличии взаимодействия скорость его изменения определяется суммой приложенных сил.  находят применение при создании современной ракетно-космической техники. Движение с помощью реактивной струи по закону сохранения импульса лежит в основе гидрореактивного двигателя. В основе движения многих морских моллюсков (осьминогов, медуз, кальмаров, каракатиц) также лежит реактивный принцип. 

Снова обратимся к простой системе тел, состоящей из земного шара и поднятого над Землей тела, например камня.    Камень падает под действием силы тяжести. Силу сопротивления воздуха учитывать не будем. Работа, совершаемая силой тяжести при перемещении камня из одной точки в другую, равна изменению (увеличению) кинетической энергии камня:

   В то же время эта работа равна уменьшению потенциальной энергии:

   Работа силы всемирного тяготения, действующей со стороны камня на Землю, практически равна нулю. Из-за большой массы Земли ее перемещением и изменениемскорости можно пренебречь. Так как в формулах (6.24) и (6.25) левые части одинаковы, то равны и правые части:

   Равенство (6.26) означает, что увеличение кинетической энергии системы равно убыли ее потенциальной энергии (или наоборот). Отсюда вытекает, что

или

   Изменение суммы кинетической и потенциальной энергий системы равно нулю.    Величину E, равную сумме кинетической и потенциальной энергий системы, называютмеханической энергией системы:

   Так как изменение полной энергии системы в рассматриваемом случае согласно уравнению (6.27) равно нулю, то энергия остается постоянной:

   Таким образом, в изолированной системе, в которой действуют консервативные силы, механическая энергия сохраняется. В этом состоит закон сохранениямеханической энергии. Энергия не создается и не уничтожается, а только превращается из одной формы в другую: из кинетической в потенциальную и наоборот.    Учитывая, что в рассматриваемом конкретном случае   и  , можно закон сохранения механической энергии записать так:

или

   Это уравнение позволяет очень просто найти скорость камня v₂ на любой высоте h₂ над землей, если известна начальная скорость v₁ камня на исходной высоте h₁.    Закон сохранения механической энергии (6.29) легко обобщается на случай любого числа тел и любых консервативных сил взаимодействия между ними. Под E_к нужно понимать сумму кинетических энергий всех тел, а под Е_п - полную потенциальную энергию системы.    Для системы, состоящей из тела массой m и пружины, закон сохранения механической энергии имеет вид

   Полная механическая энергия системы равна сумме ее кинетической и потенциальной энергий. В изолированной системе, в которой действуют только консервативные силы, механическая энергия сохраняется.