1) Limx-08x/sinx

2) Limx-0sin8x/X

25. Расположите пределы по возрастанию их значений:

4)

2)

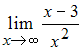
3)

1)

X²-8x+12

26. Вычислить: lim_x-2-----------

x-2

2) –4

3X³-8x²-5

27. Вычислить: lim_x-беск-----------

2х²

2) бесконечность

28 . Точка х = 1 для функции является …

1) Точкой непрерывности

29. Точка х = -4 для функции является:

1) Точкой разрыва II рода

30. Точка х = - 6 для функции является:

2) Точкой разрыва II рода

31. Вычислить f^/(2), если f(x)=1/x⁴:

3)-1/8

32. Вычислить f^/(-1), если f(х)=9х²+х-1

2) –17

33. Вычислить f^/(-1), если f(х)=1/3х³+3/2 х²+8:

3) 4

34. Производная функции у = 3arcsin x в точке х₀ = 0 равна:

2) 3

35. Производная функции имеет вид :

1)

36. Установите соответствие между функциями и их производными

(укажите соответствие для каждого нумерованного элемента задания)

1.	F(x)=√2x+1		А	F/(x)=1/√x+1
2.	F(x)=2√x+1		Б	F/(x)=1/√2x+1
3.	F(x)=√x+2		В	F/(x)=1/2√x+2

Ответ: 1-Б, 2-А, 3-В

37. Производная функции у = sin (5 – 2х) имеет вид:

1) у’ = - 2cos (5 – 2x)

38. Производная функции у=2е^3х-5 равна:

3) 6е^3х-5

39. Производная функции y=2ln(4х-3)=8 равна:

3) 8/4х-3

40. Установите соответствие между функциями и их производными.

1.	F(x)=x+2+ех		А	F/(x)=1+ех
2.	F(x)=x2+ех		Б	F/(x)=2+ех
3.	F(x)=x+2ех		В	F/(x)=1+2ех

Ответ: 1-А, 2-Б, 3-В

41. Вторая производная у’’(х) функции у(х) = 3х – 6х² + 1 имеет вид …

1) у^//=-12

42. Укажите промежуток, на котором производная функции y=f(x),

представленной на рисунке, положительна:

4) (0;2)

43. Указать промежуток, в котором производная функции y=f(x), отрицательна:

4) (-2;1)

44. Найдите значение производной функции y=f(x), в точке x₀.

4) 1

45. Материальная точка движется прямолинейно и неравномерно по

закону . Её мгновенная скорость через 2 сек после начала движения равна:

1. 26 м/c

46. Материальная точка движется прямолинейно и неравномерно со скоростью . Её ускорение через 2 сек после начала движения равно:

2) 15 м/c²

47. Угловой коэффициент касательной к графику функции у = 3+8х-3х²

в точке х₀ = 2 равен:

4) -4

48. Найти промежутки возрастания функции f(x) = x³ - 3x² +1

2) (-беск;0)U(2; +беск)

49. Найти промежутки убывания функции f(x) = x⁴ - 4x + 3

1) (-беск; 1)

50. Найти максимум функции f(x) = x³ - 4x

1) 16/3

51. Найти минимум функции f(x) = 2x³ - 9x² + 12x - 8

2) -4

52. Найти интервалы выпуклости вверх графика функции y = 4x³ - 6x²

2) (-беск; 0,5)

53. Найти промежутки выпуклости вниз графика функции y = x³ -3x²

4) (1; +беск)

54. Указать абсциссу точки перегиба графика функции

y = 2x³ - 6x² - 12x - 1

1) 1

55. Абсциссой точки перегиба графика функции у = 8х² - х³ – 2

является:

4) 2

56. Расположите функции, определенные на всей числовой прямой,

знаки производных которых указаны на рисунках, по возрастанию

количества точек максимума

А			4
Б			2
В			1
Г			3

Ответ: А-4, Б-2, В-1, Г-3.

57. Указать абсциссу точки графика функции f(x)=4 (x-6)² -3, в которой

касательная параллельна оси ОХ.

3) 6

58. Указать абсциссу точки графика функции , в которой

касательная наклонена к оси ОХ под углом :

1) -1

59 . Множество всех первообразных функции имеет

вид:

3) - 3ctgx + C

60. Множество всех первообразных функции

 

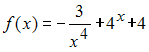
имеет вид:

4) 1/о^//3+4^//о/ln4+4х+С

61. Найти

3) х⁴-х²+3х+С

62. Найти интерграл(3х⁵….

2) х⁶/2+2х²-5х+С

63. В результате подстановки t = 4x + 3 интервал приводится к

виду:

2)

64. Установите соответствие между интегралами и методами их

вычисления:

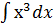
1.			А	непосредственное интегрирование
2.			Б	метод замены переменной
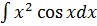
3.			В	метод интегрирования по частям

Ответ:1-А; 2-Б; 3-В

65. Найти интерграл е^(3х-1)dx

3) 1/3e^(3x-1)+C

66. Найти интерграл sin(5x+6)dx

1) -1/5cos(5x+6)+C

67. Вычислить интерграл от 0 до 2 (х³+3х²)dx

3)12

68. Используя свойства определенного интеграла, интеграл

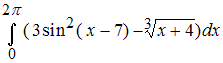
можно привести к виду:

1) 3интеграла от 0 до 2П sin²(x-7)dx + int 2П;0 корень³х+4 dx

69. Несобственным интегралом является интеграл: