12. Определение.

Схемы цифровых логических устройств обычно состоят из комбинационных элементов, таких, как И-НЕ и ИЛИ-НЕ, и элементов памяти. В качестве элементов памяти могут выступать, с одной стороны, однобитовые элементы памяти, такие, как дискретные триггеры, а с другой - цепочки триггеров. Цепочка триггеров используются, например, в сдвиговых регистрах.

Появление нового компонента цифровых систем – памяти приводит к необходимости введения дополнительной переменной, а именно, времени. Эта переменная должна учитываться при решении многих задач, связанных с проектированием цифровых систем. С появлением памяти стало возможно логические операции выполнять последовательно, так как информация может храниться в памяти и в нужные моменты выбираться оттуда для управления операциями комбинационной логики Схемы, работающие таким образом, называются последовательными.

5.2. Т-триггер

Условное обозначение Т-триггера дано на рис. 5.1, а. Это устройство имеет один вход Т и взаимно дополняющие друг друга выходы Q и 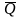. Продемонстрировать работу триггера можно с помощью диаграммы состояний (рис. 5.1, б). На диаграмме состояний триггеры представлены двумя квадратами, т. е. имеются два возможных состояния триггера, Q = 0 и Q = 1, которые связаны с внешним миром. Переходы из одного состояния в другое показаны сплошными линиями, а стрелки указывают направления переходов. Сигнал, вызывающий переход, размещается под стрелкой. Анализ рис. 5.1, б показывает, что если триггер находится в состоянии Q = 0 и на его вход поступает сигнал Т, то он переходит в альтернативное состояние Q = 1. С другой стороны, если в состоянии Q = 1 на вход триггера проходит сигнал Т, он переходит в состояние Q = 0. Иначе говоря, триггер меняет свое состояние каждый раз, когда приходит сигнал на вход Т.

Понятие диаграммы состояний является фундаментальным для проектировщиков цифровых систем. Если удается описать задачу с помощью диаграммы состояний или последовательности диаграмм состояний, то обычно нетрудно перейти от такого рода диаграмм непосредственно к аппаратной реализации.

Существует два типа диаграмм состояний. На рис. 5.1, б дан пример диаграммы внешних состояний. В этом случае поведение триггера описывается с помощью двух состояний, которые связаны с внешним миром. В то же время нет ссылок на внутренние состояния, в которых схема может находиться при переходе из состояния Q = 0 в состояние Q = 1 и наоборот. В действительности можно описать поведение Т-триггера с помощью внутренних состояний. Такое описание получило название диаграммы внутренних состояний. Применение диаграмм внутренних состояний может оказаться полезным проектировщику цифровых логических устройств.

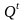Вторым важным методом, используемым для описания функционирования Т-триггера, является метод таблиц состояний. На рис. 5.1, в изображена таблица состоянии Т-триггера. Она разделена на две части: левую и правую. Левая часть отражает текущее состояние входа и текущее состояние триггера , правая - следующее состояние триггера . Следующее состояние триггера зависит от текущих состояний триггера и входа. Состояние триггера может измениться только через время t после подачи входного сигнала.

Таблицу состояний строят точно таким же путем, как таблицу истинности. Первые два столбца таблицы содержат все возможные комбинации значений текущих состоянии Т и Q , а первую строка таблицы интерпретируют следующим образом:

если значение Т не меняется в момент времени t и остается равным 0, то не будет меняться и состояние триггера, т. е. .

Аналогично интерпретируется и третья строка: если значение Т меняется с 0 на 1 в момент времени t, то состояние триггера, которое соответствовало значению Q = 0, изменится на Q = 1 в момент времени t+t.

Из таблицы состояний может быть получено уравнение, описывающее поведение триггера. Это уравнение носит название характеристического уравнения триггера. Оно показывает, как меняется состояние триггера в зависимости от текущих значений состояния и входа, и имеет вид

.

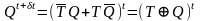Выражение, стоящее справа от знака равенства, является дизъюнктивной нормальной формой. На рис. 5.1, г показано, как оно может быть реализовано с помощью элементов И-НЕ.

Имеются два важных момента, которые следует отметить. Так, уравнения, полученные из таблицы состояний, являются булевыми уравнениями. Они отличаются от обычных комбинационных уравнений, рассмотренных выше: в них явно учитывается время, и значение Q в правой части уравнения может отличаться от значения Q в его левой части, так как эти два значения относятся к разным моментам времени. Вторым важным моментом является то, что схема, показанная на рис. 5.1, г, только условно может считаться комбинационной. Анализ этой схемы показывает, что ее выход связан с входом и, следовательно, существует обратная связь.

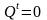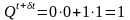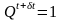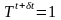К сожалению, схема, изображенная на рис. 5.1, г, будет работать неудовлетворительно по следующей причине: если и , то . Следовательно, имеет месте переход из одного состояния в другое в момент времени t+t . Если допустить, что сигнал Т еще не успел стать равным 0 в момент временя , то имеем и . Тогда

,

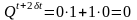т. е. осуществляется переход 1  0 в момент времени t+2t .

Значение выходного сигнала Q будет становиться равным то 0, то 1 до тех пор, пока Т не станет равным 0. Этот процесс показан на рис. 5.1, д. Более того, окончательное значение будет зависеть от длительности промежутка времени, в течение которого подавался сигнал Т, и от времени задержки t схемы. Поэтому говорят, что выходное состояние Q неопределенно.

Когда осуществляется переход 1  0 для Т, то никакого изменения выходного сигнала триггера Q не происходит. Что это действительно так, позволяет понять характеристическое уравнение.

Если и Т меняется с 1 на 0 в момент времени t , то

.

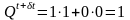Рис. 5.2. SR-триггер:

а – условное обозначение; б – таблица состояний; в – диаграмма внешних состояний; г – карта Карно; д – реализация характеристического уравнения на элементах И-НЕ; е – условное представление SR-триггера; ж – реализация характеристического уравнения на элементах ИЛИ-НЕ; з – управляющая таблица SR-триггера; и – синхронизация (C_u) SR-триггера; к – временная диаграмма; л – управляющие входы очистки и предустановки; м – таблица описывающая работу триггера, снабженного входами очистки и предустановки; н – диаграмма внешних состояний, учитывающая входы очистки и предустановки

С другой стороны, если и осуществляется переход 1  0 для Т в момент времени t , то

Причиной нестабильности схемы Т-триггера, изображенной на рис. 5.2, г, является возникновение гонок. Если новое значение Q , сформировавшееся в момент времени t , подать на входы элементов g₂ и g₃ до того, как будет прекращена подача сигнала Т , произойдет новое изменение состояния Q . Эта ситуация хорошо иллюстрируется временной диаграммой, изображенной на рис. 5.1, д. Разбор диаграммы показывает, что если t  t, то налицо нестабильность. Ниже в этой главе будет описан более удовлетворительный способ построения схемы Т-триггера.

13. . SR-триггер

Условное обозначение SR-триггера дано на рис. 5.2, а. Входы установки и сброса обозначены S и R , соответственно, а взаимно дополняющие друг друга выходы – Q и .

Таблица состояния триггера показана на рис. 5.2, б. В ее первых трех столбцах расположены все возможные комбинации текущих состояний S, R и Q, т.е. значения сигналов, характеризующих эти состояния в момент времени t. Четвертый столбец отражает состояние триггера в момент времени t+t.

Анализ таблицы показывает, что только в ситуациях, описываемых строками 4 и 5, происходит изменение состояния триггера.

Рассмотрим строку 4. После того, как подается сигнал на вход R, триггер запирается, т.е. переходит из состояния 1 в состояние 0. Рассмотрим строку 5. Триггер отпирается, т.е. переходит из состояния 0 в состояние 1, в результате подачи сигнала на вход S.

Для строк 1 и 2 S=0 и R=0 и, следовательно, никаких изменений в состоянии триггера не происходит (отражающие это записи в последнем столбце остаются равными 0 и 1, соответственно). Для строки 3 R = 1, и этот сигнал в нормальных условиях должен запереть триггер, но так как триггер уже заперт и Q^t = 0, то сигнал R = 1 не изменяет его состояния.

Аналогично для строки 6 S = 1, и этот сигнал будет в обычных условиях отпирать триггер, но Q^t = 1, и, следовательно, состояние триггера останется без изменения. Наконец, для этого типа триггеров запрещено, чтобы на входах S и R одновременно присутствовали логические «1». Это условие может быть выражено алгебраически SR =0.

Итак, условие отпирания триггера имеет вид

отпирание = ,

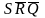а условие запирания задается как

запирание = .

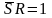С учетом этих двух условий диаграмма внешних состояний примет вид, показанный на рис. 5.2, в. Анализ диаграммы показывает, что переход из состояния Q = 0 в состояние Q = 1 происходит, если , а обратный переход осуществляется, если . Характеристическое уравнение триггера получается в результате выполнения операции логического сложения конъюнкций переменных, для которых , и терма SR. Добавление терма SR не оказывает влияния на значение , но ведет к упрощению выражения. Следовательно,

.

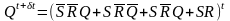На рис. 5.2, д приведено изображение этой функции с помощью карты Карно. Терм SR является «термом, не доставляющим беспокойства», и ему на карте Карно соответствуют ячейки, помеченные символом «d». Упрощая это выражение, получаем характеристическое уравнение в виде

где S и R - отпирающий и запирающий входы, соответственно.

На рис. 5.2, д показано, как это уравнение можно реализовать на элементах И-НЕ. Условно эта схема может быть изображена так, как показано на рис. 5.2, е. Уравнение для выхода Q имеет вид

.

Тогда для выхода элемента 4 получаем

,

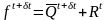а подстановка значения для

.

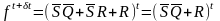Анализ карты Карно (рис. 5.2, г) показывает, что функция, которой соответствуют ячейки, помеченные «0», а к которой

могут быть присоединены ячейки, помеченные «d», имеют вид

.

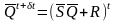Следовательно,

,

и выход элемента 4 является дополнительным выходом триггера.

Вторую форму характеристического уравнения получаем путем исключения терма SR из уравнения для .

Тогда

.

Эти три терма соответствуют трем «1», присутствующим на карте Карно (рис. 5.2, в).

Упрощая выражение, стоящее справа, получаем

.

Это двухуровневая конъюнктивная нормальная форма. На рис. 5.2, ж дана ее реализация на элементах ИЛИ-НЕ.

Работа SR-триггера может быть описана с помощью управляющей таблицы (рис. 5.2, з). Эта таблица немного отличается от таблицы состояний. Два ее первых столбца характеризуют все возможные переходы триггера, в то время как два последних показывают, при каких значениях S и R эти переходы происходят. Например, первая строка показывает, что переход 0  0 будет происходить только, если S = 0, a R = 0 или R = 1. Так как значение R может быть равно как 0, так и 1, то на пересечении первой строки и четвертого столбца записывается символ 0. Для второй строки, описывающей переход 0  1, находим, что S = 1. Так как S и R одновременно не могут равняться 1, то, следовательно, значение входа R равно 0. Значения S и R для оставшихся двух строк могут быть определены аналогично.

С помощью незначительной модификация SR-триггер может быть синхронизирован (рис. 5.2, и). Анализ диаграммы показывает, что если сигнал синхронизации Си = 0, то на выходах элементов g₁ и g₂ всегда логические «1» независимо от текущих значений S и R и от любых изменений, связанных с сигналами на этих входах, следует отметить, что триггер может изменить свое состояние только во время изменений значений сигнала синхронизации. Считая задержку элементов схемы равной нулю, получим, что значение Q, будет изменяться во время формирования положительного фронте импульса синхронизации, когда сигнал Сu изменяется от 0 до 1 (рис. 5.2, к).

Кроме входов S, R и Си SR-триггер может иметь один или два дополнительных управляющих входа. Эти входы дают возможность триггеру менять свое состояние независимо от того, Си = 1 или Си = 0. Управляющие входы обычно называют входами очистки и предустановки. Большинство используемых на практике триггеров снабжаются входами очистки, в то время как вход предустановки не является обязательным. Действие этих управляющих входов описывается с помощью таблицы на рис. 5.2, м. Следует отметить, что в схеме, изображенной на рис. 5.2, л. управляющие сигналы проходят на выходы элементов И-НЕ только тогда, когда их значение равно 0.

Если на обоих управляющих входах логические «l», то триггер работает как обычно. Если r = 0 и р = 1, то выход элемента g₄ на рис. 5.2, л принимает значение 1. Следовательно, Q = 0, и триггер запирается. Если r = 1 и р = 0, выход Q элемента g₃ принимает значение 1, и триггер отпирается. Если на линии р и r подать логический «0», то это приведет к подавлению сигналов на входах S и R. Появление двух управляющих входов, естественно, изменит диаграмму внешних состояний. Новая диаграмма показана на рис. 5.2, и. Читатель, должно быть, заметил, что в том случае, когда изготовителем не предусмотрен вход р, нужна предварительная установка триггера. Иначе можно перепутать выхода Q и и входы S и R. Для предварительной установки можно использовать вход очистки.

5.4. JK-триггер

На рис, 5.3, а приведено условное обозначение JK-триггера. Логика его работы описывается с помощью таблицы состояний, изображенной на рис. 5.3, б.