4.11. Двоичное умножение

Один из самых простых и наиболее быстрых методов умножения основан на использовании комбинационной логической схемы, состоящей из элементов И, сумматоров и полусумматоров. В его основу положено то, что правило булевого и двоичного умножения одинаковы, и поэтому группы элементов И могут использоваться для формирования частичных произведений, которые возникают в процессе двоичного умножения.

Р ис. 4.8. Схема, реализующая операцию умножения двух чисел:

а - двоичное умножение; б - параллельное двоичное устройство умножения

Если, например, требуется найти произведение двух трехразрядных двоичных чисел А₂А₁А₀ и В₂В₁В₀, то обычно используют хорошо известный метод, который проиллюстрирован на рис. 4.8, а. Сначала наименьший значащий разряд множителя по очереди умножают на каждый разряд множимого, формируя три конъюнктивных терма первой строки А₂В₀, А₁В₀ и А₀В₀ . Следующую строку конъюнкций получают так: осуществляют сдвиг влево, и затем каждый разряд множимого умножают на следующий за наименьшим разряд множителя. Остальные строки формируют аналогично. Процесс закончится, когда будут исчерпаны все разряды множителя. После этого содержимое столбцов складывают по очереди справа налево. В результате получают все цифры (от Р₀ до P₅) произведения.

При формировании разрядов от Р₁ до Р₅ необходимо учитывать возможность образование переноса. Во втором столбце справа откладывают А₁В₀ и А₀В₁ , образуя Р₁. Выполняя эту операцию, надо учитывать возможность образования единицы переноса С₁, которая должна быть добавлена в следующий столбец для суммирования. Для третьего столбца должны быть выполнены две операции сложения, так как складываются четыре слагаемых. 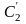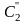Это приводит к возможности образования двух единиц переноса и , которые помещают в следующий столбец и т.д.

Логическая схема устройства умножения показана на рис. 4.8, б. Следует отметить, что число элементов, необходимых для реализации устройства умножения параллельного действия, быстро растет с ростом числа разрядов множителя и множимого. До появления БИС большое количество элементов комбинационной логики, требуемых для реализации схемы, было препятствием для использования этого метода. Но сейчас, когда БИС получили широкое распространение, появились реализующие этот метод устройства, размещенные на одном кристалле.

11. Преобразователь из двоичного кода в код Грея

Другой широко используемый код – это одношаговый код, обычно называемый кодом Грея. Отметим характерную особенность этого кода: при переходе к следующей кодовой комбинации меняется только одна цифра.

С уществует несколько кодов Грея. В частности, один можно получить, беря по модулю два сумму соседних цифр четырехбитного двоичного кода. Например, десятичная цифра 3 в четырехразрядном двоичном коде имеет вид 0011. Ниже показано, как эта комбинация преобразуется в соответствующую комбинацию в коде Грея. При проведении этого преобразования следует считать, сто второй бит, который участвует в формировании В₃ , равен 0.

Анализ приведенного выше преобразования показывает, что цифры G₃ , G₂ , G₁ и G₀ кода Грея связаны с двоичными цифрами В₃ , В₂ , В₁ и В₀ следующими соотношениями:

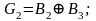
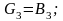
Логическая схема, реализующая эти соотношения, приведена на рис. 4.10, а, а на рис. 4.10, б изображены соответствующие друг другу комбинации в двоично-десятичном коде и коде Грея. Для реализации схемы требуется только элементы ИСКЛЮЧАЮЩЕЕ ИЛИ, которые имеются во многих сериях ТТЛ-логики.

Данная форма кода Грея называется отраженной двоичной. Если провести горизонтальную линию ниже кодовой комбинации 0100 (см. рис. 4.10, б), то будет видно, что последние три цифры кодовых комбинаций, расположенных ниже этой линии, совпадают с соответствующими цифрами кодовых комбинаций, расположенных симметрично по отношению к этой линии.

Чтобы получить логические уравнения для обратного преобразования, строят карту Карно для всех двоичных цифр В₃ , В₂ , В₁ и В₀ . Переменные связанные со строками и столбцами карт, являются отдельные разряды кода Грея G₃ , G₂ , G₁ и G₀ . На рис. 4.10, в приведена карта Карно обратного преобразования.

Карта Карно для В₀ похожа на шахматную доскуи соответствует функции ИСКЛЮЧАЮЩЕЕ ИЛИ. Следовательно,

.

Функции В₁ , В₂ и В₃ имеют следующий вид:

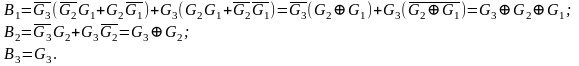
Логические схемы, реализующие эти функции, приведены на рис. 4.10, г. Ясно, что и в данном случае для реализации преобразователя кодой потребуются только элементы ИСКЛЮЧАЮЩЕЕ ИЛИ.