9. Полусумматор

П олусумматор является одной из простейших комбинационных логических схем. Полусумматор используется для сложения двух наименьших значащих цифр при двоичном суммировании, как показано на рис. 4.2. а. При сложении двух двоичных цифр А и В существуют четыре различные комбинации, которые показаны на рис. 4.2, б. В каждом из четырех случаев ищут сумму двух цифр, но следует заметить, что в последнем случае, когда А = 1 и В = 1, появляется еще и единица переноса, которая должна быть учтена на следующей стадии выполнения операции сложения, где ее прибавляют к сумме.

Рис. 4.2. Полусумматор:

а - двоичное сложение; полусумматор используется для сложения двух наименьших значащих цифр (обведены штриховой линией}; б - четыре различные случая, возникающих при сложении двух двоичных цифр А и В (с переносом, который учитывается на следующей стадии сложения); в - таблица истинности полусумматора; г - реализация полусумматора на элементах И-НЕ

Все случаи суммирования двух двоичных цифр, отраженные на рис. 4.2, б, сведены в таблицу (рис. 4.2, в). В ее столбцах А и В расположены значения переменных, которые необходимо сложить. В третьем и четвертом столбцах таблицы хранятся сумма S и перенос С, соответственно. Анализ таблицы позволяет определить булевы функции для S и С

т. е. значения S = 1 дают две комбинации переменных. Таким образом, получаем, что S соответствует функция ИСКЛЮЧАЮЩЕЕ ИЛИ с двумя входами

.

Для С устанавливаем

С = АВ.

На рис. 4.2, а показана реализация функций суммы и переноса на элементах И-НЕ.

4.3. Полный сумматор

Для сложения наименьших значащих цифр требуется полусумматор, а для сложения всех остальных цифр - полный сумматор. Как показано на рис. 4.3, а, схема полного сумматора содержит три входа: два соответствуют двоичным цифрам А и В, а третий – переносу из предыдущего разряда С_вх . Кроме того, схема имеет два выхода: сумму S и перенос в следующий разряд С_вых

На рис. 4,3, б изображена таблица истинности полного сумматора. Анализируя эту таблицу, получаем булевы выражения для суммы S и переноса в следующий разряд С_вых:

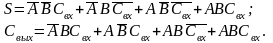
Выражение для суммы может быть приведено к виду

.

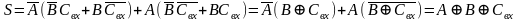Рис. 4.3. Полный сумматор:

а - структурная схема; б - таблица истинности; в - карта Карно для С_вых; г - реализация

На рис. 4.3, в представлена карта Карно для С_вых . Проведя упрощение, получаем, что

.

Схема полного сумматора дана на рис. 4.3, г.

4.4 Четырехразрядный сумматор параллельного действия

Теперь уже не составит труда построить, например, четырехразрядный сумматор параллельного действий из четырех одноразрядных полных сумматоров. На рис. 4.4 показана структурная схема многоразрядного сумматора. Заметим, что для полного сумматора, производящего сложение младших разрядов чисел, линия переноса C_-1 заземлена, т. е. значением C_-1 всегда является логический «0».

Иногда схемы такого типа называют сумматорами со сквозным переносом, поскольку перенос, полученный на какой-нибудь стадии суммирования, может распространиться и на последующие стадии. В худшем случае перенос, сформированный сумматором FA₀ , может пройти по всем четырем линиям переноса и только после этого появится на выходе последнего сумматора FA₃. Например, пусть требуется сложить следующие два числа:

А 1 1 1 1 15

+

В 1 0 0 1 9

----------------

1 1 0 0 0 24

В этом случае перенос возникает при суммировании самых младших разрядов и распространяется на все старшие разряды. В конце концов он появляется на выходе С₃ сумматора старших разрядов, где становится первой значащей цифрой результата. Следовательно, сигнал переноса проходит последовательно четыре двухуровневые логические схемы, и сумма не может быть полностью сформирована до тех пор, пока не пройдет время, равное сумме задержек восьми элементов. Таким образом для сумматоров этого типа максимальная задержка прямо пропорциональна числу разрядов (или стадий суммирования) n.