2.9. Термы, «не доставляющие беспокойства»

Следует отметить, что при решении некоторых логических задач определенные комбинации переменных могут никогда не использоваться. Например, для представления десятичных цифр часто используют код NBCD (рис. 2.13, а). Это четырех битовый код с 16 возможными комбинациями, но только десять из них применяют на практике. Оставшиеся шесть комбинаций, а именно 1010, 1011, 1100, 1101, 1110 и 1111, появиться не могут и, следовательно, могут быть использованы для целей упрощения представления функций. Такие термы называют «термами, не доставляющими беспокойства».

Для распознавания цифр, представленных в NBCD-коде, используют декодирующее логическое устройство (рис. 2.13, б). Очевидно, что для его реализации потребуется десять независимых схем, по одной для каждой цифры.

Для определения функций, реализуемых каждой схемой, используют карту Карно, изображенную на рис. 2.13, в. На этой карте термы, «не доставляющие беспокойства», помечают символами «d», а оставшиеся десять ячеек - десятичными цифрами, соответствующими кодам ячеек. Например, ячейка, определяемая термом 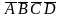-0000, помечается десятичной цифрой «0». Найти комбинации этой ячейки с ячейками, помеченными «d», не удается. Следовательно, .

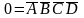Аналогично, ячейка, помеченная десятичной цифрой 1, не может быть объединена с хотя бы одной ячейкой, помеченной, «d». Поэтому .

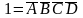Рис. 2.13. Дешифратор для кода NBCD:

а - код NBCD; б - структурная схема дешифратора; в - карта Карно, служащая для определения логических функций реализуемых дешифратором; г - реализация дешифратора

О днако ячейка, помеченная десятичной цифрой «2», может быть объединена с ячейкой, помеченной «d», как это показано на рис. 2.13, в. Следовательно, .

Функции, соответствующие оставшимся десятичным цифрам, могут быть найдены тем же самым путем. Приведем их:

Реализация всех найденных функций показана на рис. 2.13, г.

Это декодирующее логическое устройство является примером комбинационной логической схемы. Любая комбинационная логическая схема характеризуется тем, что ее выход полностью определяется сигналами на входах.

7. Реализация дизъюнктивных нормальных форм с помощью элементов и-не

Функция f = АВ + CD считается выраженной в дизъюнктивной нормальной форме. На рис. 3.4, а показана реализация этой функции с помощью элементов И/ИЛИ. На этом же рисунке выделены два уровня расположения элементов в схеме: на первом уровне размещен элемент ИЛИ, на втором - два элемента И. Данную схему можно преобразовать в схему, построенную на элементах И-НЕ, используя правила, изложенные в п. 3.3. Процедура преобразования показана на рис. 3.4, б. Первый блок, обведенный штриховыми линиями, представляет собой два элемента И, а второй - элемент ИЛИ. Можно заметить, что в обеих ветвях схемы присутствуют по два одновходовых элемента И-НЕ, которые будут производить двойную инверсию сигналов и 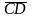. Поэтому четыре элемента И-НЕ являются лишними (на рис. 3.4, б они перечеркнуты). После удаления этих элементов схема принимает вид, приведенный на рис. 3.4, в.

Из рассмотренного примера ясно, что схемы, построенные на элементах И/ИЛИ, очень просто (практически «один к одному») преобразовать в схемы, реализуемые на элементах И-НЕ.

Даже функция более сложного вида, такая, как

.

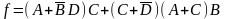может быть представлена в дизъюнктивной нормальной форме f=PQ+SRT,

где 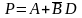; S=С+D; Q=С; R=A+С; T=В.

Рас. 3.5. Реализация на элементах И-НЕ:

а - план реализации f; б - реализация на элементах И-НЕ; в - реализация f

Реализация f=PQ+SRT показана на рис. 3.5, а. Для того чтобы реализовать терм на элементах И-НЕ, требуется одна схема И-НЕ с входами, представляющими отрицания переменных, которые необходимо получить на выходе (рис. 3.5, б). На рис. 3.5, в представлена полная схема, используемая для реализации искомой функции.

Описанные методы представления булевых функций с помощью элементов И-НЕ не обязательно приводят к минимальной реализации. Однако иногда, используя процесс факторизации, достаточно просто получить реализацию на элементах И-НЕ, состоящую из меньшего числа элементов.

В качестве примера возьмем функцию .

Непосредственная реализация этой функции приводит к схеме, изображенной на рис. 3.6, а, которая требует следующих элементов И-НЕ: одного с тремя входами, трех с двумя входами и двух с одним входом (на практике элементы И-НЕ, значения всех входов которых равны логической «1», используются в качестве инверторов). Однако эта же функция может быть представлена в виде

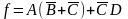
и реализована на элементах И-НЕ так, как показано на рис. 3.6, б.

Рис. 3.6. Три способа (а, б, в) реализации функции на элементах И-НЕ

Кроме того, функцию f можно представить и так:

.

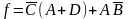Тогда для реализации потребуется восемь элементов И-НЕ (рис. 3.6, в).

Очевидно, что для реализации схемы, показанной на рис. 3.6, б, потребуется меньше элементов И-НЕ, чем для схем, представленных на рис. 3.6, а и 3.6, в. Зиссос предложил формальный метод определения минимальной по числу элементов И-НЕ реализации при условии соблюдения ограничении, накладываемых на число входов. Этот метод основан на использовании принципа слияния, дающего возможность преобразовать выражения в скобках, например 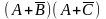, к виду . В одних случаях слияние позволяет уменьшить число элементов в схеме, в других же, наоборот, приводит к их увеличению. Метод Зиссоса позволяет определить влияние процесса слияния на количество элементов И-НЕ, необходимых для реализации схемы логической функции.