6. Представление булевых функций с помощью карт Карно

Для функции двух переменных карта Карно содержит четыре ячейки, по одной для каждого Р-терма. Изображение функций 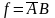с помощью карты Карно показано на рис. 2.7, а. В первую верхнюю ячейку карты записывают «1».

Рассмотрим теперь функцию двух переменных А и В, f = А. Применяя теорему дополнительности, получаем.

.

Эта функция изображена на рис. 2.7, б. Заполнены только нижние ячейки карты. Следовательно, при представлении с помощью карты Карно функции двух переменных, зависящей только от одной из них, заполняют две соседние ячейки.

Так как для трех переменных существуют восемь Р-термов, для функции трех переменных f (А, В, С) потребуется восьми ячеечная карта Карно (рис. 2.8, а). На этой карте изображена функция . Поскольку помеченные «1» ячейки карты не являются соседними, два составляющих функцию Р-терма не могут быть объединены и, следовательно, функция f не может б ыть упрощена.

На рис. 2.8, б изображена карта Карно, представляющая состоящий из двух переменных терм ВС; на этой карте заполнены только две ячейки. Анализ карты показывает, что терм ВС является логической суммой Р-термов АВС и , т, е.

Состоящий из одной переменной терм занимает четыре соседние ячейки на карте, предназначенной для представления функций, зависящих от трех переменных. Например, карта Карно для терма изображена на рис. 2.8, в. Кажется, что четыре ячейки, помеченные «1», не являются соседними. Однако, если свернуть карту в вертикальный цилиндр, то будет видно, что первый и последний столбцы расположены рядом.

Рис. 2.6. Карты Карно для:

а - трех переменных; б - четырех переменных; в - пяти переменных: г - шести переменных

Рис. 2.7. Представление с помощью карты Kapно функции:

а - ; б -

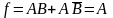
На карте Карно, рассчитанной на представление функций, зависящих от четырех переменных, Р-терм также занимает одну ячейку (рис. 2.9, а). В связи с этим термы, состоящие из трех, двух и одной переменной, при размещении на карте Карно займут две, четыре и восемь ячеек, соответственно, как показано на рис. 2.9, б, в, г. Анализ рис. 2.9, г показывает, что, во-первых, верхняя и нижняя строки карты Карно могут считаться соседними и, во-вторых, как и в случае с картой Карно для трех переменных, первый и последний столбцы также могут считаться соседними.

2.7. Упрощение булевых функций

Процесс упрощения булевых функций с помощью карт Карно основан на поиске соседних заполненных ячеек. Поясним это на примере функций

.

Здесь функция f представлена в виде логической суммы Р-термов, каждый из которых заменен стоящим под знаком суммы индексом. Изображение функции с помощью карты Карно показано на рис. 2.10. На карте можно выделить четыре группы соседних ячеек: три группы содержат по четыре ячейки и одна группа - две ячейки. 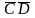Четыре ячейки в верхней строке карты соответствуют терму , четыре ячейки первого столбца – терму , четыре ячейки справа вверху - терму и, наконец, две соседние ячейки - терму . Следовательно, после упрощения функция примет вид

.

Т ермы, входящие в состав упрощенной функции, обычно называют главными импликантами.

Теперь стало ясным, почему переменные С и D, а также А и В связаны со строками и столбцами именно таким способам, как описано выше. Используемый способ гарантирует, что ячейки, связанные с переменными 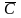, С, и D, всегда принадлежат двум соседним столбцам, в то время как ячейки, связанные с переменными , А, и В, всегда принадлежат соседним строкам. Если бы переменные были связаны с ячейками карты в строгом соответствии с числовым порядком, определяемым двоичными кодами 00, 01, 10 и 11, тогда ячейка, связанные, например, с D, не принадлежали бы соседним столбцам, и процесс упрощения не мог бы быть сведен к обнаружению соседних заполненных ячеек карты Карно.

Р ис. 2.10. Карта. Kapно для функции

Р ис. 2.11. Карта Карно для функции

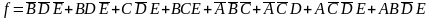
Упрощение функций, зависящих от пяти переменных, - несколько более сложный процесс. Рассмотрим функций

.

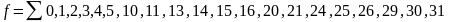Представляющая ее карта Карно изображена на рис. 2.11. Ниже приведена процедура упрощения этой функции.

1. Сначала описанным ранее способом находим упрощенные формы представления для двух функци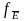й и 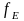, соответствующих левой и правой частям карты Карно на рис. 2.11:

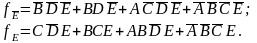
2. Второй шаг заключается в поиске таких главных импликант двух функций и , которые можно объединить. В результате получим упрощенную форму логической суммы двух функций

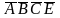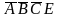Например, - главная импликанта и - главная импликанта . Эти две импликанты можно объединить, получив в результате терм, состоящий из трех переменных . Также возможно дополнить функцию несущественной главной импликантой . Объединив ее с главной импликантой 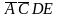функции , получим терм . Этот процесс можно изобразить так:

Таким образом, упрощенная форма функции имеет вид