
- •2. Функция и-не. Реализация функций и, или, не с помощью элементов и-не.
- •3. Теорема идемпотентности.
- •4. Определение дополнения функции
- •6. Представление булевых функций с помощью карт Карно
- •2.7. Упрощение булевых функций
- •2.9. Термы, «не доставляющие беспокойства»
- •7. Реализация дизъюнктивных нормальных форм с помощью элементов и-не
- •9. Полусумматор
- •4.3. Полный сумматор
- •4.4 Четырехразрядный сумматор параллельного действия
- •10. Дополнительный код
- •4.8. Обратный код
- •4.9. Двоичное представление чисел
- •4.11. Двоичное умножение
- •11. Преобразователь из двоичного кода в код Грея
- •12. Определение.
1. Функция «и». Два переключателя x и у соединены последовательно и связывают точки Р и Q (рис. 1.2, а). Пусть состояния переключателей выражаются с помощью двух булевых переменных A и В. Если переключатель x разомкнут, то A = 0, если замкнут, то A = 1. Аналогично, B = 0 или В = 1 в зависимости от того, разомкнут или замкнут переключатель у. Как и в случае одного переключателя, состояние соединения PQ выражается с помощью булевой переменной f, значение которой зависит от наличия связи между точками Р и Q.
С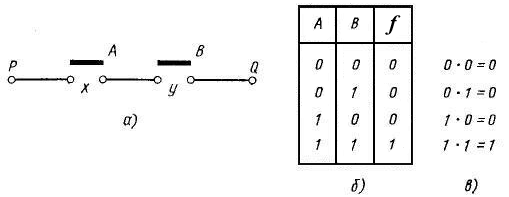 уществует
четыре возможные комбинации
значений
переменных
A
и B.
Они сведены в таблицу истинности,
приведенную на рис. 1.2, б.
Например, если переключатели х
и у
разомкнуты,
то A
= 0, B
= 0, и связи между точками Р
и Q
нет. Следовательно, f
= 0. С другой стороны, если х
и у
замкнуты, то A
= 1,
B
= 1 и, следовательно, f
= 1.
уществует
четыре возможные комбинации
значений
переменных
A
и B.
Они сведены в таблицу истинности,
приведенную на рис. 1.2, б.
Например, если переключатели х
и у
разомкнуты,
то A
= 0, B
= 0, и связи между точками Р
и Q
нет. Следовательно, f
= 0. С другой стороны, если х
и у
замкнуты, то A
= 1,
B
= 1 и, следовательно, f
= 1.
Рис. 1.2. Функция И:
а - переключательная контактная схема, реализующая функцию И; б - таблица истинности функции И; в - правила двоичного и булевого умножения (прав.: 11 = 1)
Функция «или». На рис. 1.4, а два переключателя х и у соединены параллельно и связывают точки Р и Q. Состояния переключателей и соединения PQ выражаются с помощью булевых переменных А, В и f соответственно. На рис. 1.4, б показана таблица истинности этой схемы. Если оба переключателя х и у разомкнуты, то А = 0, В = 0 и ясно, что связи между точками Р и Q нет; следовательно, f = 0. С другой стороны, если переключатель х замкнут, а у разомкнут, то А = 1, В = 0, и связь между точками Р и Q осуществляется с помощью переключателя х; следовательно, f = 1.
Т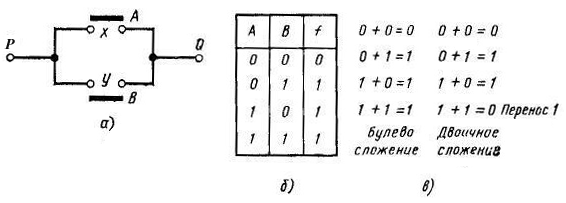 аблица,
изображенная на рис. 1.4, б
является таблицей истинности функции
ИЛИ. Функцию ИЛИ иногда называют функцией
булевого сложения.
Анализ таблицы истинности показывает,
что между точками Р
и Q
существует связь, если переключатель
х
замкнут или переключатель у
замкнут или оба переключателя замкнуты.
аблица,
изображенная на рис. 1.4, б
является таблицей истинности функции
ИЛИ. Функцию ИЛИ иногда называют функцией
булевого сложения.
Анализ таблицы истинности показывает,
что между точками Р
и Q
существует связь, если переключатель
х
замкнут или переключатель у
замкнут или оба переключателя замкнуты.
Рис. 1.4. Функция ИЛИ:
а - переключательная контактная схема, реализующая функцию ИЛИ; б - таблица истинности функции ИЛИ;
в - правила двоичного булевого сложения
Строго говоря, эту функцию следует трактовать как ВКЛЮЧАЮЩЕЕ ИЛИ. Это название можно объяснить так: f = 1 в случае, когда А = 1 и В = 1; другими словами, условие А=1,B=1 включается. Ниже, когда будет определена функция ИСКЛЮЧАЮЩЕЕ ИЛИ, читатель увидит, что условие А = 1, В = 1 исключается, т. е. когда А = 1 и В = 1, значение функции ИСКЛЮЧАЮЩЕЕ ИЛИ будет равно 0.
Функция «не».
В булевой
алгебре есть операции сложения и
умножения, но нет операций деления и
вычитания. Однако в булевой алгебре
существует еще одна фундаментальная
операция - это операция инверсии или
дополнения. Рассмотрим переключательную
схему, изображенную на рис. 1.6, а.
Она состоит из двух связанных
переключателей: если один из них замкнут,
то другой обязательно разомкнут. На
рис. 1.6,а
разомкнутый переключатель представляется
булевой переменной A,
замкнутый - булевой переменной
 .
Для верхнего переключателя А
= 0, когда этот переключатель разомкнут,
а для нижнего переключателя, который
замкнут, когда верхний разомкнут,
= 1. Говорят,
что
есть инверсия A
или НЕ
A.
Следовательно, черта над булевой
переменной A
означает инверсию (или отрицание)
переменной.
.
Для верхнего переключателя А
= 0, когда этот переключатель разомкнут,
а для нижнего переключателя, который
замкнут, когда верхний разомкнут,
= 1. Говорят,
что
есть инверсия A
или НЕ
A.
Следовательно, черта над булевой
переменной A
означает инверсию (или отрицание)
переменной.

Рис.
1.6. Функция
 :
:
а - переключательная схема функции : б - таблица истинности функции
Таблица истинности функции приведена на рис. 1.6, б. Когда A=0 и = 1,то f = 1; аналогично, когда A = 1 и = 0, то f = 1. Это означает, что связь между точками существует всегда и не имеет значения, какой переключатель - верхний или нижний замкнут. Следовательно, уравнение для этой схемы выглядит
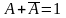 ;
;
это уравнение - алгебраическая запись теоремы дополнительности.
Уравнение, двойственное по отношению к любому булевому уравнению, получается заменой каждого знака «+» на «» и заменой всех 1 на 0 и наоборот. По отношению к вышеприведенному уравнению эта процедура приводит к
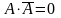
Переключательная контактная схема, соответствующая этому уравнению, показана на рис. 1.7, а, а таблица истинности этой схемы - на рис. 1.7, б.

Рис. 1.7. Функция

а - переключательная схема функции ; б - таблица истинности функции
2. Функция и-не. Реализация функций и, или, не с помощью элементов и-не.
Теперь появилась возможность представлять булевы функции, используя переключательные и электронные схемы. При реализации булевых функций переключательными контактными схемами знаку «+» соответствует пара параллельных ветвей, знаку «•» - последовательное соединение переключателей, а знаку «-» - замкнутый переключатель. Например, функция

может быть реализована на основе переключательных контактных схем (рис. 1.10, а) и на основе электронных схем (рис. 1.10, б). Более сложная булева функция, например,

м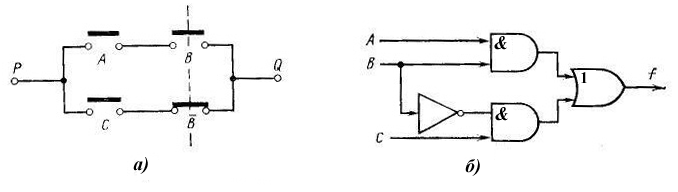 ожет
быть реализована так, как показано на
рис. 1.11,
а
и 1.11, б.
ожет
быть реализована так, как показано на
рис. 1.11,
а
и 1.11, б.
Рис. 1.10. Функция :
а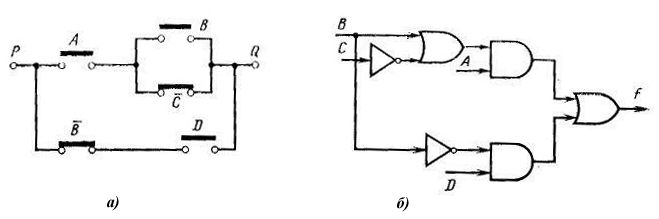 -
реализация функции
с помощью переключателей; б
-
реализация
функции
с
помощью
логических
элементов
-
реализация функции
с помощью переключателей; б
-
реализация
функции
с
помощью
логических
элементов
Рис.
1.11 Реализация функции
 :
:
а - помощью переключательных схем; б - с помощью логических элементов
3. Теорема идемпотентности.
В теореме утверждается, что
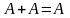
Ясно, что если A = 1, то уравнение приводят к виду
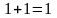
Если же А= 0, то
0 + 0 = 0.
Оба эти результата согласуются с правилами булевого сложения, приведенными на рис. 1.4, в.
Существует
двойственная форма теоремы идемпотентности.
Она может быть получена посредством
применения правил, сформулированных
выше. Ее вид
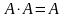 .
.
Если
А =
1, то выражение будет иметь вид .
.
Если
же А = 0, то
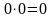 .
.
Д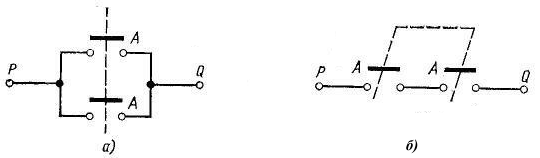 ва
последних результата согласуются с
правилами булевого умножения, приведенными
на рис. 1.2,
в. Для
иллюстрации теоремы на рис. 1.12 приведены
две переключательные контактные схемы.
ва
последних результата согласуются с
правилами булевого умножения, приведенными
на рис. 1.2,
в. Для
иллюстрации теоремы на рис. 1.12 приведены
две переключательные контактные схемы.
Рис. 1.12. Иллюстрация теоремы идемпотентности с помощью переключательных схем:
а
-
реализация
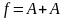 :
б
- реализация
:
б
- реализация

Теоремы объединения и пересечения
В этих теоремах утверждается, что
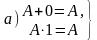 и
и

Представим читателю возможность самому доказать справедливость этих теорем.
Теорема избыточности или поглощения
В этой теореме утверждается, что
А + АВ = А.
Ниже приведено одно из доказательств этого утверждения:
 Говорят,
что функция
Говорят,
что функция
 выражена в виде суммы произведений
(конъюнкций) или в дизъюнктивной
нормальной форме. Например, терм АВ
является конъюнкцией двух переменных
А и
В
и, следовательно, называется конъюнктивным
термом.
выражена в виде суммы произведений
(конъюнкций) или в дизъюнктивной
нормальной форме. Например, терм АВ
является конъюнкцией двух переменных
А и
В
и, следовательно, называется конъюнктивным
термом.
Таким образом, в теореме утверждается, что в любой булевой функции, которая выражена в дизъюнктивной нормальной форме, конъюнкция, содержащая все переменные другой конъюнкции, является лишней. Это позволяет удалять лишние конъюнкции. Например, из функции
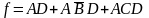
могут
быть удалены термы
 и ACD,
поскольку они содержат обе переменные,
присутствующие в AD.
Тогда функция примет вид f
= АD.
и ACD,
поскольку они содержат обе переменные,
присутствующие в AD.
Тогда функция примет вид f
= АD.
На рис. 1.13 приведена иллюстрация теоремы с помощью переключательных контактных схем. Очевидно, что наличие связи между точками Р u Q не зависит от того, замкнут или разомкнут переключатель В: следовательно, переключатель В лишний. Уравнение, двойственное по отношению к уравнению А = А + АВ, имеет вид А = А(А + В).
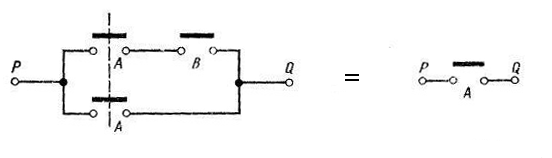 Переключательная
контактная схема, иллюстрирующая это
соотношение, приведена на рис. 1.14.
Переключательная
контактная схема, иллюстрирующая это
соотношение, приведена на рис. 1.14.
Рис. 1.13. Переключательные контактные схемы, иллюстрирующие теорему поглощения
А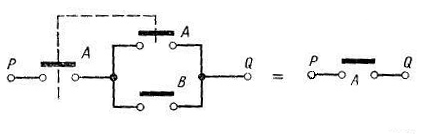 = А+АВ
= А+АВ
Рис. 1.14. Иллюстрация двойственной формы теоремы поглощения с помощью переключательных схем
