Часть b

1. Напишите уравнение прямой, проходящей через начало координат, которая параллельна касательной к графику функции 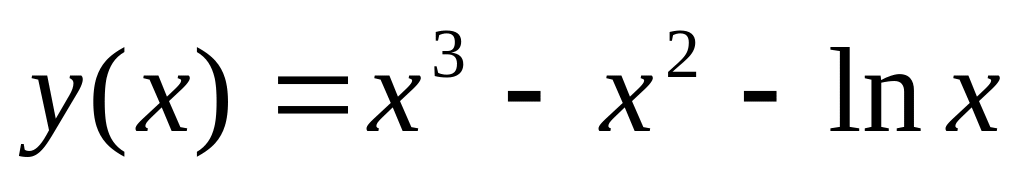, проведенной в точке .

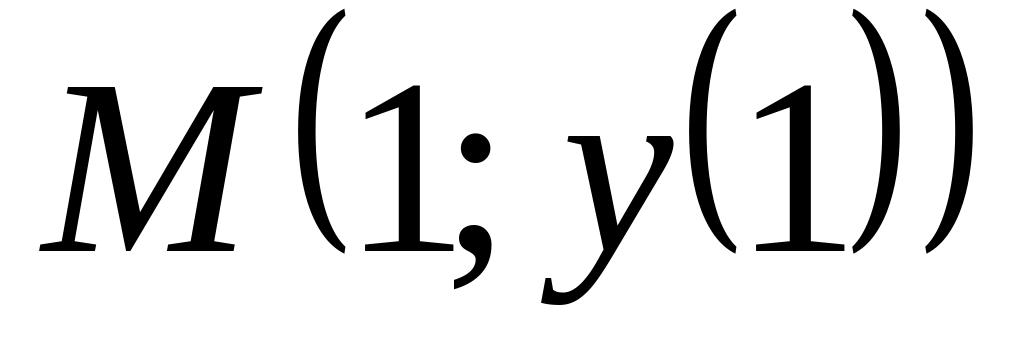Ответ: y=0

2. Напишите уравнение прямой, проходящей через начало координат, которая параллельна касательной к графику функции 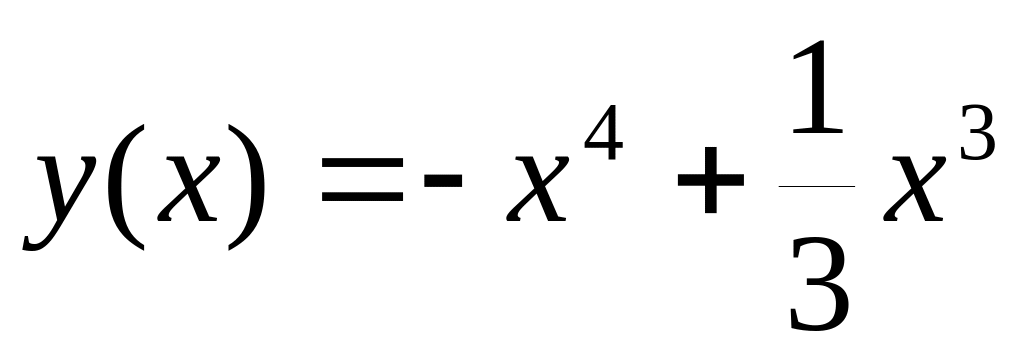, проведенной в точке .

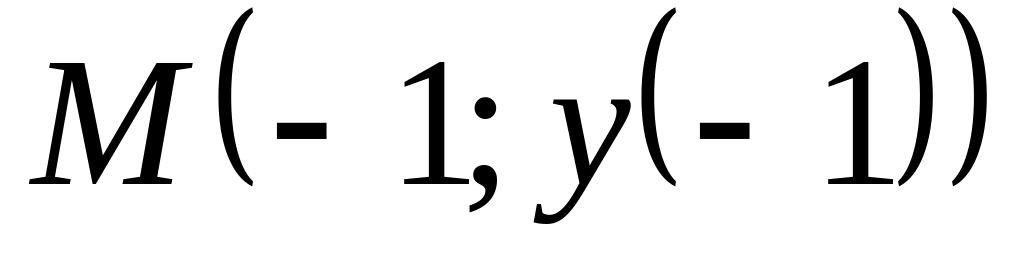Ответ: y=5x

3. Напишите уравнение прямой, проходящей через начало координат, которая параллельна касательной к графику функции 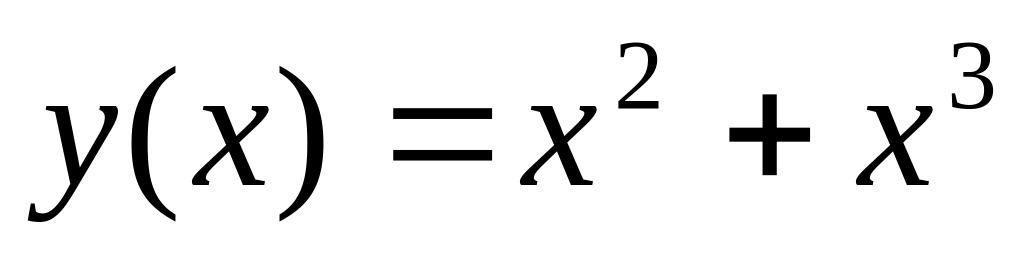, проведенной в точке .

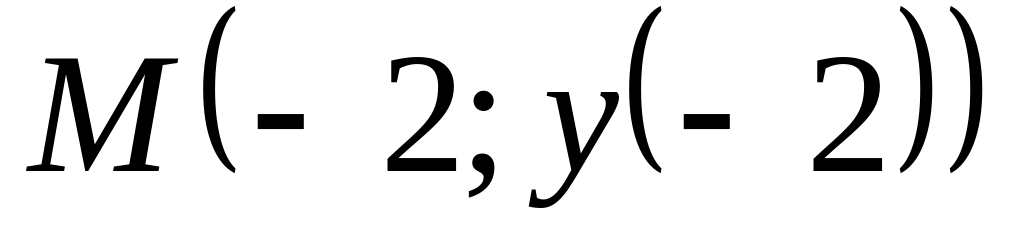Ответ: y=8x

4. На графике функци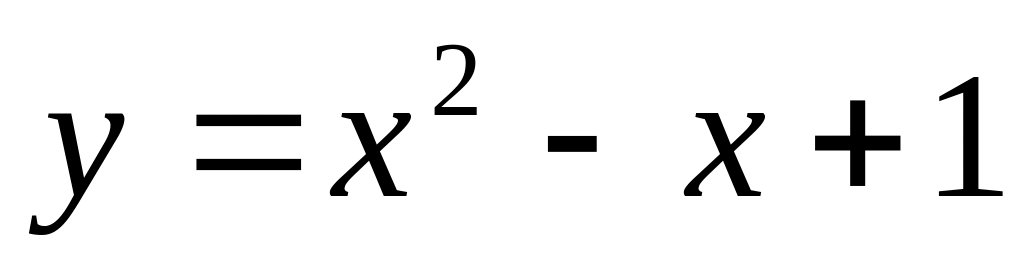и найдите точку М, в которой касательная к данному графику параллельна прямой .

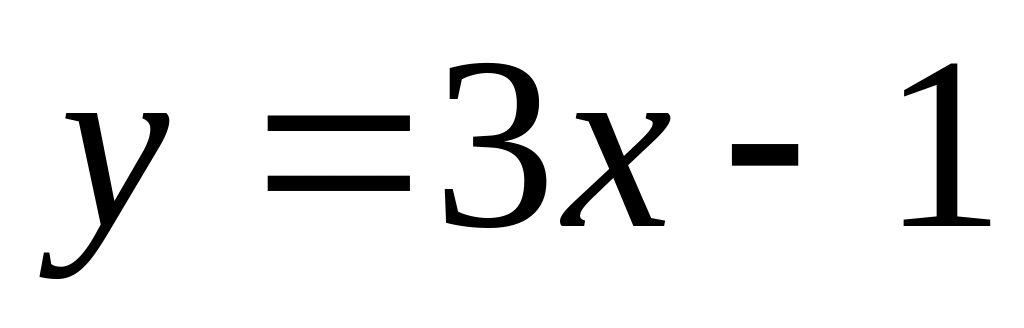Ответ: M(2;3)

5. На графике функци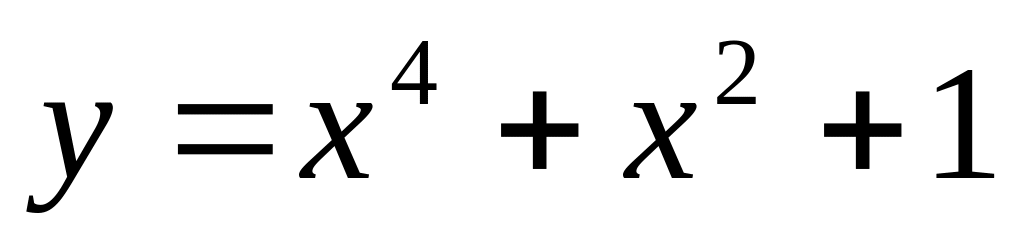и найдите точку М, в которой касательная к данному графику параллельна прямой .

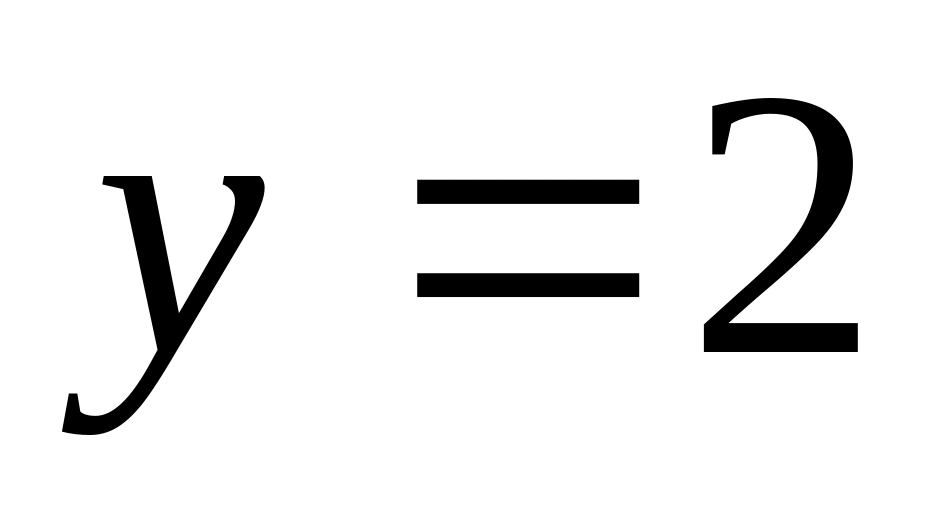Ответ: M(0;1)

6. Угол между диагональю прямоугольного параллелепипеда и плоского основания равен 30⁰. Найдите диагональ параллелепипеда, если стороны основания равны 2м и 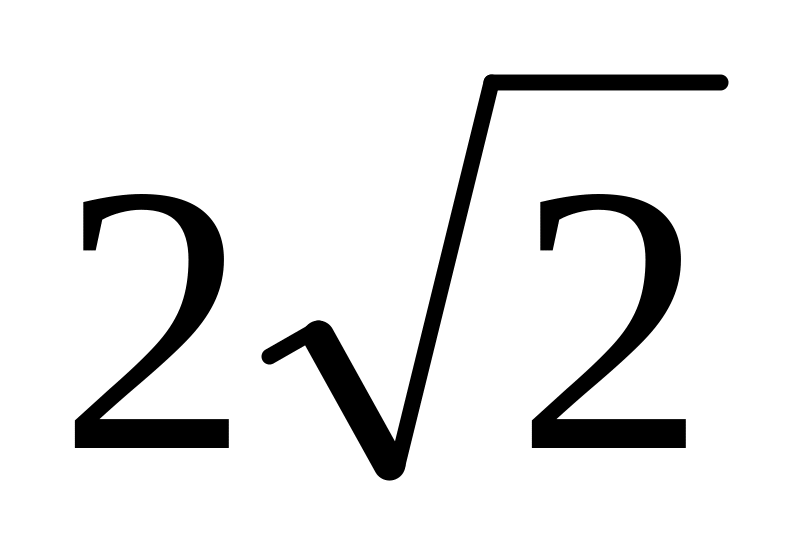м.

Ответ: 4

7. Сторона основания правильной четырехугольной призмы равна 4м, а диагональ боковой грани – 5м. Найдите объем призмы

Ответ: 48

8. Сторона основания правильной четырехугольной призмы равна 5м, а диагональ боковой грани – 13м. Найдите объем призмы.

Ответ: 300

9. Вычислите площадь фигуры, ограниченной линиями

y = x=0; x=3; y = 0.

Ответ: 13,5

10. Вычислите площадь фигуры, ограниченной линиями

y = x = 0; x = 3; y= 0.

Ответ: 21

11. Вычислить определённый интеграл

Ответ: 1

12. Найти площадь фигуры, заключённой между линиями: , осью ОХ и прямыми x=1 и x=5

Ответ: 160/9

13. Вычислить интеграл

Ответ:

14. Найти площадь фигуры, ограниченной прямыми: y=4/x; x=1; x=e; y=0.

Ответ: 4

15. Площадь поверхности куба равна 96 дм². Найти ребро куба (с точностью до 1 дм²).

Ответ: 4

16. Найти промежутки возрастания функции f(x) = x³ - 3x² +1

Ответ: (- )

17. Найти минимум функции f(x) = 2x³ - 9x² + 12x– 8

Ответ: -4

18. Найти промежутки выпуклости вверх графика функции y = x³ - 6x² + 2x– 6

Ответ: (- )

19. Найти точки перегиба графика функции y = x³ + 6x² + 9x + 8

Ответ: (-2; 6)

20. Найти промежутки выпуклости вниз графика функции y = x³ -3x²

Ответ: (1; )

Часть с

1. Представьте число 3 в виде суммы двух положительных слагаемых так, чтобы сумма утроенного первого слагаемого и куба второго слагаемого была наименьшей.

2. Представьте число 5 в виде суммы двух положительных слагаемых так, чтобы произведение первого слагаемого и куба второго слагаемого было наибольшим.

3. Огораживают спортивную площадку прямоугольной формы площадью2500м². Каковы должны быть ее размеры, чтобы на забор ушло наименьшее количество сетки «рабицы»?

4. Из шестиугольной призмы вырезали треугольную пирамиду, высота и площадь основания которой на 30 % и на 40% соответственно меньше высоты и площади основания призмы. Объем полученной пирамиды составляет от объема призмы

5.Исследовать и построить график функций y 2x³ x² 8x 7

6.Исследовать и построить график функций

7.Решить уравнение:

8.Вычислить площадь фигуры ограниченной графиками:

22