40.Критерий Дарбина-Уотсона.

Критерий Дарбина-Уотсона (или DW-критерий) — статистический критерий, используемый для нахождения автокорреляции остатков первого порядка регрессионной модели. Критерий назван в честь Джеймса Дарбина и Джеффри Уотсона. Критерий Дарбина-Уотсона рассчитывается по следующей формуле: где ρ₁ — коэффициент автокорреляции первого порядка. В случае отсутствия автокорреляции ошибок d = 2, при положительной автокорреляции d стремится к нулю, а при отрицательной стремится к 4: 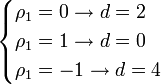На практике применение критерия Дарбина—Уотсона основано на сравнении величины d с теоретическими значениями d_L и d_U для заданного числа наблюдений n, числа независимых переменных модели k и уровня значимости α. Если d < d_L, то гипотеза о независимости случайных отклонений отвергается (следовательно присутствует положительная автокорреляция);  Если d > d_U, то гипотеза не отвергается;  Если d_L < d < d_U, то нет достаточных оснований для принятия решений.  Когда расчетное значение d превышает 2, то с d_L и d_U сравнивается не сам коэффициент d, а выражение (4 − d). Также с помощью данного критерия выявляют наличие коинтеграции между двумя временными рядами. В этом случае проверяют гипотезу о том, что фактическое значение критерия равно нулю. С помощью метода Монте-Карло были получены критические значения для заданных уровней значимости. В случае, если фактическое значение критерия Дарбина—Уотсона превышает критическое, то нулевую гипотезу об отсутствии коинтеграции отвергают. Недостатки: Неприменим к моделям авторегрессии.  Не способен выявлять автокорреляцию второго и более высоких порядков.  Даёт достоверные результаты только для больших выборок^].  Критерий h Дарбина применяется для выявления автокорреляции остатков в модели с распределёнными лагами: где n — число наблюдений в модели;  V — стандартная ошибка лаговой результативной переменной.  При увеличении объёма выборки распределение h-статистики стремится к нормальному с нулевым математическим ожиданием и дисперсией, равной 1. Поэтому гипотеза об отсутствии автокорреляции остатков отвергается, если фактическое значение h-статистики оказывается больше, чем критическое значение нормального распределения. Критерий Дарбина—Уотсона для панельных данных Для панельных данных используется немного видоизменённый критерий Дарбина—Уотсона: 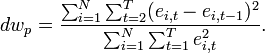В отличие от критерия Дарбина—Уотсона для временных рядов в этом случае область неопределенности является очень узкой, в особенности, для панелей с большим количеством индивидуумов.

41. Методы исключения автокорреляции (отклонений от тренда, последовательных разностей, включения фактора времени).

Сущность всех методов исключения тенденции заключается в том, чтобы устранить воздействие фактора времени на формирование уравнений временного ряда. Основные методы делят на 2 группы:

- основанные на преобразовании уровней ряда в новые переменные, не содержащие тенденции. Полученные переменные используем далее для анализа взаимосвязи изучаемых временных рядов. Эти методы предполагают устранение трендовой компоненты Т из каждого уровня временного ряда. 1.Метод последовательных разностей. 2.Метод отклонения от трендов.

- основанные на изучении взаимосвязей исходных уровней временных рядов при исключении воздействия фактора времени на зависимую и независимые переменные модели: включение в модель регрессии фактора времени.

Метод отклонений от тренда

Пусть имеются два временных ряда   и  , каждый из которых содержит трендовую компоненту Т и случайную компоненту  .

Проведение аналитического выравнивания по каждому из этих рядов позволяет найти параметры соответствующих уравнений трендов и определить расчетные по тренду уровни  и   соответственно. Эти расчетные значения можно принять за оценку трендовой компоненты Т каждого ряда. Поэтому влияние тенденции можно устранить путем вычитания расчетных значений уровней ряда из фактических. Эту процедуру проделывают для каждого временного ряда в модели. Дальнейший анализ взаимосвязи рядов проводят с использованием не исходных уровней, а отклонений от тренда   и  при условии, что последние не содержат тенденции.

 Метод последовательных разностей

В ряде случаев вместо аналитического выравнивания времен­ного ряда с целью устранения тенденции можно применить более простой метод — метод последовательных разностей.

Если временной ряд содержит ярко выраженную линейную тенденцию, ее можно устранить путем замены исходных уровней ряда цепными абсолютными приростами – первыми последовательными разностями.

Пусть  где  - случайная ошибка.

Тогда  

Коэффициент b — константа, которая не зависит от времени.  При наличии сильной линейной тенденции остатки   достаточно малы и в соответствии  с предпосылками МНК носят случайный характер. Поэтому первые разности уровней ряда   не зависят от переменной времени, их можно использовать для дальнейшего анализа.

Если временной ряд содержит тенденцию в форме параболы второго порядка, то для ее устранения можно заменить исходные уровни ряда на вторые разности.

Пусть имеет место соотношение   

Тогда:

  

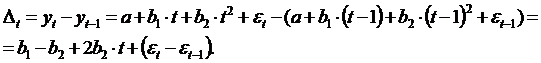
Как показывает это соотношение, первые разности   непо­средственно зависят от фактора времени t и, следовательно, со­держат тенденцию.

Определим вторые разности:

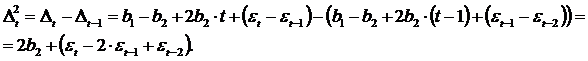
Очевидно, что вторые разности  не содержат тенденции, поэтому при наличии в исходных уровнях тренда в форме пара­болы второго порядка их можно использовать для дальнейшего анализа. Если тенденции временного ряда соответствует экспо­ненциальный или степенной тренд, метод последовательных раз­ностей следует применять не к исходным уровням ряда, а к их ло­гарифмам.

Включение в модель регрессии фактора времени

В корреляционно-регрессионном анализе устранить воздействие какого-либо фактора можно, если зафиксировать воздействие этого фактора на результат и другие включенные в модель факторы. Этот прием используется в анализе временных рядов, когда тенденция фиксируется через включение фактора времени в модель в качестве независимой переменной.

Модель вида   , относится к группе моделей, включающих фактор времени. Очевидно, что число независимых переменных в такой модели может быть больше единицы. Кроме того, это могут быть не только текущие, но и лаговые значения независимой переменной, а также лаговые значения результативной переменной. 

Преимущество данной модели по сравнению с методами отклонений от трендов и последовательных разностей в том, что она позволяет учесть всю информацию, содержащуюся в исходных данных, т.к  и   есть уровни исходных временных рядов. Кроме того, модель строится по всей совокупности данных за рассматриваемый период в отличие от метода последовательных разностей, который приводит к потере числа наблюдений. Параметры a и b модели с включением фактора времени определяются обычным МНК.