
- •Методы принятия оптимальных управленческих решений в экономике
- •Оглавление введение 6
- •1. Линейное программирование 9
- •2. Элементы теории игр 106
- •3. Контрольные задания 153
- •Заключение 198 Библиографический список 200 введение
- •1. Линейное программирование
- •1.1. Постановка задачи линейного программирования (злп)
- •Общая постановка задачи линейного программирования
- •Основная задача линейного программирования
- •Каноническая задача линейного программирования
- •1.2. Построение математических моделей экономических задач
- •Задачи планирования производства (задачи использования ресурсов)
- •Задачи о составлении рациона (или задачи о диете, о смесях)
- •Задачи о раскрое материалов (о минимизации отходов)
- •Задачи на использование мощностей оборудования
- •1.3. Графический метод решения злп
- •1.4. Решение злп симплексным методом
- •Опорное решение злп
- •Симплексный метод решения злп
- •Алгоритм симплекс-метода
- •Замечание об альтернативном плане
- •1.5. Метод искусственного базиса (метод больших штрафов)
- •1.6. Решение злп с помощью ms excel
- •1.7. Двойственность в линейном программировании Виды двойственных задач. Построение двойственных задач
- •Несимметричные двойственные задачи (стандартные формы)
- •Особенности составления несимметричных двойственных задач
- •Смешанные двойственные задачи
- •Теоремы двойственности. Нахождение двойственных оценок
- •Примеры составления двойственной задачи и нахождения двойственных оценок
- •Сформулируем экономико-математическую модель задачи.
- •Решим исходную задачу в ms Excel.
- •Отчет по результатам
- •Найдем оптимальный план двойственной задачи, используя теоремы двойственности.
- •Отчет по устойчивости
- •Выполним анализ на чувствительность полученного оптимального решения исходной задачи.
- •Найдем интервалы устойчивости для коэффициентов целевой функции и свободных членов системы ограничений.
- •Ответим на следующие вопросы, не прибегая к перерешиванию задачи:
- •1.8 Двойственный симплекс-метод
- •Алгоритм двойственного симплекс-метода
- •1.9 Транспортная задача линейного программирования
- •Методы составления первоначальных опорных планов
- •Проверка опорного плана на оптимальность. Метод потенциалов.
- •Переход к новому плану перевозок
- •2. Элементы теории игр
- •2.1. Основные понятия и классификация в теории игр
- •2.2. Решение матричных игр в чистых стратегиях Запись матричной игры в виде платёжной матрицы
- •Понятие о нижней и верхней цене игры. Решение игры в чистых стратегиях.
- •Уменьшение порядка платёжной матрицы
- •Пример решения матричной игры в чистых стратегиях
- •2.3. Смешанные стратегии в матричных играх Понятие о матричных играх со смешанным расширением
- •Решение игр размерности 2x2
- •Решение игр размерности 2 X n и m X 2
- •2.4. Решение матричных игр со смешанным расширением методами линейного программирования
- •2.5. Принятие решений в условиях неопределенности. Статистические игры. Понятие о статистических играх (играх с «природой»)
- •Критерии принятия решения
- •Пример решения статистической игры
- •Выручка от реализации капусты, тыс. Д.Е.
- •Определение экономического эффекта информации с использованием методов теории игр Основные факторы, определяющие величину эффекта прогноза состояний окружающей среды и значений выигрыша лпр
- •Задачи для самостоятельного решения.
- •3. Контрольные задания
- •Задача 1
- •Составьте математическую модель задачи и найдите
- •Решение, используя ms Excel.
- •Задача 2 Постройте математическую модель задачи и решите её симплексным методом.
- •Задача 3
- •Задача 5
- •Задача 6 Решите транспортную задачу.
- •Задача 7 Решите игру, предварительно проверив её на наличие седловой точки и по возможности максимально уменьшив размерность матрицы игры.
- •Задача 8 Запишите игровую модель задачи и найдите её решение в смешанных стратегиях.
- •Задача 9 Решите статистическую игру.
- •Задача 10 Решите задачу определения величины экономического эффекта информации.
- •Задание для курсовой работы на тему «Использование методов линейного программирования при выборе оптимального решения в розничной торговле»
- •Контрольные вопросы
- •Заключение
- •Библиографический список
Задачи для самостоятельного решения.
Фирма А производит некоторый сезонный товар, имеющий спрос в течение 3 лет, и который она может поставить на рынок в один из моментов i (i = 1, 2, 3).
Для конкурентной борьбы с фирмой А дочерняя фирма В концерна D, не заботясь о собственных доходах, производит аналогичный товар, который поступает на рынок в один из моментов j (j=1,2,3). Цель фирмы В - разорение фирмы А, после чего, используя капитал концерна D, она может легко наверстать упущенное. Единственным законным средством фирмы В в конкурентной борьбе является выбор момента поставки товара на рынок, так как понижение цены на поставляемый товар запрещено определенным соглашением. Для разорения фирмы А фирма В должна минимизировать ее доходы. Пусть технология выпуска товара такова, что чем дольше он находится в производстве, и, следовательно, позже поступает на рынок, тем выше его качество, а реализуется товар только более высокого качества (так как цена на товары разного качества одна и та же). Доход от продажи товара в единицу времени составляет 4 денежных единиц.
Требуется построить матрицу выигрышей фирмы А, где под выигрышем понимается в данном случае доход этой фирмы, зависящий от складывающихся ситуаций. Используя полученную матрицу игры, найти все оптимальные стратегии обоих игроков. Предварительно проверить наличие седловой точки и возможности доминирования.
В конфликтной ситуации участвуют две стороны: А - государственная налоговая инспекция; В – налогоплательщик с определенным годовым доходом, налог с которого составляет 13 % годовых.
У стороны А два возможных варианта поведения. А1 – не контролировать доход налогоплательщика; А2 – контролировать доход налогоплательщика В и взимать с него:
- налога в размере 13 % годовых, если доход заявлен и соответствует действительности;
- налога в размере 13 % годовых и штрафа в размере 7%, если заявленный в декларации доход меньше действительного, или в случае сокрытия всего налога.
У стороны В три стратегии поведения: В1 – заявить о действительном доходе; В2 – заявить доход меньше действительного и реально налог в этом случае составит 7%; В3 – скрыть доход, тогда не надо будет платить налог.
Составить матрицу игры и найти все оптимальные стратегии обоих игроков. Предварительно проверить наличие седловой точки и возможности доминирования.
Доминировать матрицу игры:
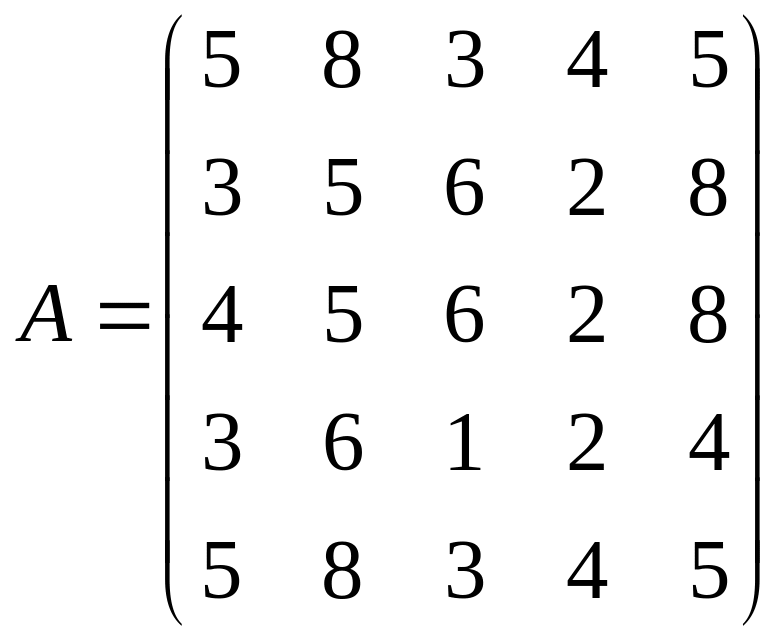 .
.
Найти верхнюю и нижнюю цену игры, максиминные и минимаксные стратегии игроков.
Решить графически игру, заданную матрицей:
 .
.Требуется найти оптимальные стратегии первого игрока в игре с природой в условиях полной неопределённости, используя все известные критерии. Уровень пессимизма принять 0,6. Дать обоснованные рекомендации игроку А. Матрица игры с природой в условиях полной неопределённости задана следующая:
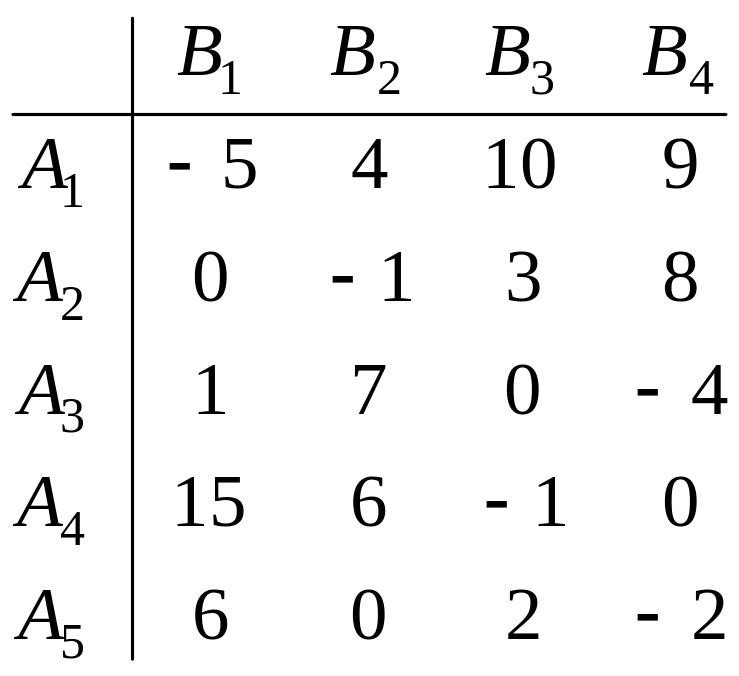 .
.
Решить эту же игру в условиях риска, если известны вероятности состояний природы:
![]() .
.
Уровень достоверности информации о вероятностях состояний природы принять u = 0,7.
Ответы:
Матрица игры
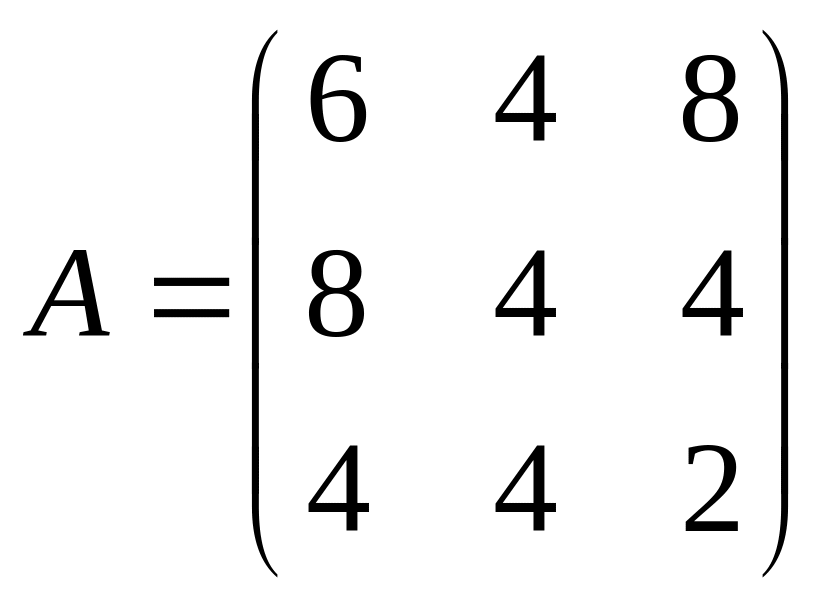 .
В игре есть две седловые точки: (А1,В2)
и (А2.В2). То есть, фирме А
нужно выходить на рынок в 1 или 2 год, а
фирме В во второй год. Цена игры
= 4 денежным единицам.
.
В игре есть две седловые точки: (А1,В2)
и (А2.В2). То есть, фирме А
нужно выходить на рынок в 1 или 2 год, а
фирме В во второй год. Цена игры
= 4 денежным единицам.Матрица игры
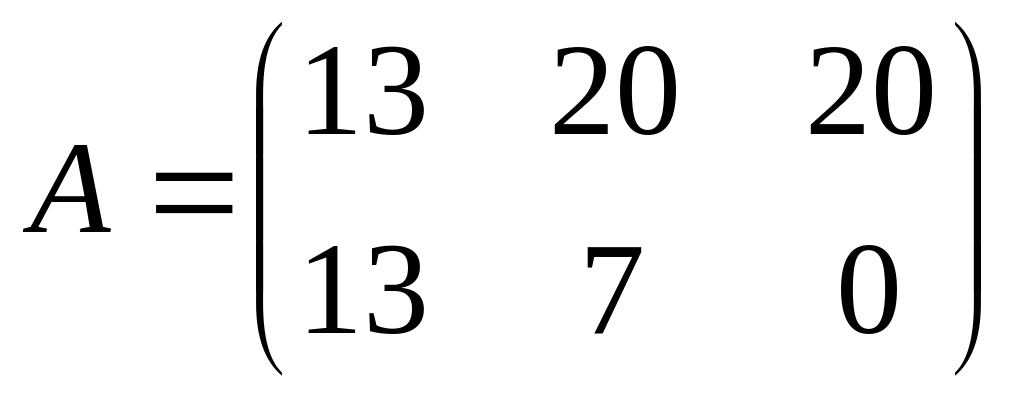 .
В игре есть седловая точка: (А1,В1).
То есть, налоговой инспекции необходимо
придерживаться первой стратегии, т.е.
контролировать доходы налогоплательщика,
а налогоплательщику – заявлять истинный
доход. Цена игры
= 13 %.
.
В игре есть седловая точка: (А1,В1).
То есть, налоговой инспекции необходимо
придерживаться первой стратегии, т.е.
контролировать доходы налогоплательщика,
а налогоплательщику – заявлять истинный
доход. Цена игры
= 13 %.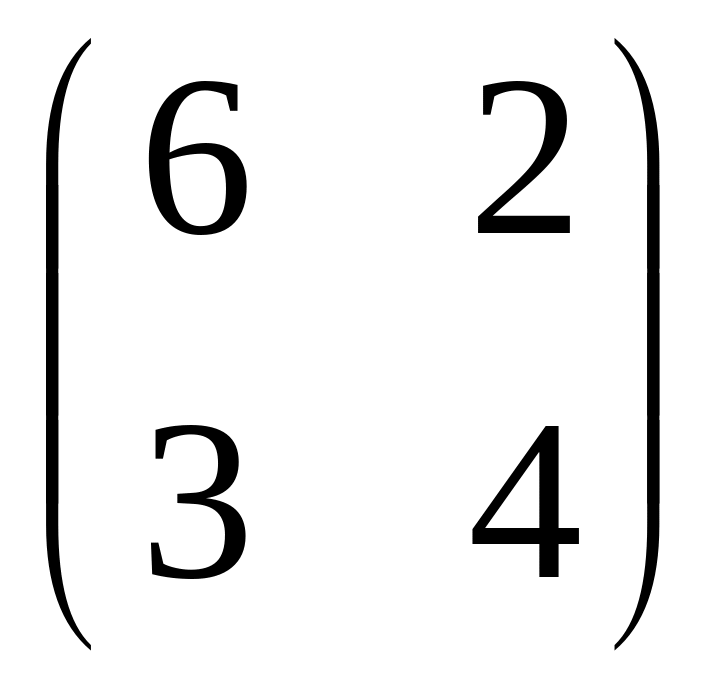 .
Нижняя цена игры
=3
и соответствующая максиминная стратегия
первого игрока А5; верхняя цена
игры
=
4 и соответствующая минимаксная стратегия
второго игрока В4.
.
Нижняя цена игры
=3
и соответствующая максиминная стратегия
первого игрока А5; верхняя цена
игры
=
4 и соответствующая минимаксная стратегия
второго игрока В4.Р*(0; 0,5; 0; 0; 0,5), Q*(0,5; 0,5), =4.
По критерию Вальда – А2 или А4; по критерию Сэвиджа – А4 или А5; по критерию максимакса - А4; по критерию Гурвица с уровнем пессимизма 0,6 - А4; по критерию Байеса – А1; по критерию Лапласа - А4; по критерия Ходжа – Лемана с уровнем достоверности информации о вероятностях состояний природы u = 0,7 – А1.
