1.8 Двойственный симплекс-метод

Ранее было рассмотрено (п. 1.3), как с помощью симплекс-метода можно получить решение задачи линейного программирования, предварительно приведя её к канонической форме (задача 1.18).

Двойственный симплекс-метод можно применять при решении задачи линейного программирования, свободные члены системы уравнений которой не обязаны быть неотрицательными (как в задаче 1.18), ( ), т.е. могут быть любыми числами.

, (1)

Применив к системе (1) метод Жордана – Гаусса, можно привести её к виду:

(2)

где - базисные переменные, а - свободные переменные и - любого знака. Выразив базисные переменные через свободные, получим общее решение системы ограничений (2):

.

Однако это решение не является планом задачи (1), т.к. среди его компонент имеются отрицательные числа.

Определение 1.

Решение системы линейных уравнений (2) называется псевдопланом задачи (1), если

для любого j (j=l,n).

Теорема 1.9 (признак отсутствия оптимального плана)

Если в псевдоплане есть хотя бы одно отрицательное число b_i<0 такое, что все ≥ 0 ( ), то задача (1) вообще не имеет планов.

Теорема 1.10

Если в псевдоплане имеются отрицательные числа b_i<0, такие, что для любого из них существуют числа <0, то можно перейти к новому псевдоплану, при котором значение целевой функции задачи (1) не уменьшится.

Сформулированные теоремы дают основание для построения алгоритма двойственного симплекс-метода.

Алгоритм двойственного симплекс-метода

1. Получение первоначального опорного плана задачи. Для этого систему ограничений исходной задачи требуется привести к системе неравенств смысла «≤». Для этого обе части неравенства смысла «≥» необходимо умножить на (-1). Затем от системы неравенств смысла «≤» перейти к системе уравнений, вводя неотрицательные дополнительные переменные, которые являются базисными переменными. Первый опорный план заносят в симплексную таблицу.

2. Проверка опорного плана на оптимальность. Если в полученном опорном плане не выполняется условие оптимальности ( 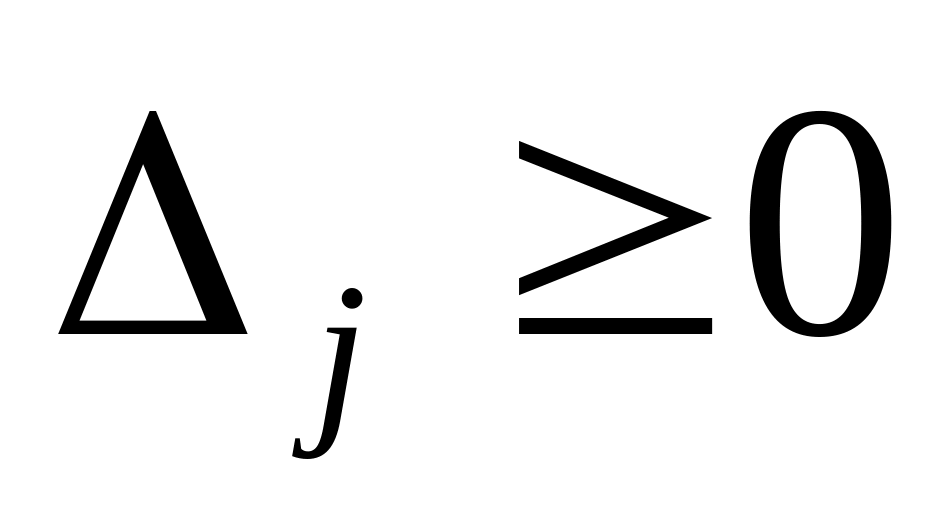), то следует решать задачу симплексным методом. При этом в столбце b_i / a_ik отношения считают только в случае одноименных знаков b_i и a_{ik .} В противном случае значения b_i / a_ik не определяют.

Если в опорном плане условия оптимальности удовлетворяются и все значения базисных переменных – положительные числа, то получен оптимальный план. Наличие отрицательных значений в столбце b_i свидетельствует о получении псевдоплана.

3. Если среди b_i нет отрицательных, то получен оптимальный план задачи. В противном случае устанавливается неразрешимость задачи по теореме 1.9, либо осуществляется переход к новому псевдоплану.

4. Выбирают разрешающую строку с помощью определения наибольшего по абсолютной величине отрицательного числа столбца свободных членов.

Симплексную таблицу дополняют строкой , в которую заносят взятые по абсолютной величине результаты деления симплексных разностей на отрицательные коэффициенты разрешающей строки. Минимальные значения  определяют разрешающий столбец и переменную, вводимую в базис. На пересечении разрешающей строки и разрешающего столбца находится разрешающий элемент.

5. Находят новый псевдоплан методом Жордана - Гаусса и повторяют все действия начиная с этапа 3.

Рассмотрим работу двойственного симплекс-метода на примере.

Пример 13. Известно, что содержание трех питательных веществ A, B и C в рационе должно быть не менее 60, 50 и 12 единиц соответственно. Указанные питательные вещества содержат три вида продуктов. Содержание единиц питательных веществ в одном килограмме каждого из видов продукта приведено в таблице 1.10.

Определить дневной рацион, обеспечивающий получение необходимого количества питательных веществ при минимальных денежных затратах.

Таблица 1.10

Питательные вещества	Количество единиц питательных веществ в 1 кг продукта вида
	I	II	III
A	1	3	4
B	2	4	2
C	1	4	3
Цена 1 кг продукта	9	12	10

Составим экономико-математическую модель задачи. Обозначим x₁, x₂, x₃ – объемы продуктов (кг) в рационе. Необходимо определить вектор обеспечивающий минимум целевой функции :

и удовлетворяющий следующим условиям:

Решение. Запишем исходную задачу линейного программирования в форме основной задачи: найти максимум функции при условиях

Приведем систему ограничений к системе неравенств смысла «≤», умножив обе части неравенства на (-1).

Составим для последней задачи двойственную. Такой является задача, в результате решения которой требуется найти минимальное значение функции

Решим исходную задачу. Перейдем к системе уравнений, вводя дополнительные переменные:

Пусть - базисные переменные, а - свободные переменные. Полагая , получим первый опорный план Занесем данный план в первую симплекс таблицу 1.11.

План двойственной задачи можно найти по симплекс-таблице по следующей формуле:

где j – номер базисной переменной начального опорного решения.

Из этой таблицы видим, что планом двойственной задачи является .

Таблица 1.11

i	Базис	С баз	-9	-12	-10	0	0	0	bi
1		0	-1	-3	-4	1	0	0	-60
2		0	-2	-4	-2	0	1	0	-50
3		0	-1	-4	-3	0	0	1	-12
4			9	12	10	0	0	0	0
5	j		9	4	2,5	-	-	-

Так как среди оценок нет отрицательных, а b_i<0 для i=1,2,3, то план в симплексной таблице является псевдопланом.

В соответствии с алгоритмом двойственного симплекс-метода переходим к новой симплекс-таблице. (В данном случае это мож­но сделать, так как в строках, соответствующих отрицательным правым частям имеются отрица­тельные числа. Если бы они отсутствовали хотя бы в одной из строк, то задача была бы неразрешима.) Вектор, исключаемый из базиса, определяется наибольшим по абсолютной величине отрицательным числом, стоящим в столбце вектора свободных членов. В данном случае это число -60, т.к. . Следовательно, 1-я строка симплексной таблицы является разрешающей, а переменную следует вывести из базиса. Для определения разрешающего столбца дополним симплексную таблицу строкой  , в которую внесем величины _j = , где <0 для свободных переменных: ₁ = =9, ₂ = =4, ₃ = =2,5. По min _j = , где <0 определяют переменную, которую необходимо ввести в базис на следующем шаге. Минимальное значение _j равно 2,5 и соответствует переменной x₃. Таким образом, переменную x₃ следует ввести в базис, а третий столбец будет разрешающим. На пересечении разрешающей строки и разрешающего столбца находится разрешающий элемент, равный -4.

Далее выполняем преобразования методом Жордана - Гаусса и заполняем симплексную таблицу 1.12.

Таблица 1.12

i	Базис	С баз	-9	-12	-10	0	0	0	bi
1		-10	0,25	0,75	1	-0,25	0	0	15
2		0	-1,5	-2,5	0	-0,5	1	0	-20
3		0	-0,25	-1,75	0	-0,75	0	1	33
4			6,5	4,5	0	2,5	0	0	-150
5	j		13/3	1,8	-	5	-	-

Получаем план , который также является псевдопланом. Из этой таблицы видим, что планом двойственной задачи является .

От плана по вышеизложенному алгоритму переходим к плану , представленному в таблице 1.13.

Таблица 1.13

i	Базис	С баз	-9	-12	-10	0	0	0	bi
1		-10	-0,7	0	1	-0,4	0,3	0	9
2		-12	0,6	1	0	0,2	-0,4	0	8
3		0	0,8	0	0	-0,4	-0,7	1	47
4			3,8	0	0	1,6	1,8	0	-186

Последний опорный план является оптимальным, так как все симплекс-разности неотрицательны и все значения базисных переменных положительны.

Таким образом .

Оптимальным планом двойственной задачи является .

Учитывая, что исходная задача состояла в отыскании минимального значения целевой функции, сделаем переход и запишем ответ задачи.

Ответ: .

Пример 14. Найти максимальное значение функции

при условиях

Решение. Запишем исходную задачу линейного программирования в форме основной задачи: найти максимум функции при условиях

Умножим второе и третье уравнения системы ограничений последней задачи на -1, и переходим к следующей задаче: найти максимум функции

при условиях

Составим для последней задачи двойственную. Такой является задача, в результате решения которой требуется найти минимальное значение функции

(3)

Выбрав в качестве базисных векторов, вектора при переменных , составим симплексную таблицу (табл. 1.10) для исходной задачи (1).

Таблица 1.10

I	Базис	С баз	1	1	2	0	0	bi
1		2	1	1	1	0	0	8
2		0	-1	1	0	1	0	-4
3		0	-1	-2	0	0	1	-6
4			1	1	0	0	0	16
5	j		1	1/2	-	-	-

Из этой таблицы видим, что планом двойственной задачи (3) является У= (2; 0; 0;). При этом плане Z = 16.

Так как в столбце вектора свободных членов табл. 1.10 имеются два отрицательных числа (-4 и -6), а в 4-й строке отрицательных чисел нет, то в соответствии с алгоритмом двойственного симплекс-метода переходим к новой симплекс-таблице. (В данном случае это мож­но сделать, так как в строках, соответствующих отрицательным правым частям имеются отрица­тельные числа. Если бы они отсутствовали в одной из строк, то задача была бы неразрешима.) Вектор, исключаемый из базиса, определяется наибольшим по абсолютной величине отрицательным числом, стоящим в столбце вектора свободных членов. В данном случае это число -6. Следовательно, из базиса исключаем переменную . Чтобы определить, какую переменную необходимо ввести в базис, находим

min _j = , где <0.

В данном случае в базис вводим переменную . Переходим к новой симплекс-таблице (табл. 1.11).

Таблица 1.11

i	Базис	С баз	1	1	2	0	0	bi
1		2	1/2	0	1	0	1/2	5
2		0	-3/2	0	0	1	1/2	-7
3		1	1/2	1	0	0	-1/2	3
4			1/2	0	0	0	1/2	13
5	j		1/3	-	-	-	-

Из этой таблицы видно, что получен новый план двойствен­ной задачи У= (2; 0; 1/2). При этом плане значение ее линейной формы равно Z = 13. Таким образом, с помощью алгоритма двойственного симплекс-метода произведен упорядоченный пе­реход от одного плана двойственной задачи к другому.

Так как в столбце вектора свободных членов табл. 1.11 стоит отрицательное число -7, то рассмотрим элементы 2-й строки. Среди этих чисел есть одно отрицательное -3/2. Если бы такое число отсутство­вало, то исходная задача была бы неразрешима. Таким образом, в базис вводится новая переменная x₁ вместо x₄. В данном случае переходим к новой симплекс-таблице (табл. 1.12)

Таблица 1.12

i	Базис	С баз	1	1	2	0	0	bi
1		2	0	0	1	1/3	2/3	8/3
2		1	1	0	0	-2/3	-1/3	14/3
3		1	0	1	0	1/3	-1/3	2/3
4			0	0	0	1/3	2/3	32/3

Как видно из табл. 1.12, найдены оптимальные планы исход­ной и двойственной задач. Ими являются Х*= (14/3; 2/3; 8/3) и У*= (2; 1/3; 2/3). При этих планах значения линейных целевых функций исходной и двойственной задач равны: F_max = Z_min = 32/3.

Пример 15. Найти максимальное значение функции

при условиях

Решение. Умножая первое и третье уравнения системы ограничений задачи на -1, в результате приходим к задаче на­хождения максимального значения функции при условиях

Взяв в качестве базисных переменных , составляем симплекс-таблицу (табл. 1.13).

Таблица 1.13

i	Базис	С баз	2	3	0	5	0	bi
1		0	2	-1	1	0	0	-12
2		5	1	2	0	1	0	10
3		0	-3	2	0	0	1	-18
4			30	7	0	0	0	50
5	j		-	7	-	-	-

В 4-й строке табл. 1.13 нет отрицательных чисел. Следова­тельно, если бы в столбце вектора свободных членов не было отрицательных чисел, то в табл. 1.13 был бы записан оптимальный план. По­скольку в указанном столбце отрицательные числа имеются и такие же числа содержатся в соответствующих строках, пере­ходим к новой симплекс-таблице (табл. 1.14). Для этого исклю­чим из базиса переменную и введем в базис переменную . В результате получим псевдоплан X =(6; 0; -24; 4; 0).

Таблица 1.14

i	Базис	С баз	2	3	0	5	0	bi
1		0	0	1/3	1	0	2/3	-24
2		5	0	8/3	0	1	1/3	4
3		2	1	-2/3	0	0	-1/3	6
4			0	9	0	0	1	32

Так как в строке, соответствующей -24, нет отрицательных чисел, то исходная задача не имеет решения.