16 Вертикальные нагрузки от сил инерции

необрессоренных масс определяют по 2-му закону Ньютона, как произведение массы элемента колесной пары на ускорение.

При этом в качестве расчетного принимается наиболее неблагоприятное условие несимметричного действия инерционных сил.

Например, на левом колесе оно возникает, а на правом – отсутствует. На основе обработки экспериментальных замеров ускорений установлена эмпирическая формула зависимости ускорения буксового узла от скорости движения вагона

,

где D – величина, зависящая от типа вагона, определяемая по выше приведенной таблице.

– сумма масс необрессоренных частей вагона, опирающихся на рельс:

,

где , , – массы колесной пары, буксового узла и необрессоренных деталей, опирающихся на буксу.

Для расчетной схемы, приведенной на схеме г, может быть принят линейный закон изменения ускорения вдоль оси колесной пары. Если вертикальное ускорение левого колеса этой схемы вычислять по формуле (5.16), то для ускорения средней части оси и правого буксового узла справедливы формулы

,

.

Силы инерции, действующие на шейки оси (схема г):

– левую – ;

– правую – ,

где , – суммы необрессоренных масс, приходящихся на левую и правую шейки оси соответственно.

Сила инерции левого колеса

.

Средней части оси

,

где , – массы соответственно колеса и средней части оси. Сила приложена на расстоянии от плоскости круга катания левого колеса.

Вертикальные реакции рельсов от действия инерционных сил определяются условиями равновесия

откуда

.

Из условия можно получить выражение

Рассмотрение возможных комбинаций активных и реактивных нагрузок показывает, что при самом неблагоприятном сочетании сил к центрам шеек будут приложены вертикальные расчетные нагрузки (для схем а) – г)).

К левой:

;

К правой:

.

Соответствующие вертикальные реакции рельсов определяются по формулам:

Левого колеса:

Правого колеса:

17 Нагруженность расчетных сечений оси

Вычисленные выше усилия, действующие на элементы колесной пары, позволяют перейти к оценке прочности ее оси. Она имеет переменные по длине сечения, причем размеры оси, точнее площади сечения, подобраны из условия равнопрочности ее различных зон.

Схема осевого сечения оси колесной пары

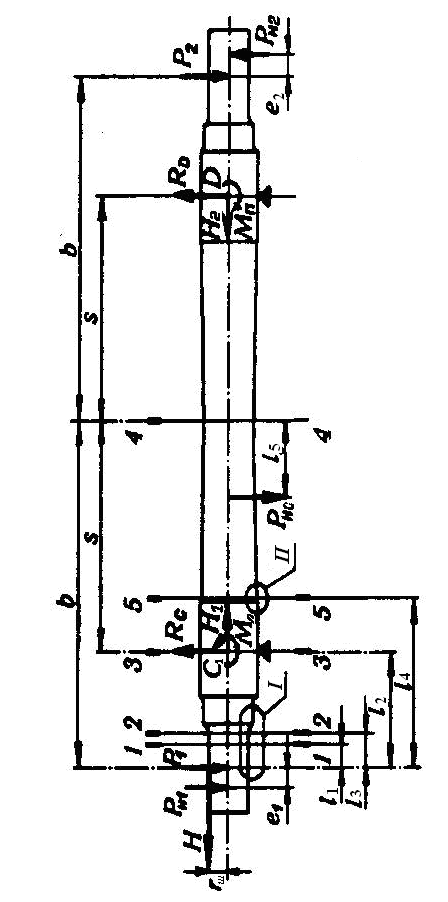
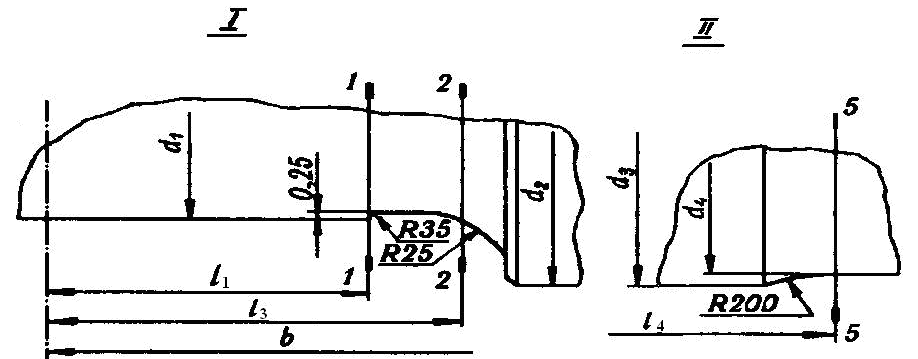
Цифрами 1–1, 2–2,…,5–5 на приведенной схеме обозначены расчетные сечения оси, внутренние сечения в которых могут привести в эксплуатационных условиях к ее разрушению. Основной причиной разрушения при этом является появление усталостных трещин и их последующие развитие в условиях действия циклически изменяющихся знакопеременных нормальных напряжений.

Перечислим наиболее загруженные сечения оси:

1–1 – по внутренней кромке кольца заднего роликового подшипника у начала разгружающей канавки;

2–2 – по внутренней галтели шейки на расстоянии 1/3 длины переходного участка от начала галтели;

3–3 – в плоскости круга катания;

4–4 – посередине оси;

5–5 – по галтели вместе перехода от подступичной к средней части оси.

Изгибающие моменты, возникающие в оси колесной пары, определяются внешними нагрузками на ось, а также реакциями со стороны рельсового пути в процессе движения. Эти моменты вычисляются по формулам (соответственно по сечениям 1-1,…,5-5 и размерам, представленным на схеме оси):

Замечание: В расчетной схеме оси колёса представлены силами Н₁ и Н₂, а так же изгибающими моментами М_л и М_п, определяемыми по формулам

,

где  – коэффициент передачи инерционных нагрузок на внутренние сечения оси;  = 0,7;

r – радиус подступичной поверхности; r = d₄/2.

Изгибающие моменты в сечениях 1-1,…, 5-5 от вертикальной статической нагрузки определяются равенствами

где Р_ст – статическое усилие от веса вагона, воспринимаемое шейкой вагонной оси. Формула для него приводилась раньше.

Моменты сопротивления изгибу расчетных сечений i = 1,2,…,5 определяется по формулам:

для сплошной оси

для полой оси

где d_i – наружный диаметр оси в i-ом расчетном сечении, м.

d_oi – диаметр полости в i-ом расчетном сечении, м.

Величины нормальных осевых (для оси колесной пары) напряжений, возникающие от действия описанных усилий и моментов вычисляются с помощью равенства

Замечание: Напряжения, определяемые по формуле (6.1) учитывают неблагоприятно сечение различных нагрузок, возникающих при движении поезда. Их не следует смешивать с напряжениями, возникающими в сечениях вагонной оси, от статической нагрузки

(6.2)

При оценке прочности вагонной оси учитываются оба из указанных видов напряжений.