35 Расчет резиновых элементов рессорного подвешивания
Назначение резиновых элементов рессор:
1. Обеспечение необходимой податливости;
2. Гашение колебаний.
Особенность: модуль продольной упругости резины при статической нагрузке значительно отличается от значения модуля при динамическом нагружении. Поэтому расчет резиновых элементов рессоры производится отдельно для статических и для динамических нагрузок.
Значение модуля определяется, как правило косвенно – по ее твердости. При этом используется формула:
,
где
– твердость
резины по Шору, определяемая
экспериментально. Формула (9.17) применима
для
единиц твердости.
Расчетный статический
модуль упругости сжатия
зависит от формы амортизатора.
Соответствующий коэффициент формы
определяется равенством:
,
(9.18)
где
,
– площади
нагружения и выпучивания упругого
элемента.
Поясним введенные понятия примером.
Рассмотрим сжатие цилиндрического резинового элемента.
Для приведенной
схемы нагружения:
.
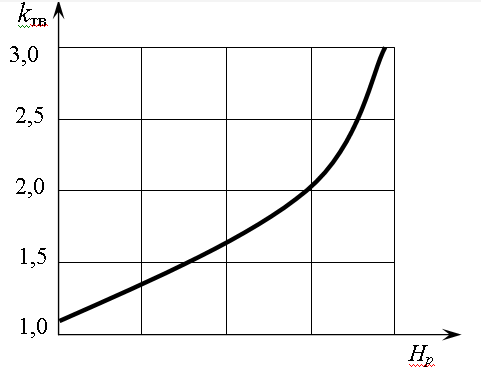
Кривые линии на приведенном рисунке относятся к различным сортам резины, имеющим различную твердость .
Модуль упругости при динамическом нагружении резины увеличивается вместе с ее твердостью и рассчитываются по формуле
(9.20)
где
–
коэффициент увеличивающийся с увеличением
твердости резины Нр
Различают резиновые амортизаторы, работающие на сжатие (амортизаторы сжатия), на сдвиг и на сжатие-сдвиг. Для амортизатора сжатия напряжения сжатия определяются по формуле
,
где – осадка амортизатора;
– исходная высота
амортизатора.
Для применимости формулы (9.21) необходимо, что бы относительные деформации не превышали 20%. При большей степени сжатия формула (9.21) требуют уточнения. Если нагрузка Р на амортизатор известна, то напряжения по определению удовлетворяет соотношению
,
где F – площадь поперечного сечения амортизатора.
Приравнивая правые части (9.21) и (9.22) получаем
;
Отсюда можно определить жесткость амортизатора и его гибкость λ
;
.
Формулы (9.24) соответствует упругому элементу амортизатора, опорная часть (основание) которого закреплено в вертикальном направлении, но свободно в поперечном. В случае если это основание жестко закреплено в поперечном направлении, это может быть учтено специальным коэффициентом увеличения жесткости.
Для резиновых элементов рессор, работающих на сдвиг, угловые деформации сдвига γ считаются малыми, если выполняется соотношение:
Используя равенство (9.24) приходим к соотношению для касательных напряжений τ
Одновременно для величины τ можем записать
Приравнивая равные части последних равенств, получаем
;
;
(9.28)
При расчете резиновых элементом амортизаторов, работающих на сжатие со сдвигом используется расчетная схема,
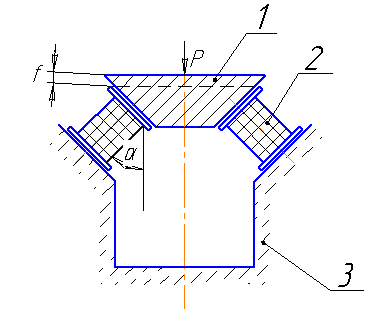
1 – надрессорная часть упругого резинового элемента рессоры; 2 – упругий резиновый элемент рессоры; 3 – ненадрессорная часть упругого элемента рессоры.
представленная на рисунке.
Жесткость упругого элемента определяется в этом случае по формуле, вытекающей как и в предыдущих случаях, из условия равновесия сил упругости деформированного резинового элемента и внешней расчетной силы тяжести вагона, рассмотренных в проекции на вертикальное направление
где величины F, h, G, E аналогичны характеристикам, входящим в предыдущие формулы (9.17) – (9.28), а α – угол отклонения амортизатора от вертикали, соответствующий рассматриваемой схеме его деформирования. Из формулы (9.29) следует, что при α = 0 – эта формула совпадает с формулой (9.24) для деформации элемента, работающего на сжатие. При α = π/2 – соотношение (9.29) переходит в формулу (9.28) для амортизатора, работающего на сдвиг.