Вопрос №4 Специальные бинарные отношения

В математике важную роль играют два вида специальных бинарных отношений: отношение эквивалентности и отношение порядка.

Отношение эквивалентности ( ) на множестве   — это бинарное отношение, для которого выполнены следующие условия:

1. Рефлексивность: 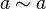  для любого 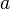  в  ,

2. Симметричность: если 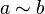 , то  ,

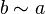3. Транзитивность: если   и 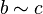 , то  .

Запись вида « » читается как «  эквивалентно  ».

Классом эквивалентности   элемента   называется подмножество элементов, эквивалентных  . Из вышеприведённого определения немедленно следует, что, если  , то  .

Фактормножество — множество всех классов эквивалентности заданного множества   по заданному отношению  , обозначается  .

Для класса эквивалентности элемента   используются следующие обозначения:  ,  ,  .

Множество классов эквивалентности по отношению   является разбиением множества.

Бинарное отношение   на множестве   называется отношением нестрогого частичного порядка (отношением порядка, отношением рефлексивного порядка), если имеют место

• Рефлексивность: 

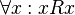
• Антисимметричность:  .

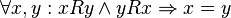• Транзитивность:  ;

Множество  , на котором введено отношение частичного порядка, называется частично упорядоченным. Отношение нестрогого частичного порядка часто обозначают знаком 

Варианты

Отношение частичного порядка   называется линейным порядком, если выполнено условие Множество  , на котором введено отношение линейного порядка, называется линейно упорядоченным, или цепью.

Отношение  , удовлетворяющее только условиям рефлексивности и транзитивности, называется квазипорядком, или предпорядком.

Вопрос№6 Отношения порядка

Бинарное отношение   на множестве   называется отношением нестрогого частичного порядка (отношением порядка, отношением рефлексивного порядка), если имеют место

• Рефлексивность: 

• Антисимметричность:  .

• Транзитивность:  ;

Множество  , на котором введено отношение частичного порядка, называется частично упорядоченным. Отношение нестрогого частичного порядка часто обозначают знаком 

Варианты

Отношение частичного порядка   называется линейным порядком, если выполнено условие

Множество  , на котором введено отношение линейного порядка, называется линейно упорядоченным, или цепью.

Отношение  , удовлетворяющее только условиям рефлексивности и транзитивности, называется квазипорядком, или предпорядком.

Вопрос № 7 Свойства операций над множествами: дистрибутивность, законы де Моргана и диаграммы Эйлера-Венна

Дистрибути́вность (от лат. distributivus — «распределительный»), также распределительный закон^[1] — свойство согласованности двух бинарных операций, определённых на одном и том же множестве.

Говорят, что две бинарные операции + и × удовлетворяют свойству дистрибутивности, если для любых трех элементов  :

 — дистрибутивность слева;

 — дистрибутивность справа.

Если операция × является коммутативной, то свойства дистрибутивности слева и справа совпадают.

Аддитивная и мультипликативные операции в кольцах и полях по определению удовлетворяют свойству дистрибутивности.

Если операции сложения и пересечения для односторонних идеалов некоторого кольца (или подмодулей некоторого модуля) удовлетворяют свойству дистрибутивности, то говорят о дистрибутивном кольце (или дистрибутивном модуле).

Законы де Мо́ргана (правила де Мо́ргана) — логические правила, связывающие пары логических операций при помощи логического отрицания. Открыты шотландским математиком Огастесом де Морганом

Теорема

Если существует операция логического умножения двух и более элементов, операция «и» — (A&B), то для того, чтобы найти обратное от всего суждения ~(A&B), необходимо найти обратное от каждого элемента и объединить их операцией логического сложения, операцией «или» — (~A+~B). Закон работает аналогично в обратном направлении: ~(A+B) = (~A&~B)

Диаграмма Венна (иногда диаграмма Эйлера — Венна) — схематичное изображение всех возможных пересечений нескольких (часто — трёх) множеств.

Диаграммы Венна (как их ещё называют) изображают все   комбинаций   свойств, то есть конечную булеву алгебру. При  диаграмма Эйлера — Венна обычно изображается в виде трёх кругов с центрами в вершинах равностороннего треугольника и одинаковымрадиусом, приблизительно равным длине стороны треугольника.

Они появились в сочинениях английского логика Джона Венна (1834—1923), подробно изложившего их в книге «Символическая логика», изданной в Лондоне в 1881 году

Вопрос№8 Частично и вполне упорядоченные множества

Частично упорядоченное множество — математическое понятие, которое формализует интуитивные идеи упорядочения, расположения элементов в определённой последовательности. Неформально, множество частично упорядочено, если указано, какие элементы следуют за какими (какие элементы больше каких). В общем случае может оказаться так, что некоторые пары элементов не связаны отношением «следует за».

В качестве абстрактного примера можно привести совокупность подмножеств множества из трёх элементов   (булеан данного множества), упорядоченную по отношению включения.

Порядком, или частичным порядком, на множестве   называется бинарное отношение   на   (определяемое некоторым множеством  ), удовлетворяющее следующим условиям^[1]:

• Рефлексивность: 

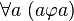
• Транзитивность: 

• Антисимметричность: 

Множество  , на котором задано отношение частичного порядка, называется частично упорядоченным (англ. partially ordered set, poset). Если быть совсем точным^[2], то частично упорядоченным множеством называется пара  , где   — множество, а   — отношение частичного порядка на  .

Вполне упорядоченное множество — линейно упорядоченное множество M такое, что в любом его непустом подмножестве есть наименьший элемент, другими словами, этофундированное множество с линейным порядком. Иными словами, это такое множество, элементы которого можно упорядочить, используя при этом знак < или >, но не знак равенства.

Множества типа {"первый элемент" < "следующий элемент" < ... < "последний элемент"} или {"первый элемент" > "следующий элемент" > ... > "последний элемент"} являются вполне упорядоченными, причем множества не обязательно должны быть конечными.

Конкретный пример: {2 < 3 < 5 < 6} = {2, 3, 5, 6}, {10 > 3 > 2 > 1} = {10, 3, 2, 1}

Те множества, для упорядочивания которых обойтись только одним знаком < или > нельзя, а требуется еще и знак =, называются частично упорядоченные(или в общем случае <= или >=).

Множества типа {"первый элемент" <= "следующий элемент" <= ... <= "последний элемент"} или {"первый элемент" >= "следующий элемент" >= ... >= "последний элемент"} являются частично упорядоченными, множества не обязательно должны быть конечными.

Конкретный пример критерия упорядочивания - воинское звание {солдат Петров <= солдат Иванов <= сержант Сидоров <= лейтенант Смирнов <= лейтенант Щеглов} = {солдат Петров = солдат Иванов < сержант Сидоров < лейтенант Смирнов = лейтенант Щеглов} = {солдат Петров, солдат Иванов, старший солдат Сидоров, лейтенант Смирнов, лейтенант Щеглов}. Из-за того, что во множестве присутствуют одинаковые по званию военные, приходится использовать знак равенства, множество является только частично упорядоченным.

Вопрос №9 Общие правила комбинаторики: закон перестановки, перемещения и правило сумм, произведения ( для 2-х множеств и общее)

Правило суммы: пусть имеется n попарно непересекающихся множеств A₁, A₂, …, A_n , содержащих m₁, m₂, …, m_n элементов соответственно. Число способов, которыми можно выбрать один элемент из всех этих множеств, равно m₁ + m₂ + … + m_n.

Пример. Если на первой полке стоит X книг, а на второй Y, то выбрать книгу с первой или второй полки, можно X+Y способами.

Правило произведения: пусть имеется n множеств A₁, A₂, …, A_n содержащих m₁, m₂, …, m_n элементов соответственно. Число способов, которыми можно выбрать по одному элементу из каждого множества, т. е. построить кортеж (а₁, а₂, ..., а_n), где а_i Î А _i1 (i = 1, 2, …, n), равно m₁ · m₂ · … · m_n.

Пример. Если на первой полке стоит 5 книг, а на второй 10, то выбрать одну книгу с первой полки и одну со второй можно 5*10=50 способами.

Размещениями из n элементов по m элементов (m < n) называются комбинации, составленные из данных n элементов по m элементов, которые отличаются либо самими элементами, либо порядком элементов.

Число размещений без повторений из n по m (n различных элементов) вычисляется по формуле:

(3.1)

Размещениями с повторениями из n элементов по m называются упорядоченные m-элементные выборки, в которых элементы могут повторяться.

Перестановки

Перестановками из n элементов называются размещения из этих n элементов по n (Перестановки - частный случай размещений).

Число перестановок без повторений (n различных элементов) вычисляется по формуле: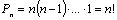

Число перестановок c повторениями (k различных элементов, где элементы могут повторяться m₁, m₂, …, m_k раз и m₁ + m₂ +… + m_k = n, где n - общее количество элементов) вычисляется по формуле:

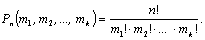
Сочетания

Сочетаниями из n элементов по m элементов называются комбинации, составленные из данных n элементов по m элементов, которые различаются хотя бы одним элементом (отличие сочетаний от размещений в том, что в сочетаниях не учитывается порядок элементов).

Число сочетаний без повторений (n различных элементов, взятых по m) вычисляется по формуле:

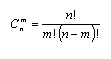
Число сочетаний c повторениями (n элементов, взятых по m, где элементы в наборе могут повторяться) вычисляется по формуле:

10 Вопрос делимость в кольце целых чисел

Определение 4.1. Пусть   и  целые числа,   Говорят, что число   делит число  , если существует такое целое число   что справедливо равенство   В этом случае число   называется делителем числа  , а число   частным от деления. При этом используют следующие обозначения:

 (  делит  )  или   (  делится на  ).

Замечание. Определение 4.1 задаёт в кольце целых чисел   отношение делимости.

Теорема 4.1. Пусть  целые числа. Справедливы следующие утверждения:

1) отношение делимости в кольце целых чисел рефлексивно, т. е. 

2) отношение делимости в кольце целых чисел транзитивно, т. е. если   и   то 

3) если   и   то 

4) 

5) 

6) если  , то 

7) если   и   то 

8) если  , то 

9) если   и   то 

10) если   и   то 

11) если   и   то 

12)   тогда и только тогда, когда 

12.Алгоритм Евклида (нахождение наибольшего общего делителя)

Алгоритм Евклида – это алгоритм нахождения наибольшего общего делителя (НОД) пары целых чисел. Наибольший общий делитель (НОД) – это число, которое делит без остатка два числа и делится само без остатка на любой другой делитель данных двух чисел. Проще говоря, это самое большое число, на которое можно без остатка разделить два числа, для которых ищется НОД.

Описание алгоритма нахождения нод делением

1. Большее число делим на меньшее.

2. Если делится без остатка, то меньшее число и есть НОД (следует выйти из цикла).

3. Если есть остаток, то большее число заменяем на остаток от деления.

4. Переходим к пункту 1.

Пример: Найти НОД для 30 и 18. 30/18 = 1 (остаток 12) 18/12 = 1 (остаток 6) 12/6 = 2 (остаток 0). Конец: НОД – это делитель. НОД (30, 18) = 6

13.Бином Ньютона

Возведение двучлена a + b в степень n может быть произведено по формуле называемой разложением бинома Ньютона:

(a + b)ⁿ = aⁿ + C¹_n a^{n - 1} b + C²_n a^{n - 2} b² +...+C^k_n a^{n - k} b^k +... + C^{n - 1}_n ab^{n - 1} + Cⁿ_nbⁿ

или (после подстановки выражений C^k_n с учетом формулы C^k_n = C^{n - k}_n):

,

где C^k_n — число всех возможных сочетаний, которые можно образовать из n элементов по k.

Пример: (a + b)⁵ = a⁵ + C¹₅ a⁴b + C²₅ a³b² + C³₅ a²b³ + C⁴₅ ab⁴ + C⁵₅ b⁵ = a⁵ + 5a⁴b + 10a³b² + 10a²b³ + 5ab⁴ + b⁵

Свойства бинома Ньютона

1. Разложение бинома (a + b)ⁿ представляет собой многочлен, расположенный по убывающим степеням a (от n-й до нулевой) и по возрастающим степеням b (от нулевой до n-й); сумма показателей a и b в каждом члене разложения равна показателю степени бинома. Число членов разложения на единицу больше показателя степени бинома.

2. Коэффициенты членов разложения («биноминальные коэффициенты») возрастают до середины разложения и затем убывают; коэффициенты каждой пары членов, равноотстоящих от начала и конца разложения, равны между собой. Если n четное, то имеется один средний наибольший коэффициент; если n нечетное, то имеется два средних наибольших коэффициента.

3. При возведении в n-ю степень разности a - b все четные члены разложения имеют знак "минус": 

14. Сравнения по модулю m.

(вкратце )

Числа а и b называют сравнимыми по модулю m,

если их разность делится на m

Т1.

Число а сравнимо с b по модулю m тогда и только тогда,

когда а и b имеют одинаковые остатки при делении на m

Т2. Рефлексивность отношения сравнимости.

Т3. Симметричность отношения сравнимости:

Т4. Транзитивность отношения сравнимости :

Т5. Если и k-произвольное целое число, то

Т8.

Т 9. К обеим частям сравнения можно прибавить или

вычесть одно и то же число

Т.13 В любой части сравнения можно отбросить или

добавить слагаемое, кратное модулю.

(По книжке Судоплавский)

16. Решения линейного уравнения no модулю m. Китайская теорема об остатках. Теорема: Уравнение ax ≡ b (mod m) тогда и только тогда имеет решение, когда (a, m)|b. Если решение существу­ет, то оно единственно по модулю m/d, где d = (a,m), и уравнение имеет d решений по модулю m. Следствие: Уравнение ax ≡ 1 (mod m) тогда и толь­ко тогда имеет решение, когда (a, m) = 1. Решение a^-1 (mod m) единственно по модулю m и является обратным к a элементом по модулю m. Китайская теорема об остатках: Пусть m₁, m₂,..., m_k— попарно взаимно простые целые числа больше 1, М = m₁m₂... m_k . Тогда существует единственное неотрицательное решение по модулю М следующей системы уравнений: х ≡ a₁ (mod m₁), х ≡ a₂ (mod m₂),..., х ≡ a_k (mod m_k). Отображение, которое каждому целому числу х (0 ≤ х ≤ М - 1) ставит в соответствие строку (a₁, a₂,..., a_k), где х ≡ a_i (mod m) (i = 1,2,...,k), является изоморфизмом кольца Z_M на Z_M1 х Z_M2 х ... Z_Mk.