26. Вероятностный смысл характеристик

Вероя́тность — степень (мера, количественная оценка) возможности наступления некоторого события. Когда основания для того, чтобы какое-нибудь возможное событие произошло в действительности, перевешивают противоположные основания, то это событие называют вероятным, в противном случае — невероятным или маловероятным. Перевес положительных оснований над отрицательными, и наоборот, может быть в различной степени, вследствие чего вероятность (и невероятность) бывает большей или меньшей^[1]. Поэтому часто вероятность оценивается на качественном уровне, особенно в тех случаях, когда более или менее точная количественная оценка невозможна или крайне затруднительна. Возможны различные градации «уровней» вероятности^[2].

27. Равномерное и показательное распределение

Равномерная.Непрерывная случайная величина  , принимающая значения на отрезке [a, b], распределена равномерно на [a, b], если ее плотность распределения p_ (x) и функция распределения F_x (x) имеют соответственно вид:

    ,  .

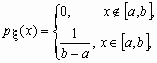
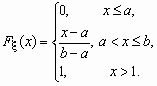
Показательное. Непрерывная случайная величина  имеет показательное распределение с параметром  > 0, если она принимает только неотрицательные значения, а ее плотность распределения p_ (x )и функция распределения F_ (x) имеют соответственно вид:

    ,  .

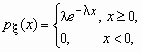
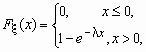
28. Нормальное распределение Гаусса

Нормальное распределение,^[1][2] также называемое распределением Гаусса — распределение вероятностей, которое в одномерном случае задается функцией плотности вероятности, совпадающей с функцией Гаусса:

где параметр μ — математическое ожидание, медиана и мода распределения, а параметр σ — стандартное отклонение (σ² — дисперсия) распределения.

Таким образом, одномерное нормальное распределение является двухпараметрическим семейством распределений. Многомерный случай описан в многомерном нормальном распределении.

Стандартным нормальным распределением называется нормальное распределение с математическим ожиданием μ = 0 и стандартным отклонением σ = 1.

29. Функции от случайных величин

Закон распределения вероятностей функции одной случайной величины

При решении задач, связанных с оценкой точности работы различных автоматических систем, точности производства отдельных элементов систем и др., часто приходится рассматривать функции одной или нескольких случайных величин. Такие функции также являются случайными величинами. Поэтому при решении задач необходимо знать законы распределения фигурирующих в задаче случайных величин. При этом обычно известны закон распределения системы случайных аргументов и функциональная зависимость.

Таким образом, возникает задача, которую можно сформулировать так.

Дана система случайных величин  , закон распределения которой известен. Рассматривается некоторая случайная величина Y как функция данных случайных величин:

(6.1)

Требуется определить закон распределения случайной величины  , зная вид функций (6.1) и закон совместного распределения ее аргументов.

Рассмотрим задачу о законе распределения функции одного случайного аргумента

Пусть   — дискретная случайная величина, имеющая ряд распределения

Тогда   также дискретная случайная величина с возможными значениями  . Если все значения   различны, то для каждого   события   и   тождественны. Следовательно,

и искомый ряд распределения имеет вид

Если же среди чисел   есть одинаковые, то каждой группе одинаковых значений   нужно отвести в таблице один столбец и соответствующие вероятности сложить.

Для непрерывных случайных величин задача ставится так: зная плотность распределения   случайной величины  , найти плотность распределения   случайной величины  . При решении поставленной задачи рассмотрим два случая.

Предположим сначала, что функция   является монотонно возрастающей, непрерывной и дифференцируемой на интервале  , на котором лежат все возможные значения величины  . Тогда обратная функция   существует, при этом являясь также монотонно возрастающей, непрерывной и дифференцируемой. В этом случае получаем

(6.2)