11. Теоремы умножения вероятностей

Вероятность произведения двух событий равна вер-ти одного из них, умноженной на условную вероятность другого при наличии первого:

Р (АВ) = Р(А) · Р(В/А), или Р (АВ) = Р(В) · Р(А/В).

Следствие. Вероятность совместного наступления двух независимых событий А и В равна произведению вероятностей этих событий:

Р (АВ) = Р(А) · Р(В).

Следствие. При производимых n одинаковых независимых испытаниях, в каждом из которых события А появляется с вероятностью р, вероятность появления события А хотя бы один раз равна 1 - (1 - р)n

12. Формула полной вероятности

Формула полной вероятности позволяет вычислить вероятность интересующего события через условные вероятности этого события в предположении неких гипотез, а также вероятностей этих гипотез.

Если событие А может произойти только при выполнении одного из событий , которые образуют полную группу несовместных событий, то вероятность события А вычисляется по формуле

.

13. Формула апостериорной вероятности Байеса.

 Пусть   — полная группа событий, и   — некоторое событие, вероятность которого положительна. Тогда условная вероятность того, что имело место событие  , если в результате эксперимента наблюдалось событие  , может быть вычислена по формуле:

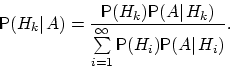
14. Повторение испытаний.

Формула Бернулли 

где   - вероятность появления события A ровно k раз при n независимых испытаниях; p - вероятность появления события A при каждом испытании.

     Вероятность того, что при этом событие A:

     1) наступит n раз:  ;

     2) не наступит ни разу:  ;

     3) наступит хотя бы один раз:  ;

     4) наступит не более k раз:  ;

     5) наступит не менее k раз:  .

ле:

16. Теорема Лапласа

 Пусть  A  – квадратная матрица  n-го порядка.        Определитель  k-го порядка, составленный из элементов матрицы  A, расположенных на пересечении строк с номерами  i₁ ,  i₂ , ...,  i_k  и столбцов с номерами  j₁ ,  j₂ , ...,  j_k , называется минором  M   k-го порядка матрицы  A.        Если из матрицы  A  вычеркнуть строки и столбцы с такими номерами, то определитель  n–k-го порядка полученной матрицы называется дополнительным минором для минора  M.        Обозначим символом  S  сумму индексов, нумерующих строки и столбцы такого минора:

S = i₁ + j₁ + i₂ + j₂ + ... + i_k + j_k .

      Алгебраическим дополнением минора  M  называется дополнительный минор для минора  M, умноженный на  (–1)^S.        Отметим, что алгебраическое дополнение  A_i j  элемента  a_i j  (минора первого порядка) является частным случаем алгебраического дополнения минора.  Теорема Лапласа. Пусть  D  – определитель  n-го порядка, в котором произвольно выбраны  k  строк (или столбцов), где  1 ≤k ≤ n – 1.  Тогда определитель  D  равен сумме произведений всех миноров  k-го порядка, расположенных в выбранных строках (или столбцах), на их алгебраические дополнения. 

17. Дискретные и непрерывные случайные величины.

В том случае, если случайное событие выражается в виде числа, можно говорить о случайной величине.Случайной называют величину, которая в результате испытания примет одно возможное значение, наперёд неизвестное и зависящее от случайных причин, которые заранее не могут быть учтены.

Выпадение некоторого значения случайной величины Х это случайное событие: Х = х_i. Среди случайных величин выделяют дискретные и непрерывные случайные величины.

Дискретной случайной величиной называется случайная величина, которая в результате испытания принимает отдельные значения с определёнными вероятностями. Число возможных значений дискретной случайной величины может быть конечным и бесконечным. Примеры дискретной случайной величины: запись показаний спидометра или измеренной температуры в конкретные моменты времени.

Непрерывной случайной величиной называют случайную величину, которая в результате испытания принимает все значения из некоторого числового промежутка. Число возможных значений непрерывной случайной величины бесконечно. Пример непрерывной случайной величины: измерение скорости перемещения любого вида транспорта или температуры в течение конкретного интервала времени.

Любая случайная величина имеет свой закон распределения вероятностей и свою функцию распределения вероятностей. Прежде, чем дать определение функции распределения, рассмотрим переменные, которые её определяют. Пусть задано некоторое х – действительное число и получена случайная величина X, при этом (x>X). Требуется определить вероятность того, что случайная величина Х будет меньше этого фиксированного значения х.

Функцией распределения случайной величины Х называется функция F(х), определяющая вероятность того, что случайная величина Х в результате испытания примет значение меньшее значения х, то есть:

F (х) = Р(Х < х ).

(5.1)

где х – произвольное действительное число.

Случайная величина (непрерывная или дискретная) имеет численные характеристики:

Математическое ожидание М (Х). Эту характеристику можно сравнивать со средним арифметическим наблюдаемых значений случайной величины Х.

Дисперсия D(X). Это характеристика отклонения случайной величины Х от математического ожидания.

Среднее квадратическое отклонение s(Х) для дискретной и непрерывной случайной величины Х – это корень квадратный из ее дисперсии:

.