50. Проверка пирсона

Критерий Пирсона

Критерий согласия  Пирсона позволяет осуществлять проверку эмпирического и теоретического (либо другого эмпирического) распределений одного признака. Данный критерий применяется, в основном, в двух случаях:

- Для сопоставления эмпирического распределения признака с теоретическим распределением (нормальным, показательным, равномерным либо каким-то иным законом);

- Для сопоставления двух эмпирических распределений одного и того же признака.

         Идея метода – определение степени расхождения соответствующих частот n_i и ; чем больше это расхождение, тем больше значение

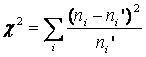
Объемы выборок должны быть не меньше 50 и необходимо равенство сумм частот

         Нулевая гипотеза H₀={два распределения практически не различаются между собой}; альтернативная гипотеза – H₁={расхождение между распределениями существенно}.

         Приведем схему применения  критерия для сопоставления двух эмпирических распределений:

51. Критерий Колмогорова-Смирнова

Данный критерий также позволяет оценить существенность различий между двумя выборками, в том числе возможно его применение для сравнения эмпирического распределения с теоретическим.

         Критерий позволяет найти точку, в которой сумма накопленных частот расхождений между двумя распределениями является наибольшей, и оценить достоверность этого расхождения. Нулевая гипотеза H₀={различия между двумя распределениями недостоверны (судя по точке максимального накопленного расхождения между ними)}.

52. Статистический анализ случайных процессов

Статистический анализ случайных процессов

        раздел математической статистики, посвященный методам обработки и использования статистических данных, касающихся случайных процессов (См.Случайный процесс) (т. е. функций X (t) времени t, определяемых с помощью некоторого испытания и при разных испытаниях могущих в зависимости от случая принимать различные значения). Значение x (t) случайного процесса X (t), получаемое в ходе одного испытания, называется реализацией (иначе — наблюдённым значением, выборочным значением или траекторией) процесса X (t); статистические данные о X (t), используемые при статистическом анализе этого процесса, обычно представляютсобой сведения о значениях одной или нескольких реализаций x (t) в течение определенного промежутка времени или же о значениях каких-либо величин, связанных с процессом X (t) (например, о наблюденных значениях процесса Y (t), являющегося суммой X (t) и некоторого «шума» N (t), созданного внешними помехами и ошибками измерения значений x (t)). Весьма важный с точки зрения приложений класс задач С. а. с. п. представляют собой задачи обнаружения сигнала на фоне шума, играющие большую роль при радиолокации. С математической точки зрения эти задачи сводятся к статистической проверке гипотез (См. Статистическая проверка гипотез): здесь по наблюденным значениям некоторой функции требуется заключить, справедлива ли гипотеза о том, что функция эта является реализацией суммы шума N (t) и интересующего наблюдателя сигнала X (t), или же справедлива гипотеза о том, что она является реализацией одного лишь шума N (t). В случаях, когда форма сигнала X (t) не является полностью известной, задачи обнаружения часто включают в себя и задачи статистической оценки (См. Статистические оценки) неизвестных параметров сигнала; так, например, в задачах радиолокации очень важна задача об оценке времени появления сигнала, определяющего расстояние до объекта, породившего этот сигнал. Задачи статистической оценки параметров возникают и тогда, когда по данным наблюдений за значениями процесса X (t) в течение определённого промежутка времени требуется оценить значения каких-то параметров распределения вероятностей случайных величин X (t) или же, например, оценить значение в фиксированный момент времени t = t₁ самого процесса Х (t) (в предположении, что t₁ лежит за пределами интервала наблюдений за этим процессом) или значение y (t₁) какого-либо вспомогательного процесса Y (t), статистически связанного с Х (t) (см. Случайных процессов прогнозирование). Наконец, ряд задач С. а. с. п. Относится к числу задач на Непараметрические методы статистики; так обстоит дело, в частности, когда по наблюдениям за течением процесса X (t) требуется оценить некоторые функции, характеризующие распределения вероятностей значений этого процесса (например, плотность вероятности величиныХ (t), или корреляционную функцию Ex (t) X (s) процесса Х (t), или, в случае стационарного случайного процесса (См. Стационарный случайный процесс) X (t), его спектральную плотность f (λ)