44. Числовые характеристики статистического распределения
В главе 5 мы ввели в рассмотрение различные числовые характеристики случайных величин: математическое ожидание, дисперсию, начальные и центральные моменты различных порядков. Эти числовые характеристики играют большую роль в теории вероятностей. Аналогичные числовые характеристики существуют и для статистических распределений. Каждой числовой характеристике случайной величины соответствует ее статистическая аналогия. Для основной характеристики положения — математического ожидания случайной величины – такой является среднее арифметическое наблюденных значений случайной величины:
,
(7.4.1)
где 
—
случайной величины, наблюденное 
-м
опыте, 
-
число опытов.
Эту характеристику мы будем в дальнейшем называть статистическим средним случайной величины.
Согласно закону больших чисел, при ограниченном увеличении числа опытов статистическое среднее приближается (сходится по вероятности) к математическому ожиданию. При ограниченном числе опытов статистическое среднее является случайной величиной, которая, тем не менее, связана с математическим ожиданием и может дать о нем известное представление.
Подобные статистические аналогии существуют для всех числовых характеристик. Условимся в дальнейшем эти статистические аналогии обозначать теми же буквами, что и соответствующие числовые характеристики, но и снабжать их значком *.
45. Точечные и интервальные оценки параметров распределения
Важной задачей математической статистики является задача оценивания (приближенного определения) по выборочным данным параметров закона распределения признака X генеральной совокупности. Другими словами, необходимо по данным выборочного распределения оценить неизвестные параметры теоретического распределения. Статистические оценки могут быть точечными и интервальными.
Задачу статистического оценивания, а также основные виды статистических оценок, рассмотрим для частного случая: пусть признак X генеральной совокупности распределен нормально, то есть теоретическое распределение имеет вид:
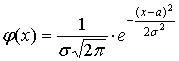
с
параметрами: 
–
математическое ожидание признака X ; 
–
среднеквадратическое отклонение
признака X.
Точечной оценкой неизвестного параметра называют число (точку на числовой оси), которое приблизительно равно оцениваемому параметру и может заменить его с достаточной степенью точности в статистических расчетах.
Точечной
оценкой генеральной средней 
и
параметра a может служить выборочная
средняя 
.
Точечными
оценками генеральной дисперсии 
могут
служить выборочная дисперсия 
,
или, при малых объемах выборки n ,
исправленная выборочная дисперсия:
.
Точечными
оценками для генерального
среднеквадратического отклонения 
могут
служить: 
–
выборочное среднее квадратическое
отклонение или 
–
исправленное выборочное среднее
квадратическое отклонение.
Формулы, необходимые для вычисления выборочной средней и выборочной дисперсии , приведены в п. 2.
Для того чтобы точечные статистические оценки обеспечивали “хорошие” приближения неизвестных параметров, они должны быть несмещенными, состоятельными и эффективными.
Для
построения интервальной оценки рассмотрим
событие, заключающееся в том, что
отклонение точечной оценки параметра 
от
истинного значения этого параметра q
по абсолютной величине не превышает
некоторую положительную величину D .
Вероятность такого события 
.
Заменив неравенство 
на
равносильное, получим:
.
Вероятность
того, что доверительный интервал 
заключает
в себе (покрывает) неизвестный параметр
q равна g и называется доверительной
вероятностью или надежностью интервальной
оценки. Величину D называют точностью
оценки.