42. Статистический ряд

Вариационным (статистическим) рядом называется таблица, первая строка которой содержит в порядке возрастания элементы  ', а вторая - их частоты   (относительные частоты  .

В математической статистике исследуются утверждения, которые могут быть сделаны на основе измерения некоторой величины, на простейшем примере поясним постановку (одной из многих) задач математической статистики.

Пусть требуется измерить некоторую величину  . Результаты измерений

естественно рассматривать как значения случайных величин  , полученных в данном эксперименте. Если измерительный инструмент не имеет систематической ошибки, то можно положить  . Следовательно, возникает задача оценить параметр  . Для решения задачи рассмотрим случайную величину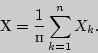 Тогда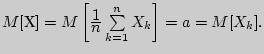 

Это обстоятельство приводит к мысли построить статистические характеристики:

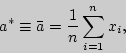
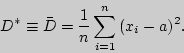
Первая представляет среднее арифметическое наблюденных значений случайной величины   и статистическую дисперсию - во втором случае. В соответствии с законом больших чисел эти среднеарифметические сходятся по вероятности соответственно к математическому ожиданию величины   и к дисперсии

При ограниченности наблюдений эксперимента заменой   и   на   и   совершаем погрешность, а при небольшом числе наблюдений величины   ,   являются случайными величинами. Возникает задача об оценке неизвестных параметров  ,   случайной величины   на основе экспериментальных данных, т.е. задача - найти подходящие значения этих параметров.

Множество результатов измерений   величины   называется выборкой объема  . Для того, чтобы иметь возможность воспользоваться аппаратом теории вероятностей, целесообразно наблюдаемую величину   рассматривать как случайную величину, функцию распределения которой следует определить.

Полученный статистический материал  ,  , ...  наблюдений представляет собой первичные данные о величине, подлежащей статистической обработке. Обычно такие статистические данные оформляются в виде таблицы, графика, гистограммы и т.д. Если выборка объема   содержит   различных элементов  , причем   встречается   раз, то число   называется частотой элемента  , а отношение   называетсяотносительной частотой элемента  . Очевидно, что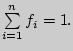 

43. Статистические оценки параметров распределения

След. »

Пусть дискретная случайная величина Х задана генеральной совокупностью. Требуется оценить количественные характеристики заданной совокупности: математическое ожидание, дисперсию и установить функцию распределения дискретной случайной величины Х. Обычно практически известны лишь данные выборки. Через эти данные следует оценить количественные характеристики дискретной случайной величины Х. Статистической оценкой неизвестного параметра теоретического распределения называют функцию от наблюдаемых случайных величин.  Статистические оценки параметров распределения должны удовлетворять следующим требованиям: состоятельности, несмещённости, эффективности. Состоятельной называют статистическую оценку, которая при неограниченном увеличении числа наблюдений стремится по вероятности к оцениваемому параметру. Несмещённой называют статистическую оценку, если её математическое ожидание равно оцениваемой характеристике независимо от числа наблюдений. Несмещённая статистическая оценка называется эффективной, если она имеет минимально возможную дисперсию. Генеральная средняя и выборочная средняя Пусть задана дискретная случайная величина Х в виде генеральной совокупности. Генеральной средней называют среднее арифметическое значений признака генеральной совокупности:   . (6.2) где xi – варианта генеральной совокупности, ni – частота варианты xi, . N– все возможные значения частот дискретной случайной величины Х. В частном случае, когда генеральная совокупность содержит по одному значению каждой варианты, генеральная средняя равна:   . (6.2а) Если рассматривать значения Х генеральной совокупности как случайную величину, то математическое ожидание М(Х) равно генеральной средней М(Х)= xг, а генеральная средняя определяется как математическое ожидание: xг = М(Х). Пусть извлечена выборка объема n из генеральной совокупности относительно количественного признака X. Выборочной средней`x называется среднее арифметическое значение признака выборочной совокупности.   , (6.3) где .
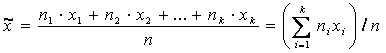