Часть 2

Лабораторная работа 7

СОЗДАНИЕ ЭКСПЕРТНОЙ СИСТЕМЫ В MATLAB.

АЛГОРИТМ МАМДАНИ

Общие сведения

Используемый в различного рода экспертных системах механизм нечетких выводов в своей основе имеет базу знаний, формируемую специалистами предметной области в виде совокупности нечетких предикатных правил вида:

П₁: если х есть А₁, то у есть В₁,

П₂: если х есть А₂, то у есть В₂,

………………………………………….

П_n: если х есть А_n, то у есть В_n .

Общий логический вывод осуществляется за следующие 4 этапа:

1. Нечеткость.

Функции принадлежности, определенные на входных переменных, применяются к их фактическим значениям для определения степени истинности каждой предпосылки каждого правила.

2. Логический вывод.

Вычисленное значение истинности для предпосылок каждого правила применяется к заключениям каждого правила. Это приводит к одному нечеткому подмножеству, которое будет назначено каждой переменной вывода для каждого правила. В качестве правил логического вывода обычно используются только операции min (МИНИМУМ) или prod (УМНОЖЕНИЕ). В логическом выводе МИНИМУМА функция принадлежности вывода «отсекается» по высоте, соответствующей истинной степени истинности предпосылки правила (нечеткая логика «И»). В логическом выводе УМНОЖЕНИЯ функция принадлежности вывода масштабируется при помощи вычисленной степени истинности предпосылки правила.

3. Композиция.

Все нечеткие подмножества, назначенные для каждой переменной вывода, объединяются вместе, чтобы формировать одно нечеткое подмножество для каждой переменной вывода. При подобном объединении обычно используются операции max (МАКСИМУМ) или sum (СУММА). При композиции МАКСИМУМА комбинированный вывод нечеткого подмножества конструируется как поточечный максимум по всем нечетким подмножествам (нечеткая логика «ИЛИ»). При композиции СУММЫ комбинированный вывод нечеткого подмножества конструируется как поточечная сумма по всем нечетким подмножествам, назначенным переменной вывода правилами логического вывода.

4. Приведение к четности (дефазификация).

Используется, когда нужно преобразовать нечеткий набор выводов в четкое число.

Алгоритм Мамдани.

Данный алгоритм математически может быть описан следующим образом. Для простоты будем считать, что базу знаний образуют два нечетких правила:

П₁: если х есть А₁ и у есть В₁, то z есть C₁,

П₂: если х есть А₂ и у есть В₂, то z есть C₂.

1. Нечеткость: находятся степени истинности для предпосылки каждого правила А₁(х₀), А₂(х₀), В₁(y₀), В₂(y₀).

2. Нечеткий вывод: находятся уровни отсечения для предпосылок каждого из правил с использованием операции МИНИМУМ:

₁ = А₁(х₀)  В₁(у₀),

₂ = А₂(х₀)  В₂(у₀),

где через  обозначена операция логического минимума (min), затем находятся «усеченные» функции принадлежности

С₁(z) = (₁  C₁(z)),

С₂(z) = (₂  C₂(z)).

3. Композиция: с использованием операции МАКСИМУМ (max, обозначение: ) производится объединение найденных усеченных функций, что приводит к получению итогового нечеткого подмножества для переменной выхода с функцией принадлежности

_(z) = C(z) = C₁(z)  C₂(z) = (₁  C₁(z))  (₂  C₂(z)).

4. Приведение к четкости (для нахождения z₀) проводится, например, центроидным методом (как х – координата центра тяжести функции принадлежности итогового нечеткого подмножества для переменной выхода).

Создание ЭС в MatLab

Для простоты будем считать, что базу знаний образуют два нечетких правила:

П₁: если х есть А₁ и у есть В₁, то z есть C₁,

П₂: если х есть А₂ и у есть В₂, то z есть C₂.

Создадим в MatLab экспертную систему:

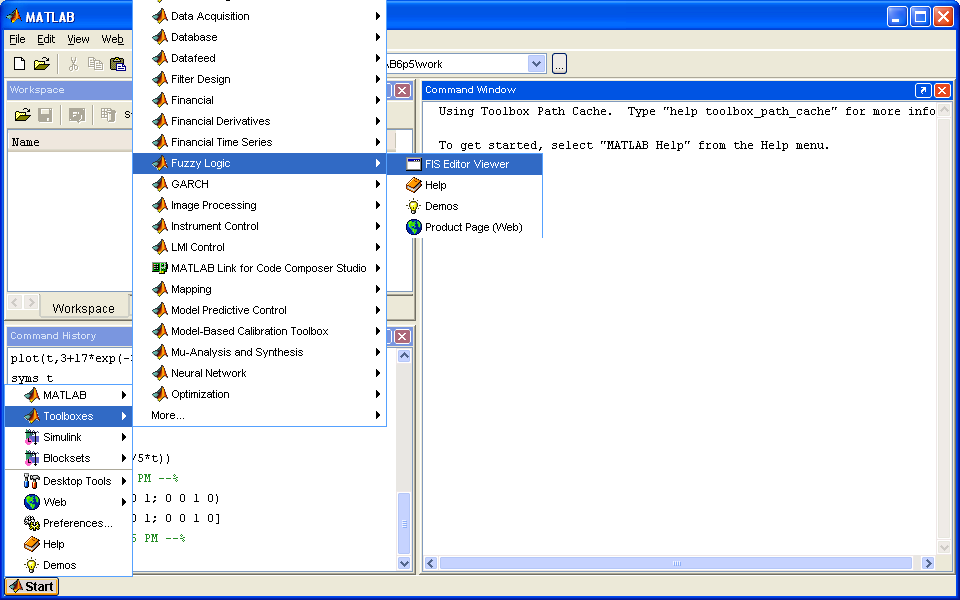
В открывшемся окне выбираем Edit  FIS properties. Открывается окно FIS Editor:

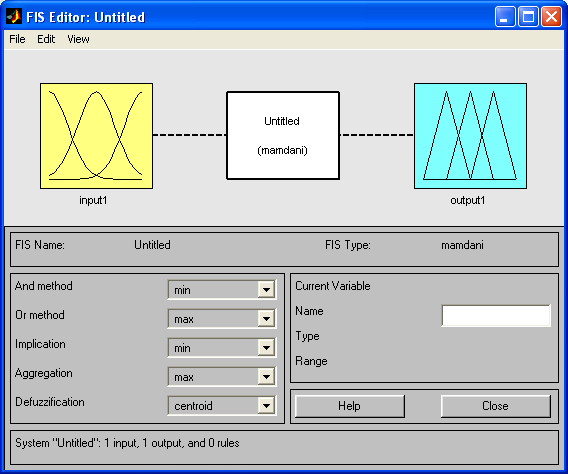
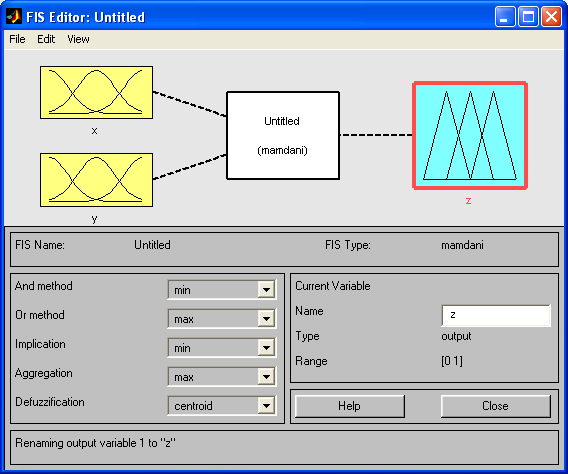
Задаем две входные переменные x и y (EditAdd VariableInput) и одну выходную переменную z (EditAdd VariableOutput). Окно принимает вид:

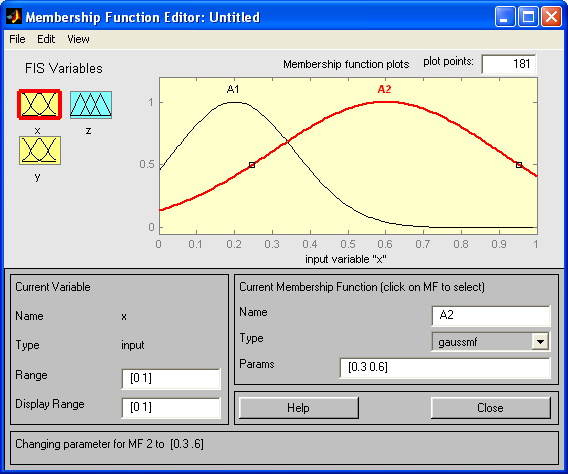
Для переменной x, щелкнув на соответствующей иконке, задаем две гауссовых функции принадлежности (А₁ и А₂) (параметры выбрать произвольно):

Для переменной y, щелкнув на соответствующей иконке, задаем две гауссовых функции принадлежности (B₁ и B₂) (параметры выбрать произвольно).

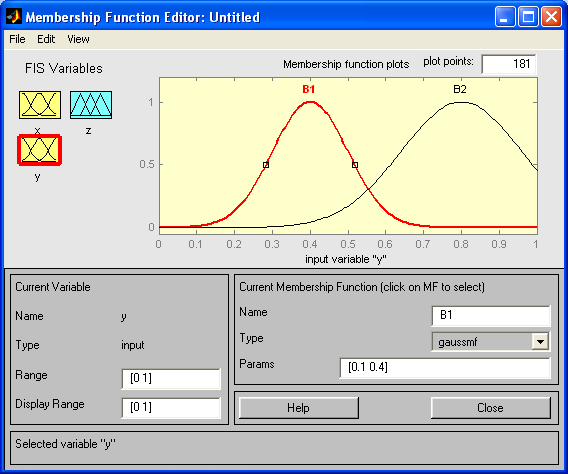
Для переменной z, щелкнув на соответствующей иконке, задаем две треугольных функции принадлежности (C₁ и C₂) (параметры выбрать произвольно).

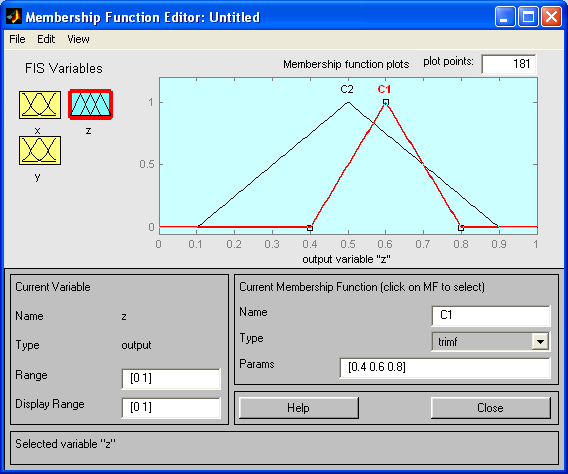
Открываем окно задания правил (Edit  Rules) и задаем два правила, устанавливая переключатели и нажимая кнопку Add Rule:

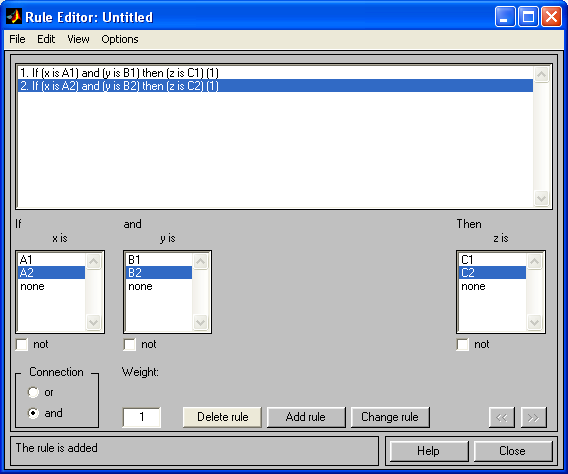
Для демонстрации работы экспертной системы выбираем View Rules:

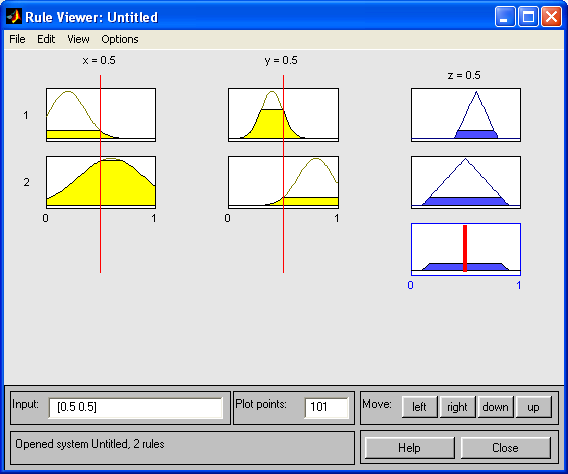
Задание.

1. Изменяя значения входных переменных, наблюдать за процессами композиции и дефуззификации.

2. Получить трехмерный график зависимости значений выходной переменной от значений входных переменных (View  Surface).

3. Получить двумерный график зависимости значений выходной переменной от значений одной входной переменной при фиксированной другой (выбрать, например, значение переменной y none).