Лабораторная работа 3 Вычислительный эксперимент, программирование, разработка приложений

Выполнение команд, содержащихся в M-файле, осуществляется двумя способами:

1. Из редактора M-файлов (клавиша F5).

2. Из командной строки или другого M-файла, при этом в качестве команды используется имя M-файла.

Первый способ рекомендуется при отладке программы. Применение второго способа намного удобнее, особенно, если созданный M-файл будет неоднократно использоваться впоследствии. Закройте все окна и наберите в командной строке fun2. Появится графическое окно с результатом.

П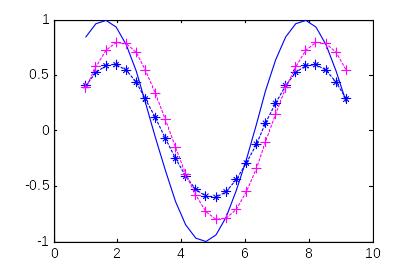 ример 1. Программа для построения рис. 13 записана в M-файл с именем graf1.m. Для интервала исследования >>x=1: pi/10: 3*pi; graf1(x) получен график (рис. 15).

function y=graf1(x)

y=sin(x);

y2=0.6*sin(x-0.25);

y3=0.8*sin(x-0.5);

plot(x,y, x,y2, 'b:*', x,y3, 'm:+')

Рис. 15

Пример 2. Программа для построения рис. 12 записана в M-файл с именем graf.m. Причем интервал исследования для переменной теперь стал входным параметром программы:

function y=graf(x)

title('{\itf(x)=x^{n}}');

xlabel('x');

ylabel('y');

hFigure=gcf;

set(hFigure,'Color',[1 1 1]);

hText=text;

set(hText,'FontSize',[18]);

for n=2:4

y=x.^n;

hold on

hPlot=plot(x,y);

set(hPlot,'Color',[1.8/n 0.7 0.5]);

set(hPlot,'LineWidth',2);

if n~=2

for i=1:length(y)

s='';

if y(i)==y1(i)

hold on

plot(x(i),y(i),'ko');

s=['(' num2str(x(i)) ',' num2str(y(i)) ')'];

hText=text(x(i),y(i)+2, s); set(hText,'FontSize',[16]);

end

end

end

y1=y; s2=['n=' num2str(n)];

hText=text(1.5, 1.5^2*n-1, s2); set(hText,'FontSize',[14]);

end

Теперь можно построить график функции в другом интервале изменения параметра x. После выполнения команды x=-3: 0.1: 2.5; graf(x) построен график (рис. 15).

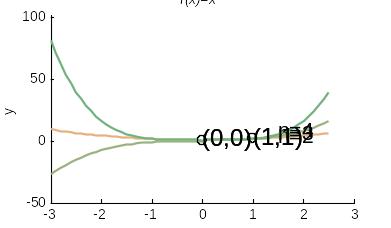
Рис. 15

Лабораторная работа 4 Кинематика процесса копания грунта поворотом ковша экскаватора

Объем грунта, вырезаемый рабочим органом за один цикл в плотном теле, определяется из выражения

V = 0,5R²l_к(2  sin). (1)

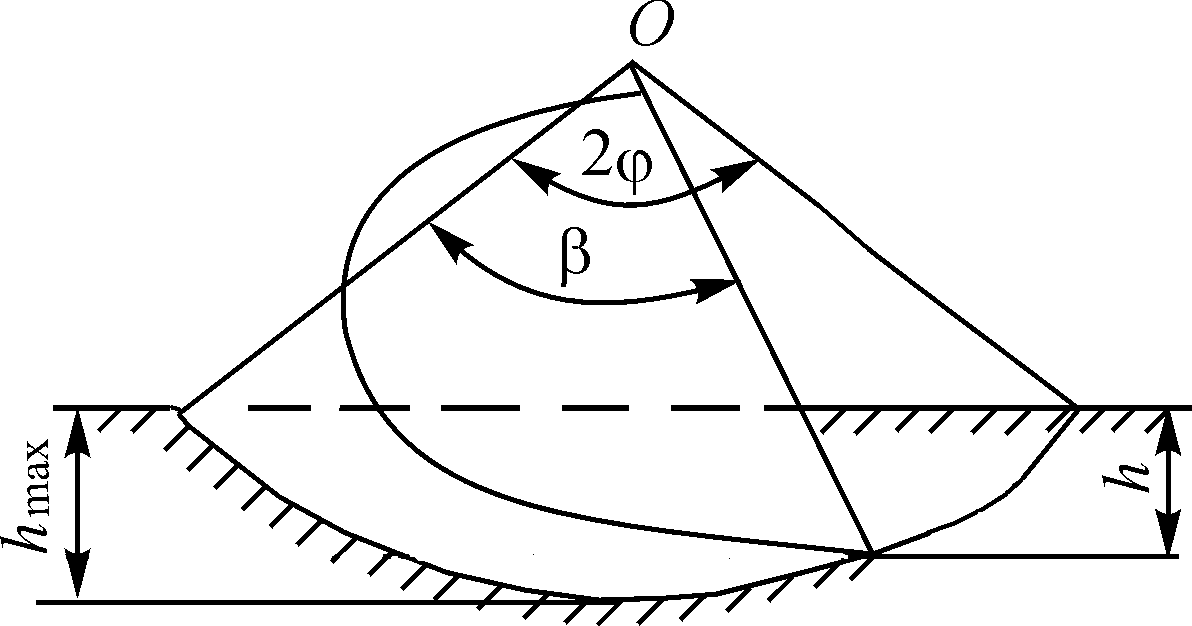
Рис. 16. Схема копания грунта поворотным движением ковша

Глубина резания на начальном этапе

h = R[cos(  )  cos], (2)

где h – глубина резания, м; R – радиус резания, м;  – половина полного угла поворота ковша в грунте, град;  – текущий угол поворота ковша, определяющий положение ковша относительно принятой системы отсчета, град.

При копании поворотом ковша R = R_к, при копании поворотом рукояти с ковшом R = R_к + l_р, где R_к – радиус ковша; l_р – длина рукояти.

Полагая, что весь разработанный грунт окажется в ковше: V = q, где q – вместимость ковша. Тогда угол поворота ковша , необходимый для полного наполнения ковша определяется из формулы:

(2  sin) = .

Угол  может быть определен только приближенно. Зададим точность его определения величиной 0,0002. М-файл (если точнее, М-функция F.m) дает определение  при копании поворотом рукояти и ковша.

function [FIK,FIR]=F(q, lr)

lk=1.51*q^0.333-0.26;

RK=1.3*(q+0.3)^0.333;

R=lr+RK;

KNAP=1; KRAZR=1;

a2K=2*q*KNAP/(KRAZR*lk*RK^2);

a2R=2*q*KNAP/(KRAZR*lk*(RK+lr)^2); FIK=0; FIR=0;

for f=0.1: 1E-4: 1.4

a1=2*f-sin(2*f);

if abs(a2K-a1)<= 2E-4

FIK=f;

end

if abs(a2R-a1)<= 0.5E-4

FIR=f;

end

end

if FIK==0 | FIR==0

disp([' УГОЛ FI НЕ ОПРЕДЕЛЕН в бдоке FI'])

end

f=FIK; z1=2*f-sin(2*f);

f=FIR; z2=2*f-sin(2*f);

f=0.1: 0.01: 1.4;

a1=2*f-sin(2*f);

plot(f,a1, f,z1,'b:*', f,z2, 'm:+')

После вызова М-функции FI.m командой

>> q =0.4; lr = 1.6; [FIK,FIR]=F(q,lr);

будет построен график (рис. 17).

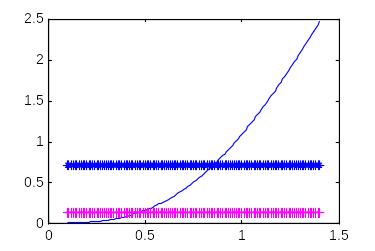
Рис. 17