Розділ 5. Лінійні електричні кола несинусоїдного струму

5.1. Несинусоїдні струми та напруги

Синхронні генератори електричних станцій, які є джерелами електричної енергії, конструюються так, що ЕРС, індуковані в обмотках статора, змінюються за синусоїдним законом. Внаслідок цього лінійні напруги силової трифазної мережі змінюються в часі практично теж за законом синуса.

О днак, іноді криві зміни напруг та струмів мають форму, відмінну від синусоїди. Причиною цього можуть бути недосконала побудова генератора, що дає несинусоїдну ЕРС, та нелінійність елементів електричних кіл. Несинусоїдна ЕРС генератора може визначатись несинусоїдним розподілом магнітної індукції обертового магнітного поля в повітряному проміжку між ротором і статором та нелінійністю магнітного кола синхронної машини внаслідок насичення. Нелінійні елементи (котушки з феромагнітними осердями, вентильні пристрої тощо) зумовлюють спотворення форми кривих струмів і напруг через нелінійність зв'язку між ними. На рис. 5.1 наведено приклади періодичних несинусоїдних струмів у нелінійній індуктивній котушці за відсутності гістерезису (рис. 5.1, а) та у вітці з керованим вентилем - тиристором (рис. 5.1, б). Отже, періодичними несинусоїдними струмами та напругами називають такі струми та напруги, які змінюються в часі за періодичним несинусоїдним законом.

Несинусоїдні періодичні функції задовільняють умову , де Т – період функції, п = 0, 1, 2, 3... – ціле число. В цьому посібнику розглядається методика розрахунку й особливості роботи лінійних електричних кіл при дії на них несинусоїдних ЕРС та струмів.

5.2. Розкладання періодичних функцій у ряд Фур’є

Аналіз електричних кіл несинусоїдних струмів грунтується на розкладан­ні періодичних несинусоїдних ЕРС, струмів та напруг у ряд Фур'є. Як відомо з курсу математики, будь-яка періодична функція , що відповідає умовам Діріхле (має протягом періоду скінченну кількість розривів першого роду та скінченну кількість максимумів та мінімумів), може бути розкладена в ряд Фур'є:

(5.1)

Змінна х з часом t пов'язана таким співвідношенням:

Тут період функції в радіанній мірі дорівнює , а період цієї ж функції за часом дорівнює Т.

Складову ряду (5.1) називають сталою складовою, або нульовою гармонікою; величини – відповідно амплітуди синусних і косинусних складових k-x гармонік.

Амплітуди обчислюються за такими формулами:

(5.2)

Оскільки

де і , (5.3)

то ряд Фур'є (5.1) можна записати в такому вигляді:

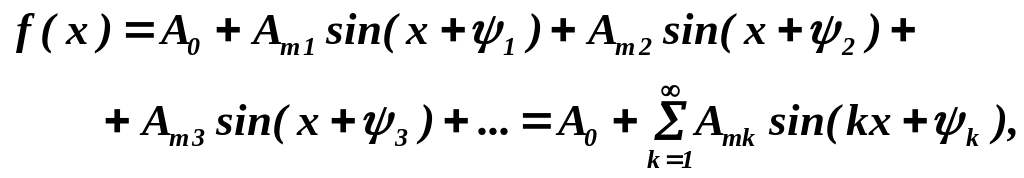(5.4)

або, замінивши х на , згідно з (5.1) одержимо:

(5.5)

Складову ряду (5.1) називають основною хвилею чи першою (основною) гармонікою; решту складових для – вищими гармоніками.

5.3. Властивості симетричних періодичних кривих

5.3.1. Криві, для яких виконується умова

,

називаються симетричними відносно осі абсцис. Якщо від’ємну півхвилю такої кривої (рис. 5.2) зсунути по осі абсцис на півперіоду й дзеркально відобразити відносно осі х, то одержимо криву, яка буде збігатися з . Подібними кривими описуються струми нелінійних індуктивних котушок та струми біполярно увімкнених транзисторів. При розкладі такої кривої в ряд Фур'є не буде сталої складової та парних гармонік, а ряд матиме вигляд:

(5.6)

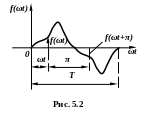
5.3.2. Криві, для яких виконується умова , мають симет­рію відносно початку координат (рис. 5.3). Розкладання їх в ряд Фур'є має такий вигляд:

(5.7)

5.3.3. Криві для яких виконується умова , мають симетрію відносно осі ординат (рис. 5.4). Прикладом такої кривої є напруга двопівперіодного випрямлення. При розкладі такої кривої в ряд Фур’є відсутні синусні складові, а ряд має вигляд:

(5.8)