Раздел 7. Функции многих переменных. Ряды.

Глава 1. Функции двух переменных. Основные определения. Приращения функции.

Пусть на плоскости ХY задана область D. Каждой точке М этой области соответсвует упорядоченная пара чисел (х, у) - ее координаты.

Если каждой упорядоченной паре чисел (х, у) поставлено в соответствие по закону f число z, то говорят, что задана функция двух переменных

z = f (x, у) (1.1)

Область D называется областью определения функции. Множество Z ={z} образует область значений функции. График функции f(x,y) - поверхность в пространстве (рис 1.1), эту поверхность часто обозначают σ. Проекция поверхности σ на плоскость XOY и есть область D.

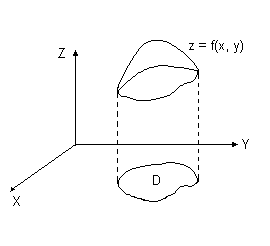
Рис.1.1. Функция двух переменных.

Функция двух переменных может быть также задана в виде таблиц.

Аналогично задается функция трех и более переменных. Физически, например, функцию трех переменных u = f(x,y,z,) можно интерпретировать как плотность вещества в объемной области D.

Следует заметить, что функции двух переменных являются самым простым и наглядным случаем среди всех функций многих переменных и поэтому обычно подробно рассматриваются. Полученные при этом свойства остаются верными и для функций произвольного числа переменных.

Если на оси Z нанести масштаб, и провести через точки деления плоскости, перпендикулярные оси Z, то поверхность σ разделится на части. На каждой линии сеченияповерхности σ плоскостью функция z = f (x, у) будет постоянной величиной. Линии сечения проектируют на плоскость ХY и называют линиями уровня (рис. 1.2).

Рис. 1.2. Линии уровня.

Функция z = f (x, у) называется непрерывной в точке М₀(x₀, y₀), если имеет место равенство

и точка М(x, y) стремится к М₀(x₀, y₀) оставаясь все время в области определения функции. Функция непрерывная в каждой точке области называется непрерывной во всей области.

Если функция непрерывна в ограниченной замкнутой области, то она достигает там своего наименьшего m и наибольшего M значений.

Приращения функции двух переменных.Выберем в области определения функции точку М₀ с координатами x₀ и y₀ т.е. М₀(x₀, y₀) и точку М₁ с координатами x₁ и y₁ М₁(x₁, y₁) (рис.3). вычислим в этих точках значения функции z₀ = f(x₀, у₀) и z₁ = f(x₁, у₁) .

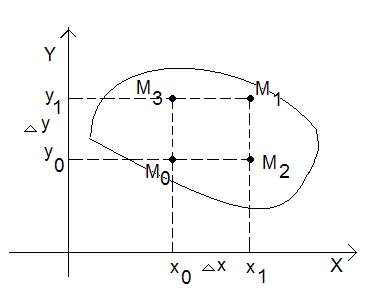
Рис. 1.3. Приращения функции двух переменных

Полным приращением функции двух переменных Δz называется разность ее значений в точках М₁ и М₀

. (1.2)

Сделаем дополнительное построение. Построим точку М₂(x₁, y₀) и М₃(x₀, y₁). Частным приращением по аргументу х Δ_хz называется разность значений функции в точках М₂ и М₀

, (1.3)

а частным приращением по аргументу у Δ_уz называется разность значений функции в точках М₃ и М₀

. (1.4)

Сумма частных приращений, в общем случае, не совпадает с полным приращением.

Глава 2. Частные производные

Частной производной от функции двух переменных f(x,y) по переменной х при y = y₀ называется предел, при Δх стремящемся к нулю, отношения частного по х приращения функци к вызвавшему его приращению аргумента Δх (если этот предел существует и конечен). Так как y₀ любое фиксированное число из области допустимых значений, то его можно заменить на просто у. Тогда

Частная производная от функции f(x,y) по переменной y определяется и обозначается аналогичным образом

То есть, при вычислении частной производной от функции двух переменных f(x,y) по х второй аргумент y выступает как величина постоянная. Если же вычисляется частная производная по y, то х принимается постоянной величиной.

Пример 1. Вычислить частные производные z_x и z_y от функции

f(x,y) = x³y² + sin x - 4y.

Решение. В соответствии с определением, имеем

f_x(x,y) = 3x²y² + cos x и f_y(x,y) = 2x³y - 4.

Частная производная от f(x,y) тоже является функцией двух переменных и от нее вновь можно вычислять частные производные и так далее.

Функция двух переменных имеет следующие вторые производные:

• вторая производная от f(x,y) по х дважды

• вторая производная от f(x,y) по y дважды

• вторая смешанная производная от f(x,y) по x и по y

- вторая смешанная производная от f(x,y) по y и по х.

для функций, имеющих непрерывные частные производные второго порядка, смешанные производные второго порядка совпадают

Пример 2 (продолжение примера 1). Вычислить вторые производные для функции

f(x,y) = x³y² + sin x - 4y.

Решение. Применяя правила дифференцирования, получим

z_xx = (3x²y² + cos x)_х’ = 6xy² - sin x,

z_yy = (2x³y – 4)_y’ = 2x³,

z_xy = (3x²y² + cos x)_y’ = 6x²y = z_yx.

Теперь не представляет труда решение задачи о вычислении производных любого порядка.

Пример 3. Вычислить четвертую производную, причем одну по х и три по y для функции

f(x,y) = 2x⁴ ּ lny - cos(x + y³) + x³

В соответствии и правилами дифференцирования сложных функций и функций многих переменных имеем:

Производные от функций большего числа производных вычисляются по тем же правилам.

Пример 4. Пусть дана функция четырех переменных f(x,y,z,t)

f(x,y,z,t) = xz³t² + yz² cos(y³ - t).

Решение. Вычислим вторую смешанную производную по аргументам z и t