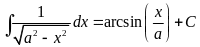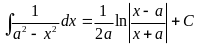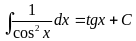- •Раздел 5. Первообразная и неопределенный интеграл
- •Глава 1. Определение первообразной. Свойства первообразной.
- •Глава 2. Определение неопределенного интеграла. Свойства неопределенного интеграла.
- •Глава 3. Методы интегрирования
- •Раздел 6. Определенный интеграл
- •Глава 1. Площадь криволинейной трапеции.
- •Глава 2. Определение определенного интеграла. Свойства определенного интеграла.
- •Глава 3. Вычисление определенного интеграла
- •Глава 5. Приложения определенного интеграла
- •Глава 6. Несобственные интегралы
- •Раздел 7. Функции многих переменных. Ряды.
- •Глава 1. Функции двух переменных. Основные определения. Приращения функции.
- •Глава 2. Частные производные
- •Глава 3. Дифференциалы функции двух переменных
- •Глава 4. Градиент и производная по направлению.
- •Глава 5. Экстремум функции двух переменных
- •Глава 6. Метод наименьших квадратов.
- •Глава 7. Числовые ряды.
- •Глава 8. Степенные ряды
- •Раздел 8. Дифференциальные уравнения
- •Глава 1. Основные понятия теории дифференциальных уравнений
- •Глава 2. Дифференциальные уравнения первого порядка
- •Глава 3. Линейные дифференциальные уравнения второго порядка
- •191028, Санкт-Петербург, ул. Моховая, 26
|
|||||||||
|
|
||||||||
|
|
||||||||
УДК 512.64 + 514.74 +517(075.8)
ББК 22.143.+ 22.151+ 22.161я73 ISBN 978-5-7973-0834-0 ISBN 978-5-7973-0836-7 © ФГБОУВПО «СПГУТД», 2013 © Мещерякова Г. П., 2013
|
|
||||||||
Введение
Учебное пособие содержит теоретический материал и примеры по следующим разделам курса математики: Часть 1. Линейная и векторная алгебра. Геометрия на плоскости и в пространстве. Введение в анализ. Дифференциальное исчисление функции одной переменной.
Часть 2.интегральное исчисление. Основные понятия теории функций двух переменных. Дифференциальные уравнения. Последовательности и ряды. Такое деление на части соответствует делению на семестры двух семестрового курса математики. В некоторых программах предусматривается несколько иное расположение разделов – «Теория функций двух переменных» предшествует разделу «Интегралы». Такая перестановка вполне допустима и не мешает изучению курса. Пособие содержит большое число примеров, что облегчает понимание теоретического материала и удобно при выполнении контрольных работ студентами безотрывных форм обучения. Пособие может быть использовано и при самостоятельной работе студентов и при работе с преподавателем в аудитории.
|
|
||||||||
Раздел 5. Первообразная и неопределенный интеграл
Глава 1. Определение первообразной. Свойства первообразной.
Операция нахождение производной от функции называется дифференцированием. Обратная дифференцированию операция - отыскание функции по ее производной называется интегрированием.
Функция F(x), производная которой равна функции f(x), т.е.
F(x) = f(x) (1.1)
называется первообразной для f(x).
Так,
например, если f(x)
= xn,
то ее первообразная есть F(x)
=
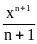 ,
так как
,
так как
 .
.
Tсли же f(x) = sin (2x), то ее первообразная
F(x) = - 0.5 cos(2x),
так как
 .
.
Теорема. Пусть F1(x) и F2(x) две первообразные одной и той же функции f(x) на промежутке [a,b]. Тогда разность между ними есть постоянная величина С.
Доказательство. Обозначим за Ф(х) разность между F2(x) и F1(x), т.е. Ф(х) = F2(x) - F1(x) и возьмем производную от функции Ф(х)
 (1.2)
(1.2)
Единственной функцией, производная которой при любом значении х равна нулю, есть постоянная величина, следовательно Ф(х) = const ≡ C и
F2(x) = F1(x) + С. (1.3)
Константа С называется постоянной интегрирования.
Пример.
Функция F(x)
= – 0.5 cos(2x)
является первообразной не только для
f(x)
= sin(2x), но и для f(x)
= sin(2x) + 4, и для f(x)
= sin(2x) -
 ,
и вообще для любой функции вида sin(2x) + C
,
и вообще для любой функции вида sin(2x) + C
Следствие. Функция f(x) имеет бесконечное множество первообразных {F(x)}вида
F(x) + C, отличающихся на постоянную величину.
Глава 2. Определение неопределенного интеграла. Свойства неопределенного интеграла.
Множество всех первообразных функции f(x) называется неопределенным интегралом от этой функции и обозначается так
 ,
(2.1)
,
(2.1)
где - знак интеграла, читается “интеграл”,
f(x) - подынтегральная функция от переменной интегрирования х,
f(x)dx - подынтегральное выражение,
C - постоянная интегрирования.
Часто вместо слов "вычислить неопределенный интеграл" говорят "взять неопределенный интеграл".
Из определения интеграла следует, что
Производная от неопределенного интеграла равна подинтегральной функции. Действительно
 (
( )
= (F(x)
+ C) =
F (x)
+ 0 = f(x).
(2.2)
)
= (F(x)
+ C) =
F (x)
+ 0 = f(x).
(2.2)
Дифференциал от неопределенного интеграла равен подинтегральному выражению. Действительно, так как dF = F (x)dx, получим
d( ) = ( )dx = f(x)dx. (2.3)
Интеграл от дифференциала первообразной равен самой первообразной. Действительно, пусть F(x) - первообразная для функции f(x) ( т.е. F(x) = f(x)). Тогда
 F(x)dx
=
= F(x)
+ C (2.4)
F(x)dx
=
= F(x)
+ C (2.4)
или
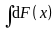 =
F(x) + C
(2.5)
=
F(x) + C
(2.5)
Формулы (2.2 – 2.5) наглядно иллюстрируют то обстоятельство, что операции дифференцирования и интегрирования взаимно обратны с точностью до постоянной. В этой связи по аналогии с таблицей формул дифференцирования элементарных функций можно построить таблицу основных интегралов.
Справедливость этих формул проверяется по формуле (1.1) непосредственным дифференцированием.
Линейные свойства неопределенного интеграла.
Постоянный множитель можно выносить за знак неопределенного интеграла.
 (2.6)
(2.6)
Действительно, возьмем производную от левой и правой частей равенства по формуле (2.2) и проверим, что они совпадают, а это означает, что оба выражения есть первообразные одной и той же функции (1.2).

 .
.
Таблица основных интегралов
|
|
|
|
|
|
|
|
|
|
|
|
Неопределенный интеграл от суммы функций равен сумме неопределенных интегралов от этих функций.
 (2.7)
(2.7)
Доказательство аналогично.Действительно, возьмем производные от левой и правой части и проверим, что они совпадают. По формуле (2.2)
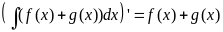

Замечание. Если каждый из суммируемых неопределенных интегралов содержит свою постоянную интегрирования, то для всей суммы записывается одна постоянная интегрирования.
Пример.
Найти
 .
.
Решение.Запишем стоящую в числителе единицу в тригонометрическом виде (1 = sin2x + cos2x) и разделим почленно числитель на знаменатель, получим табличные интегралы:

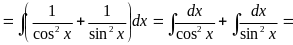


 013
013