21. Решение задачи Коши для дифференциальных уравнений методом Эйлера.
Метод Эйлера
Этот метод является простейшим численным методом решения задачи Коши.
Рассмотрим его на примере решения обыкновенного дифференциального уравнения первого порядка y′ = dy(t)/dt = f (y, t)
с соответствующим начальным условием
y0 = y(t 0 )
Заменим приращение в выражении (10.1) дифференциал dt на малое, но конечное приращение ∆t = h. Тогда соответствующее ему приращение ∆y будет равно:
∆y =h · f (t, y).
Используя начальное условие, получаем новое значение y:
y1 = y0 + ∆y = y0 + h · f (t0 , y0).
Распространяя этот подход на последующие шаги решения, получим конечно разностную формулу численного решения задачи Коши в виде:
y i+1 = y i + h · f (t i , y i).
Эта формула известна как формула метода Эйлера (часто ее называют явным методом Эйлера). Здесь (см. рис.) положение новой точки определяется по наклону кривой, вычисленному с помощью производной в данной точке. Таким образом, график численного решения представляет собой последовательность коротких прямолинейных отрезков, которыми аппроксимируется истинная кривая y = y(x). Сам численный метод определяет порядок действий при переходе от данной точки к следующей.
Отметим, что данную формулу можно получить, используя разложение функции y(t) в ряд Тейлора в окрестности некоторой точки ti с последующим отбрасыванием всех членов с дифференциалами высших порядков за исключением первого. Соответственно, использование данного подхода приводит к ошибке
аппроксимации, порядок которой соответствует Rn (h2).
Несмотря на достаточно большую погрешность данного метода, его простота в сочетании с физической и математической прозрачностью обусловили его широкое применение на практике. Кроме того на базе этого метода легче понять алгоритмы функционирования более сложных методов.
В настоящее время этот метод используется при решении ряда физических задач, для которых погрешность порядка долей процента и даже нескольких процентов в ряде случаев является приемлемой. Это позволяет решать данным методом многие физические задачи достаточно просто и наглядно, попросту выбирая приемлемый для данной задачи шаг h.
Модифицированный метод Эйлера
В рассмотренном явном методе Эйлера для снижения погрешности расчетов требуется уменьшение величины шага интегрирования h, что приводит к увеличению процесса решения задачи (иначе времени интегрирования).
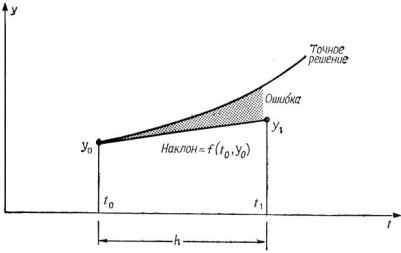
Хотя тангенс наклона касательной к истинной кривой в исходной точке известен и равен y′(t 0 ), он изменяется в соответствии с изменением независимой переменной. Поэтому в точке t 0 + h наклон касательной уже те таков, каким он был в точке t 0 . Следовательно, при сохранении начального наклона касательной во всем интервале h в результаты вычислений вносится погрешность (см. рис.). Точность метода Эйлера можно существенно повысить, улучшив алгоритм аппроксимации производной. Это можно сделать, например, используя среднее значение производной в начале и конце интервала. Именно это положено в основу модифицированного метода Эйлера (неявного метода Эйлера), алгоритм которого включает выполнение следующих шагов (см. рис 2)
1. Сначала вычисляется значение функции в следующей точке по явному методу Эйлера:
y’n+1 = y n + h·f(t n , y n ) ,
2. Полученное значение используется для приближенного вычисления производной в конце интервала f(t n+1, y’n+1).
3. Вычисляется среднее значение производной между ее значениями в начале и конце интервала с последующей подстановкой ее в обычную формулу Эйлера для получения более точного значения y n+1
y n+1 = y n + h·[f(t n , y n ) + f(t n+1 , y’n+1 )]/2 .
