17. Формулы приближенного дифференцирования, основанные на первой интерполяционной формуле Ньютона.

Пусть имеем функцию  , заданную в равноотстоящих точках   отрезка   с помощью

значений  .

Для нахождения на   производных  ,   и т. д. функцию   приближенно заменим

интерполяционным полиномом Ньютона, построенным для системы узлов  .

Имеем:

где   и  .

Производя перемножение биномов, получим:

Так как   

то

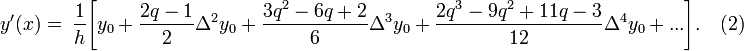
Аналогично, так как 

то

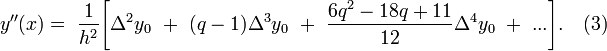
Таким же способом можно вычислить производные функции   любого порядка

При нахождении производных   в фиксированной точке   в качестве   выбирают ближайшие табличные значения аргумента.

В том случае, если необходимо найти производные функции   в основных табличных точках  , то полагают  , следовательно   и получают:

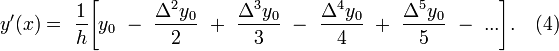
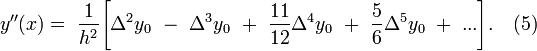
Формулы   применяют, для начальных строк таблицы. Для последних строк таблицы используют формулы получающиеся при дифференцировании второй интерполяционной формулы Ньютона

Если   - интерполяционный полином Ньютона, содержащий разности   и

Известно что:

где ξ - некоторое промежуточное значение между узлами интерполирования  и рассматриваемой

точной  . Поэтому, полагая, что  , получим:

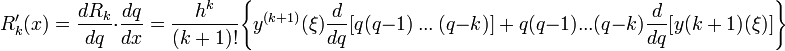
Отсюда при   и, следовательно, при   и учитывая,

что  ? ,будем иметь:

.

Так как   во многих случаях трудно оценить, то при <\math>\ h</math> малом приближенно полагают:

и, следовательно,

.

Аналогично может быть найдена погрешность   для второй производной 

18. . Формула прямоугольников. Формула трапеций. Оценки погрешности.

Формула трапеций

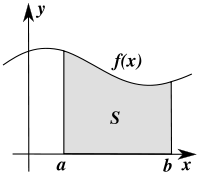
Определённый интеграл как площадь фигуры

Численное интегрирование (историческое название: квадратура) — вычисление значения определённого интеграла (как правило, приближённое), основанное на том, что величина интеграла численно равна площади криволинейной трапеции, ограниченной осью абсцисс, графиком интегрируемой функции и отрезками прямых   и  ,

где   и   — пределы интегрирования (см. рисунок).

Необходимость применения численного интегрирования чаще всего может быть вызвана отсутствием у первообразной функции представления в элементарных функциях и, следовательно, невозможностью аналитического вычисления значения определённого интеграла по формуле Ньютона-Лейбница. Также возможна ситуация, когда вид первообразной настолько сложен, что быстрее вычислить значение интеграла численным методом.

Одномерный случай

Основная идея большинства методов численного интегрирования состоит в замене подынтегральной функции на более простую, интеграл от которой легко вычисляется аналитически. При этом для оценки значения интеграла получаются формулы вида

где   — число точек, в которых вычисляется значение подынтегральной функции. Точки   называются узлами метода, числа   — весами узлов. При замене подынтегральной функции на полином нулевой, первой и второй степени получаются соответственно методы прямоугольников, трапеций и парабол(Симпсона). Часто формулы для оценки значения интеграла называют квадратурными формулами.

Метод прямоугольников

Пусть требуется определить значение интеграла функции на отрезке  . Этот отрезок делится точками   на   равных отрезков длиной   Обозначим через   значение функции   в точках   Далее составляем суммы   Каждая из сумм — интегральная сумма для   на   и поэтому приближённо выражает интеграл

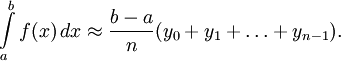
Если заданная функция — положительная и возрастающая, то эта формула выражает площадь ступенчатой фигуры, составленной из «входящих» прямоугольников, а формула

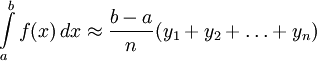
выражает площадь ступенчатой фигуры, состоящей из «выходящих» прямоугольников.

Чем меньше длина отрезков, на которые делится отрезок  , тем точнее значение, вычисляемое по этой формуле, искомого интеграла.

Погрешность

погрешность метода определяется величиной

которую легко оценить с помощью формулы Тейлора. Действительно, запишем   в виде

( 6 )

Обозначая  , оценим   следующим образом:

Таким образом, для погрешности формулы прямоугольников на частичном отрезке справедлива оценка

( 7 )

т.е. формула имеет погрешность   при  .

Заметим, что оценка (7) является не улучшаемой, т.е. существует функция  , для которой (7) выполняется со знаком равенства. Действительно, для   имеем   и

Метод трапеций

Если функцию на каждом из частичных отрезков аппроксимировать прямой, проходящей через конечные значения, то получим метод трапеций.

Площадь трапеции на каждом отрезке:

Погрешность аппроксимации на каждом отрезке:

 где 

Полная формула трапеций в случае деления всего промежутка интегрирования на отрезки одинаковой длины h:

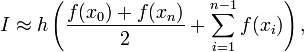 где 

Погрешность формулы трапеций:

 где